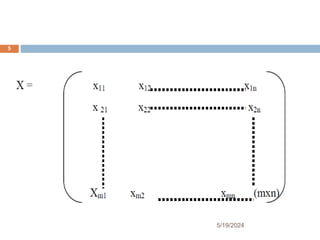
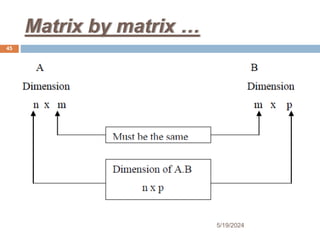
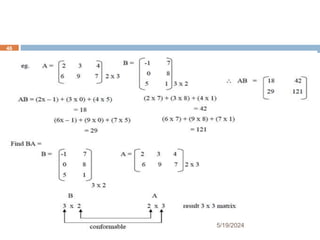
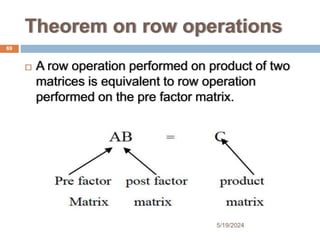
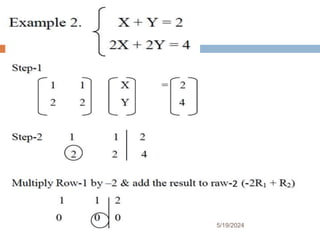
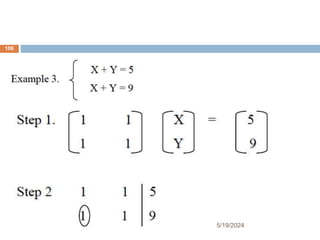
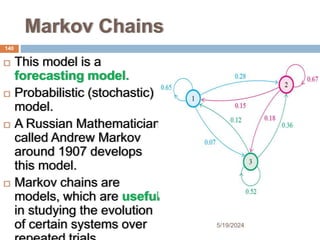
Chapter two focuses on matrices and their applications, starting with matrix concepts including definitions, dimensions, and various types like vectors and identity matrices. It covers fundamental matrix operations, properties, and the concept of matrix multiplication, including scalar and matrix products. The section concludes with the inverse of a matrix, detailing when it exists and methods for finding it using row operations.