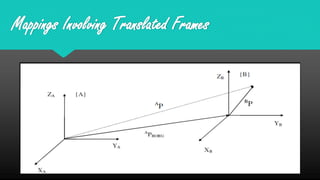
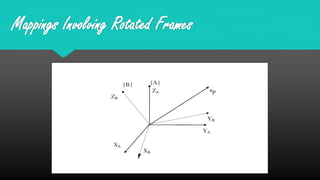
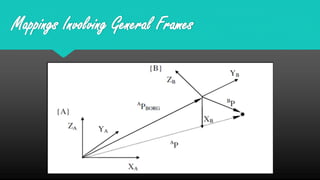
Mapping between frames refers to changing the description of a point or vector from one coordinate frame to another. There are three possibilities for how the second frame relates to the first: rotated, translated, or both rotated and translated. Translations involve moving the origin of one frame relative to the other while keeping the axes parallel. Rotations involve changing the orientation of one frame relative to the other while keeping the origins coincident. A general mapping involves both a rotation and a translation, which can be represented by a composite transformation matrix that performs the rotation followed by the translation. Homogeneous transformation matrices are also used to describe both the position and orientation of frames in space.

1. Mapping between frames
&
Description of objects in
space
Hitesh Mohapatra
https://www.linkedin.com/in/hiteshmohapatra/

2. What is Mapping?
 Mapping refers to changing the description of a point (or vector) in space from one
frame to another frame. The second frame has three possibilities in relation to the first
frame, viz.,
a) Second frame is rotated w.r.t. the first, the origin of both the frames is same.
b) Second frame is moved away from the first, the axes of both the frames remain
parallel, respectively.
c) Second frame is rotated w.r.t. the first and moved away from it, i.e., the second
frame is translated and its orientation is also changed.
 These situations are modelled in the following sections. It is important to note that
mapping changes the description of the point and not the point itself.

3. Mappings Involving Translated Frames
 We have a position defined by the vector B
P (a point P described in coordinate frame
{B}).
 We have to express this point in space in terms of coordinate frame {A}, when {A} has
the same orientation as {B}.
 In this case, {B} differs from {A} only by a translation which is given by A
PBORG (a
vector which locates the origin of {B} relative to {A}).
 The description of point P, B
P, relative to coordinate frame {A}, A
P, is determined by
simple vector addition, i.e.,
A
P = B
P + A
PBORG

4. Mappings Involving Translated Frames
 Alternatively, the description of point P, B
P, relative to coordinate frame {A}, A
P, can
also be determined by using a simple transformation matrix, i.e.,
A
P = T.B
P
 Where, T is the Translation Matrix which is given by
T =
1 0 0 𝑡𝑥
0 1 0 𝑡𝑦
0 0 1 𝑡𝑧
0 0 0 1

5. Mappings Involving Translated Frames

6. Mappings Involving Rotated Frames
 The origins of the two coordinate frames {A} and {B} are coincident but they have a
different orientation (rotated by a certain angle).
 The description of a point P in coordinate frame {B}, B
P, relative to coordinate frame
{A}, A
P, can be determined by using a simple transformation matrix, i.e.,
A
P = R.B
P
 Where, R is the Rotation Matrix which is given by
R =
𝑐𝑜𝑠α −𝑠𝑖𝑛α 0 0
−𝑠𝑖𝑛α 𝑐𝑜𝑠α 0 0
0 0 1 0
0 0 0 1
−𝑠𝑖𝑛γ 0 𝑐𝑜𝑠γ 0
0 1 0 0
𝑐𝑜𝑠γ 0 𝑠𝑖𝑛γ 0
0 0 0 1
1 0 0 0
0 𝑐𝑜𝑠β −𝑠𝑖𝑛β 0
0 𝑠𝑖𝑛β 𝑐𝑜𝑠β 0
0 0 0 1

7. Mappings Involving Rotated Frames
Where, R(𝜶) =
R(𝜷) =
R(𝜸) =
𝑐𝑜𝑠α −𝑠𝑖𝑛α 0 0
−𝑠𝑖𝑛α 𝑐𝑜𝑠α 0 0
0 0 1 0
0 0 0 1
−𝑠𝑖𝑛γ 0 𝑐𝑜𝑠γ 0
0 1 0 0
𝑐𝑜𝑠γ 0 𝑠𝑖𝑛γ 0
0 0 0 1
1 0 0 0
0 𝑐𝑜𝑠β −𝑠𝑖𝑛β 0
0 𝑠𝑖𝑛β 𝑐𝑜𝑠β 0
0 0 0 1
Thus,
R = R(𝜸).R(𝜷).R(𝜶)

8. Mappings Involving Rotated Frames

9. Mappings Involving General Frames
 We will explain the mapping involving general frames by taking the origin of frame
{B}, located at a distance of vector called A
PBORG from frame {A}; and {A} is rotated
with respect to {B} as described by R.
 The following equation describes the mapping of a vector from its description in one
frame to a description in a second frame, which is given by
A
P = R.B
P + A
PBORG
 The above equation can also be implemented in a matrix form by using a composite
transformation matrix, i.e.,
A
P = C.B
P

10. Mappings Involving General Frames
 Where, C is the Composite Transformation Matrix which is given by
C = R.T = R(𝜸).R(𝜷).R(𝜶).T
 So,
C =
 Thus,
A
P = R.T.B
P = R(𝜸).R(𝜷).R(𝜶).T .B
P
𝑐𝑜𝑠α −𝑠𝑖𝑛α 0 0
−𝑠𝑖𝑛α 𝑐𝑜𝑠α 0 0
0 0 1 0
0 0 0 1
−𝑠𝑖𝑛γ 0 𝑐𝑜𝑠γ 0
0 1 0 0
𝑐𝑜𝑠γ 0 𝑠𝑖𝑛γ 0
0 0 0 1
1 0 0 0
0 𝑐𝑜𝑠β −𝑠𝑖𝑛β 0
0 𝑠𝑖𝑛β 𝑐𝑜𝑠β 0
0 0 0 1
1 0 0 𝑡𝑥
0 1 0 𝑡𝑦
0 0 1 𝑡𝑧
0 0 0 1

11. Mappings Involving General Frames

12. Homogeneous Transformation Matrix
 Homogenous Transformation matrix is used to describe both the position and the
orientation of co-ordinate frames in space.
 Homogenous Transformation matrix is a 4 x 4 matrix that maps an object defined in
a homogeneous coordinate system and can be thought of as two sub-matrices, i.e. a
Translation matrix and a Rotation matrix.
 We can think of a Homogenous Transformation matrix as a Composite
Transformation matrix (refer to the 10th slide) in a homogeneous coordinate system.

13. Thank
You