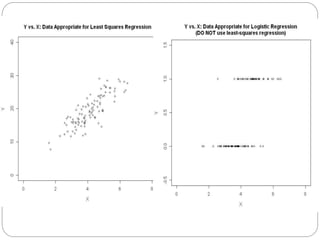
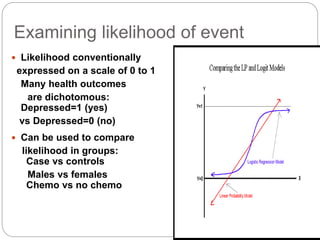
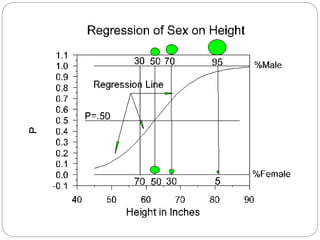
Logistic regression predicts the probability of a categorical outcome (usually dichotomous) based on one or more predictor variables. It transforms the probability into odds using the logit function and estimates coefficients using maximum likelihood estimation. The odds ratio describes the change in odds of the outcome occurring given a one-unit increase in the predictor, while controlling for other predictors. Logistic regression allows examination of the effects of variables on the relationship between the dichotomous outcome and predictors.

1. DV: categorical (dichotomous )
Exploring Relationships
 Is a variable related to the proportions of another?
 The first step is to examine the data using crosstabs
 Chi square test
 Logistic regression relies on an estimation procedure
 Models the probability of an outcome
 Transforms the probability of an event occurring into its
odds
 In logistic regression the regression coefficient (b) can
be interpreted as the change in the log odds associated
with a one-unit increase change in the associate
predictor variable.
ln[Y/(1−Y)]=a + bX

3. Multiple Regression Logistic
Regression
LOGIT
 Used to make predictions
about an unknown event
from known evidence
 DV continuous
 IV can be any level of
measurement
 Assumes linear
relationship
 Uses least squares
estimation
(computed coefficients that minimized
the residuals for all cases)
 Normally distributed
variables
 Equal variance
 Used to determine which
variables affect the
probability of a particular
outcome
 DV categorical
 IV may be any level of
measurement
 Doesn’t assume linear
relationship but rather a
logit transformation
 Uses maximum
likelihood estimation
(when the dependent variable is not
normally distributed, ML estimates
are preferred to OLS estimates
because they are unbiased )
 Doesn’t assume normal
distribution, or equal
variance
 Less stringent

4. DV: categorical
The Odds Ratio
Prob (event)
Prob (not event)
= e
b
0
+ b
1
x
The left hand side of the equation is the odds:
where the e is the base of the natural log.
What this equation tells us is that the e, raised to the power of, say
x1, is the factor by which the odds change when x1 increases by
one unit,
controlling for the other variables in the equation.
When the coefficient is positive, the odds increase;
when the coefficient is negative, the odds decrease.
b
0
+ b
1
x
1
+ b
2
x
2
+ b
3
x
3
+ …..
= e
Crude OR –simple logistic regression
Adjusted OR-
multiple logistic regression

5. Examining likelihood of event
 Likelihood conventionally
expressed on a scale of 0 to 1
Many health outcomes
are dichotomous:
Depressed=1 (yes)
vs Depressed=0 (no)
 Can be used to compare
likelihood in groups:
Case vs controls
Males vs females
Chemo vs no chemo

6. What logistic regression predicts
 probability of Y occurring given known values for X(s).
 In LR the DV is transformed into the natural log of the odds. This is
called logit (short for logistic probability unit).
 Probabilities ranged between 0.0 and 1.0 are
transformed into odds ratios that range between 0 and
infinity.
 If the probability for group membership in the modeled
category is above some cut point (the default is 0.50), the
subject is predicted to be a member of the modeled group.
If the probability is below the cut point, the subject is
predicted to be a member of the other group.
 For any given case, logistic regression computes the
probability that a case with a particular set of values for the
independent variable is a member of the modeled
category.

8. Logistic Regression
 Logistic regression estimates the probability of a
certain event occurring using the odds ratio by
calculating the logarithm of the odds
 Uses Maximum likelihood estimation (MLE) to
transform the probability of an event occurring into
its odds, a nonlinear model
 Odds ratio is the probability of occurrence of a
particular event over the probability of non
occurrence
 Odds ratio is useful in providing an estimate of the
magnitude of the relationship between binary
variables
 Allows one to examine the effects of the variables
on the relationship- how y varies when x varies

9. model fit
 The probability of the observed results, given the
parameter estimates, are used to determine how
well the estimated model fits the data
 Likelihood index: If the model fits perfectly, the –
2LL, will equal 0. Goodness-of-fit statistic (similar to
the F test in multiple regression) takes into consideration the
difference between the observed probability of an
event and the predicted probability—chi square
distribution.
 Hosmer Lemeshow test (based on Chi Square)
compares prediction to “perfect model”. When not
significant, the null hypothesis that the model fits is
supported, ie a non significant result indicates

10.  R2 values quantify the proportion of the variance
explained by the model
 In logistic regression the Nagelkerke statistic is used
to estimate the Psuedo R squared, which is the
magnitude of the relationship between the dependent
variable and the set of independent variables in the
model.
 The b-weights and constant associated with each IV are
used in Logistic regression to determine the probability of a
subject doing one thing or the other
 Instead of a score as with continuous variables, a
probability ranging from 0 –1 is given. If the probability is
greater than .05, the prediction is for the occurrence and if
less than .05 for non occurrence
 Signs of the b-wgts show direction of relationship