大阪 PRML 勉強会使用スライド

1. 機械学習
-chapter 7
最小二乗学習に基づく分類 -
Ryo HIGASHIAGWA
@biwakonbu

2. 前回課題
●
課題内容 : リッジ回帰
●
ガウスカーネル法の適用を選択
リッジ回帰ってなんだっけ ?
雑音に強くした最小二乗学習

3. 前回の課題
‖ x−c‖
K (x ,c)=exp(
)
2
2h
2

4. 前回の課題
repmat → 行列の繰り返し配置
...
m
や
.
.
.
n

5. 前回課題
phi → ガウスカーネルの値
y→
訓練標本
b→
単位行列のサイズ

6. 前回課題

7. 前回課題

8. 最小二乗学習に基づく分類
●
最小二乗分類
●
2 クラス分類問題
●
+1 と -1 の二値での判定
●
0 にはならない物とする
+ 1 f θ ( x )> 0
^
y
^ =sign ( f θ ( x ))={ 0 f ^ ( x )=0 }
^
θ
−1 f θ ( x )<0
^

9. 最小二乗学習に基づく分類
+1
sign(f θ (x))
f θ (x)
x1
x2
xn
−1

10. 分類問題での損失
●
クラス分けでは二値のみで関数の値は細かく見ない
●
本質的には 0/1 の判断のみ
●
+1/-1 と 0 が挟まるより自然
0/1 損失

11. 0/1 損失
1
(1−sign( f θ ( x) y))
2
0 と 1 にしかならない式
sign(x) は符号化関数なので +1/-1 しか無い

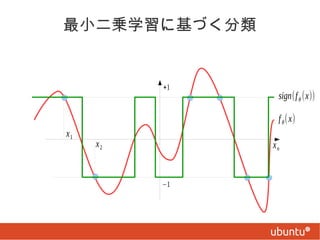
12. 0/1 損失最小化学習
n
1
min ∑ (1− sign ( f θ ( x i ) y i ))
2 i=1
θ
2
n
解の組み合わせが 存在する為
直接解く事が困難
また、傾きが無いため θ の最適解を一意に取れない

13. 代理損失
●
0/1 では考え方は自然だが不便
●
代理損失 ( 代わりの損失 ) を使用する
●
結局 l2 損失を用いる ( 今回の話 )

14. 最小二乗学習による分類
●
男女比 1 : 1 のデータ群から男女の分類を行った
●
データの種類
●
身長
●
体重
●
性別
ガウスカーネルモデルに対する l2 制約付き最小二乗化学習

15. 分類
y → +1/-1 の分類用標本、入力は 3 種類
b → a*x+b の b を出す為に使用 ( バイアス値 )

16. 分類
T
k
yk ( x)=w x +w k 0
y1 ( x)= y2 ( x)
クラスは二つの為、
k に 1,2 が入る

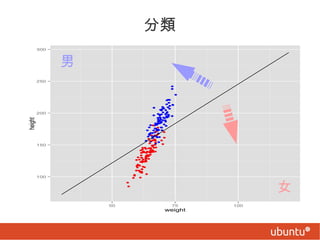
17. 分類
w 10 +w 11 x1 +w 12 x 2=w 20 +w 21 x 1+w 22 x2
w 11−w 21
w 10−w 20
x 2=−
x1−
w 12−w 22
w 12−w 22
R の場合
Wi は
11,12,13
21,22,23
となる

18. 分類
男
女

19. 分類まとめ
●
ニクラス分類は出来た
●
傾き等の最適解を学習により適切に出せなかった
●
フィッシャーの線形判別を用いる事で出来るらしい
●
関係無いけどガウスカーネル段々覚えてきました

20. 課題
●
今回同様のクラス分けを使い、 Python でインタラク
ティブなクラス分けを行うプログラムを作成する
●
男女のクラス分けの場合、あらかじめ学習させておき、
身長体重を入力するとクラスを提示する等
●
男女データは github にあげておくので使用する場合は取
得して使ってください