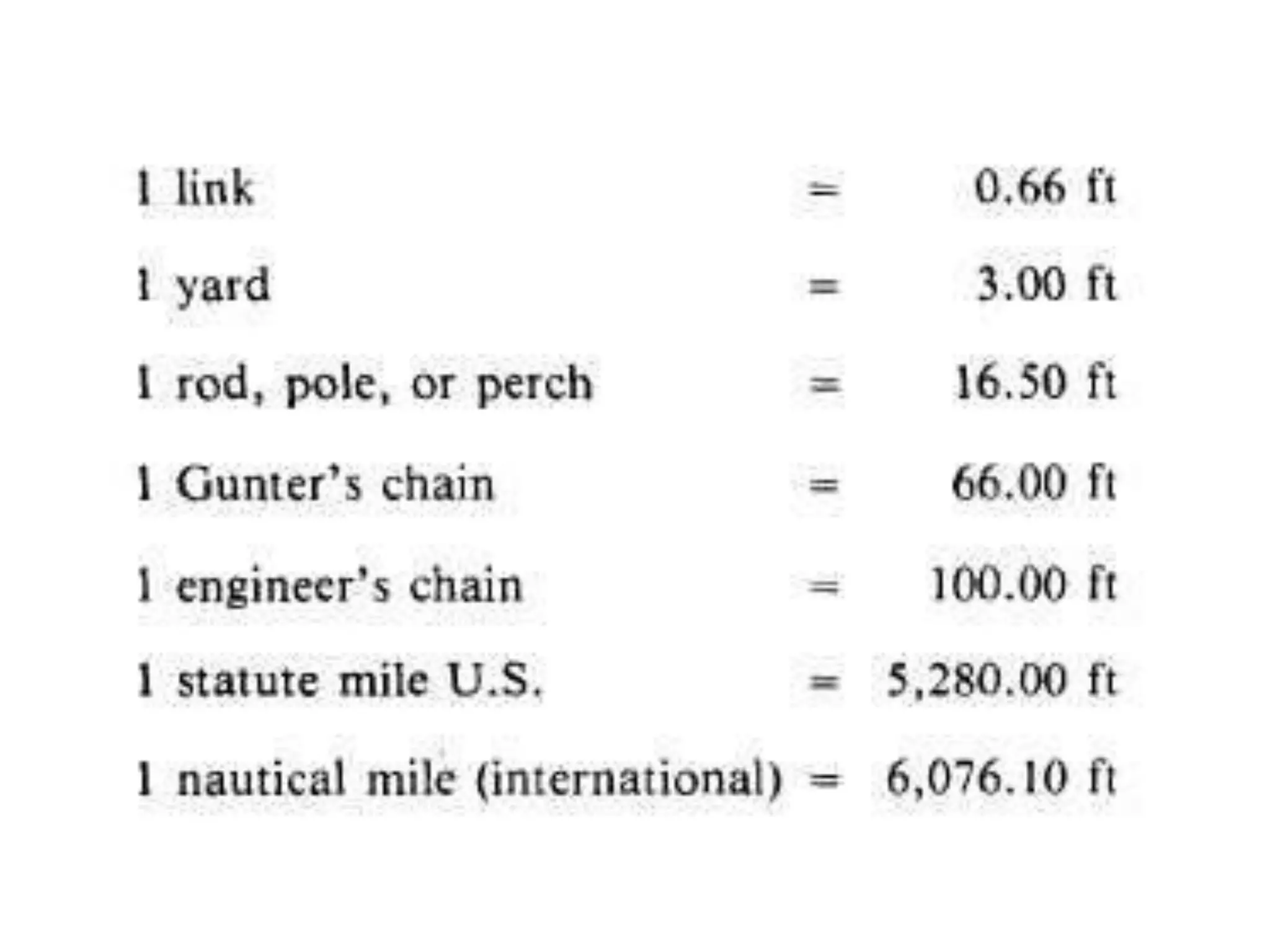
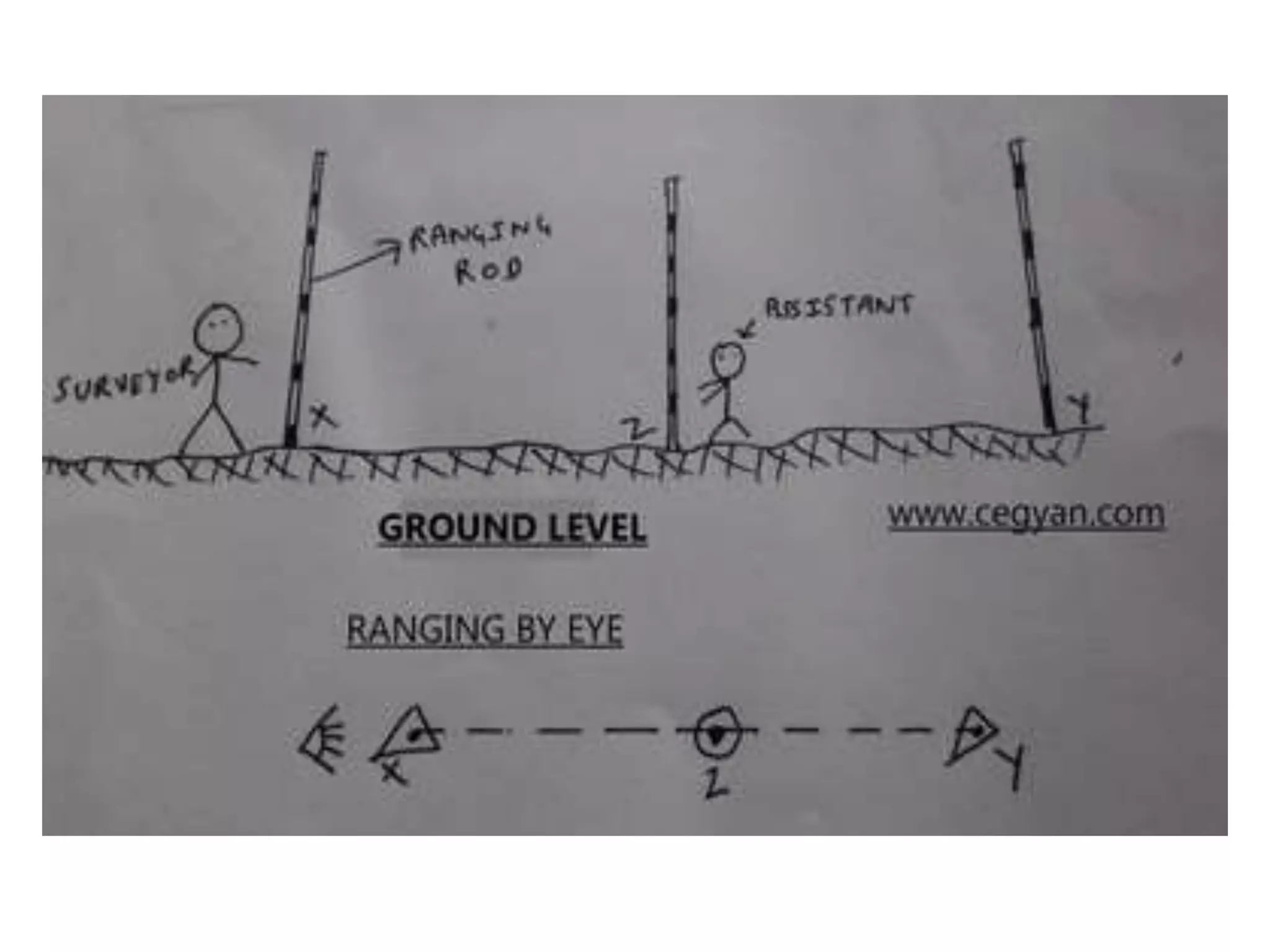
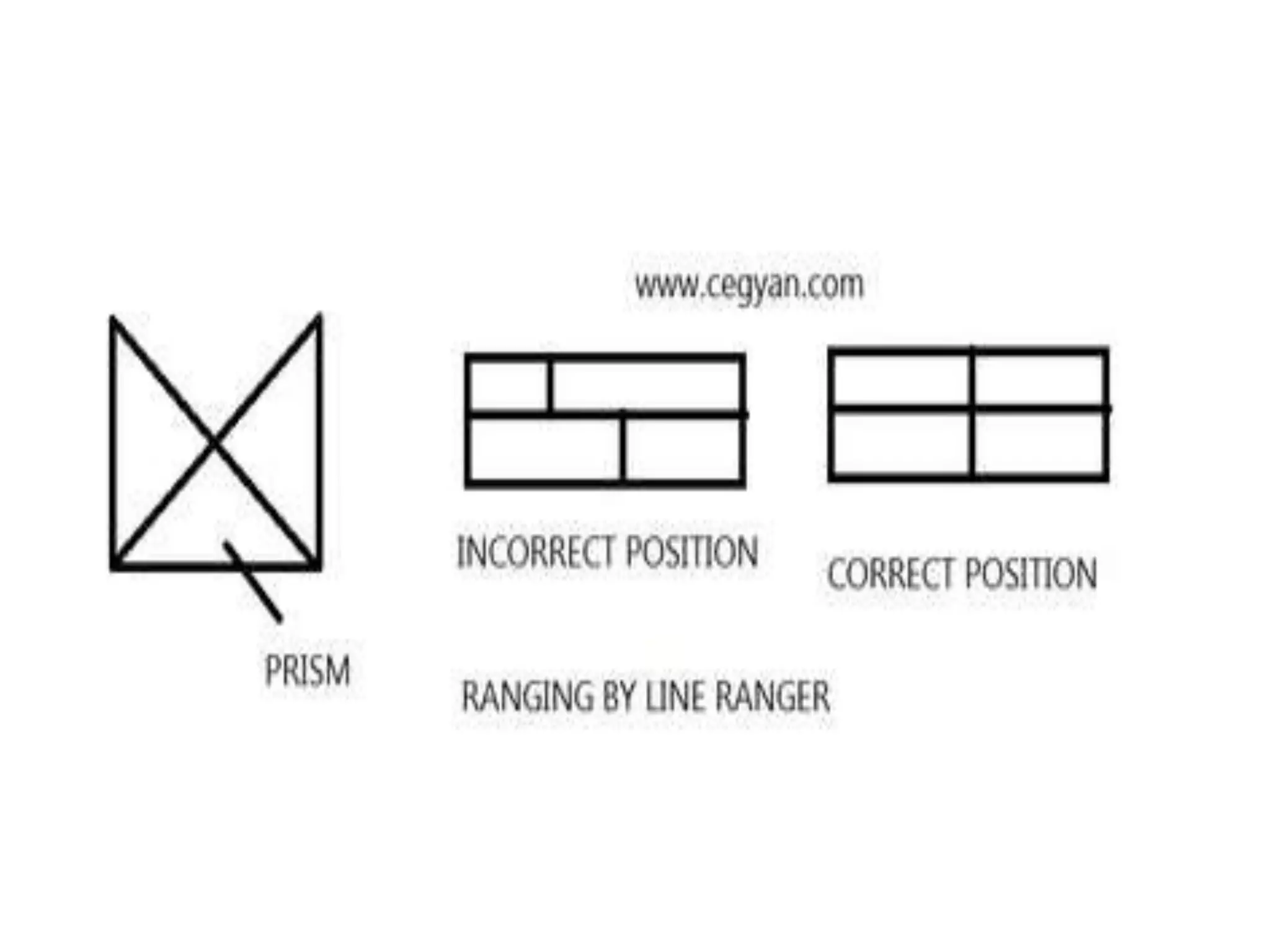
This document discusses various methods of linear measurement used in surveying. It describes chain and tape measurements, including different types of chains, steel bands, and tapes. It also discusses direct and indirect methods of ranging out survey lines when stations are visible or not visible to each other. Finally, it summarizes direct and indirect methods of chaining on sloping ground, including stepping, hypotenuse allowance, and applying slope corrections.

1. DEPARTMENT OF CIVIL
ENGINEERING
Linear Measurement
Methods of Linear Measurements
RANGING OUT SURVEY LINES
Chaining on Sloping Ground
Er. RAMPRASAD KUMAWAT
(M.Tech)

2. Linear Measurement
• Linear measure is defined as a measurement of length. An
example of linear measure is using a yard stick to find out
the length of a table.
• A unit of measurement is simply an arbitrary
length, area, or volume, generally adopted and agreed
upon as a standard unit of measurement's
he basic standard for linear measurement, for
example, is the meter, and the actual length of a meter
is, in the last analysis, equal to the length of a bar of metal
called the International Meter Bar, one replica of which is
kept in the National
Bureau of Standards, Washington, D.C.

4. Methods of Linear Measurements
• Various methods used for linear measurements
may be grouped as:
(i) Approximate
(ii) Using chain or tape
(iii) By optical means and
(iv) Using electromagnetic distance
measurement instruments.

5. Measurement with Chains or Tapes
• Measurement of distances using chain or tape
is termed as chaining. This is the accurate and
commonly employed method in surveying:
These instruments can be classified as
• (i) chain (ii) steel band and (iii) tapes.

6. • (i) Chains: The chains are composed of 100
pieces of 4 mm diameter galvanized mild steel
wires bent into rings at the end and joined to each
other by three circular or oval shaped rings. These
rings give flexibility to the chain. The ends of
chains are provided with swivel joints so that the
chain can be turned without twisting. To facilitate
easy reading of the chain, brass tallies are
provided. End of 10th link from each end is
provided with a Talley of one tooth, 20th link is
provided with a Talley of two teeth; 30th link with
a Talley of three teeth; 40th link with a Talley of 4
teeth and the middle of chain is provided with a
Talley of circular shape.

7. • It is to be noted that
(i) length of a link is the distance between centers of two
consecutive middle rings.
(ii) the length of the chain is from outside of one handle to
the outside of the other handle.
Commonly used metric chains are of 20 m length. They
have 100 links with talleys at every 2 m.
Each link is of 0.2 m length. Simple rings are provided at
every one meter length except wherever tallies are provided.
The total length of chain is marked on the brass handle.
However 30 m chains are also in use. Length of each link is
0.3 m. It is not so convenient as 20 m chain to read, since no
rings can be provided at one meter distance and each link
needs multiplication with 0.3 to arrive at meter units.
However as a result the influence of using 100 ft chain in
olden days, this type of chain are also in market.

8. • Steel Band: It is also known as band chain. It
consists of steel of 12 to 16 mm width and 0.3 to
0.6 mm thickness. The steel ribbon is wound
around an open steel cross or in a metal reel.
Metric steel bands are available in lengths of 20
m and 30 m. Any one of the following two
methods of markings are used:
(i) Providing brass studs at every 0.2 m and
numbering at every meter. Last links from either
end are subdivided in cm and mm.
(ii) Etching graduations as meters, decimeters and
centimeters on one side of the band and 0.2 m
links on the other side.

9. • Tapes: Depending upon the materials used,
they are classified as:
(i) Cloth or Linen Tape.
(ii) Metallic Tape.
(iii) Steel Tape.
(iv) Invar Tape.

10. • (i) Cloth or Linen Tape: 12 to 15 mm wide
cloth or linen is varnished and graduations are
marked. They are provided with brass handle
at the ends. They are available in length of 10
m, 20 m, 25 m and 30 m. These tapes are light
and flexible. However because of the
following disadvantages they are not popular:
• (i) Due to moisture they shrink.
(ii) Due to stretching they extend.
(iii) They are not strong.
(iv) They are likely to twist.

12. • (ii) Metallic Tape: They are made up of
varnished strip of waterproof linen interwoven
with small wires of brass, copper or bronze. End
100 mm length of tapes are provided with leather
or suitable strong plastic materials. Tapes of
length 10 m, 20 m, 30 m and 50 m are available in
a case of leather or corrosion resistant metal fitted
with a winding device. Red and black coloured
markings are used for indicating full meters and
its fractions in centimeters. These tapes are light,
flexible and not easily broken. These tapes are
commonly used in surveying.

14. • (iii) Steel Tape: A steel tape consists of 6 to 10
mm wide strip with metal ring at free end and
wound in a leather or corrosion resistant metal
case. It is provided with a suitable winding
device. Tapes are marked indicating 5 mm,
centimeters, decimeters and meters. The end 10
cm length is marked with millimeters also. 10 m,
20 m, 30 m, or 50 m tapes are used in surveying.
Figure 12.3 shows a typical steel tape (Ref. Plate
12.1 also). Steel tapes are superior to metallic
tapes as far as accuracy is concerned.
However they are delicate. Care should be taken
to wipe clean before winding. They should be
oiled regularly to prevent corrosion.

16. • (iv) Invar Tape: Invar is an alloy of nickel
(36%) and steel. It’s coefficient of thermal
expansion
is low. Hence errors due to variation in
temperature do not affect measurements much.
The width of tape is 6 mm. It is available in
length 30 m, 50 m and 100 m. It is accurate but
expensive.

18. RANGING OUT SURVEY LINES
• Method of locating or establishing
intermediate points on a straight line
between two fixed point or two survey stations
is called as ranging.

19. There are two methods of ranging
1. Direct Method (Two ends of survey line or
stations are inter-visible)
2. Indirect Method (Two ends of survey line or
stations are not inter-visible)

20. • DIRECT METHOD: This method is used
when two ends of survey stations or survey
lines are inter-visible.
•
Direct ranging can be done by 2 methods:
1 ) RANGING BY EYE
2)RANGING BY LINE RANGER

21. 1) RANGING BY EYE
• Consider two pints X and Y which are inter-visible to
each other.
• In this method ranging rod is fixed at station X and Y.
Suppose if we want to locate a point Z on ground which
is in line with XY.
• The surveyor stands half a meter back side of ranging
rod at X in line with XY.
• Assistant then moves another ranging rod under the
guidance of surveyor in such a way that ranging rod
hold by assistant is in the line XY at point Z between X
AND Y.
• Similarly other points can be located by similar way.
Surveyor has to guide assistant by using some hand
signals so that ranging rod comes in the line.

23. 2)RANGING BY LINE RANGER
• Line ranger is a light and easy to use instrument which can
be used for ranging.
• It consists of 2 plane mirrors or 2 right-angled isosceles
prism places one above the another. Diagonals of two prism
are silvered so as to reflect light. Lower prism is fixed while
the upper prism is moveable. Instrument is provided with
handle at bottom which gives ease to the user for using the
instrument.
Two ranging rods are fixed at inter-visible points. Then
surveyor moves with the line ranger. The point where two
images coincide in line ranger is the point in line with two
fixed ranging rods. At this point a pebble is dropped from
the handle of line ranger and point is traced on ground.

25. • INDIRECT RANGING: This method is used
when two ends of survey stations or survey
line are not inter-visible.
• Let X and Y be the 2 stations which are not
inter-visible. So to proceed in straight line
between X and Y process of indirect ranging is
applied.

26. • Two intermediate points M1 and M2
are located in such a way that person standing
with ranging rod at M2 can see M1 and X
whereas person with ranging rod at M1 can see
M2 and Y.
• Now person at M2 will guide the person at M1 to
come in line with M2 and X on a new position
M3. Now the person at M3 will guide the person
at M2 to come to a new position M4 such that
M3, M4 and Y are on same line. Ranging rod is
fixed at M3 & M4 and chaining is continued
along the hill.

28. Chaining on Sloping Ground:
Direct and Indirect Methods |
Surveying
• In surveying, for the purpose of plotting, only
horizontal distances are required. If the ground
is sloping, the horizontal distances are
obtained either directly or indirectly. If the
slope of the country is upto 3°, it is generally
taken as level ground.

29. The direct and indirect methods of finding
horizontal distances on sloping ground
• 1. Direct Method (Stepping Method):
• The method consists in measuring the line in
short horizontal lengths called steps. Suppose
it is required to measure the horizontal
distance between the points A and B. For
convenience and to obtain better results,
chaining is done from top of hill to the toe i.e.
downhill.

30. • The follower holds the zero end of the chain at A
on the ground and the leader with the other handle
of the chain and a ranging rod moves in the
forward direction at a convenient distance apart.
• The leader then stops and the follower directs him
to be in line with B. The leader then stretches the
chain in the horizontal position and transfers the
end point of the chain on the ground with the help
of a plumb-bob or ordinarily with a ranging rod or
by dropping a piece of stone.

31. • The follower then moves and reaches the
station occupied by the leader and then the
leader moves in the forward direction. The
process is repeated for several times until the
whole line is chained. The lengths of all the
steps are added up so as to obtain the total
horizontal distance. In this case, the horizontal
distance between AB = Ap + Pq + Qr + Rb.

32. • Note:
• The vertical distance between the end of the chain
and the point vertically below it on the ground
such as pP, qQ etc. should not exceed 1.8 m
(man’s height) as otherwise the chain cannot be
stretched to the horizontal position i.e. a sag
would occur in the chain and the measured length
will be more than the actual length of the step.
Therefore when the slope of the ground is steep,
the chain of smaller length is used. For this
purpose, the chain may be broken into different
portions say 10, 20, 30 or 50 links.

33. • 2. Indirect Method:
• The whole length of the line is first of all
divided into different sections having
approximately the same slope. Horizontal
distance is calculated for each section
separately and the total horizontal distance is
then obtained by summing up all the horizontal
distances of different sections.

34. The horizontal distance for each section may
be found out by any of the following indirect
methods:
• (i) The distance along the slope is measured
and then the angle of slope i.e. angle between
the sloping ground and the horizontal surface
is found with the help of Abney’s level or
precisely with theodolite. Knowing the sloping
distance say I and angle of slope say α
horizontal distance, D can be calculated by the
relation, D = I cos α

35. • (ii) The distance along the slope is measured
with chain and the difference in elevation
between the first and the end stations is found
with the help of any levelling instrument

36. The correction may be calculated
• Let α = the angle of slope of the ground.
• AD = AB = 1 Chain = 100 links.
• Then AC = 100 sec α links and BC = AC – AB
= 100 (Sec α- 1) links.
• The amount 100 (sec α – 1) is known as
hypotenusal allowance.

37. • The chain is stretched in the direction AB and
the arrow is placed in advance of the end B of
the chain by an amount equal to (BC), the
hypotenusal allowance, such that the
horizontal equivalent of the total distance i.e.
(chain length + hypotenusal allowance)is equal
to one chain length. The next chain length
starts from C. The process is continued until
the end of the line is reached. The required
horizontal distance is the equal to number of
chains measured.

38. Comparison between direct and indirect
methods of chaining on sloping ground:
• Direct or Stepping Method:
• It is more convenient and rapid if the slopes
are short, steep and of varying degree. The
distances measured are sufficiently correct if
the end points of the chain are transferred
correctly on to the ground and the sag in the
chain due to weight of the chain and
insufficient pull is avoided.

39. • Indirect Method:
• It is more accurate and rapid when the slopes
are long, regular and gentle. The third indirect
method in which the correction for
hypotenusal allowance is applied to each chain
length is usually employed in route surveys.

40. Correction for Slope:
• Horizontal distances can also be determined by
applying negative corrections to the distance
measured along the slope.
• The formulae may be derived as follows:
• (i) Correction for slope if the vertical
distance between first and the last points is
known:

41. • I = the slope distance AB
• h = the vertical distance BB1 between two
points A and B
• D = the horizontal distance AB1
• Ch= the correction to the
• The correction is to be subtracted from the
slope distance in order to obtain its horizontal
equivalent.

42. (ii) Correction for slope if the angle
of slope is known:
• If the angle of slope of the ground is measured
with greater precision such as with a
theodolite, then the correction for slope should
be determined by the following exact formula.

43. • THANKS!
Gmail:-
ramkumawat001@gmail.com