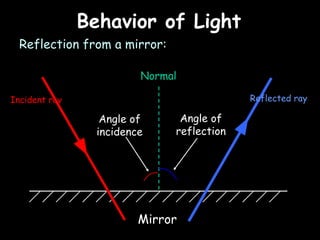
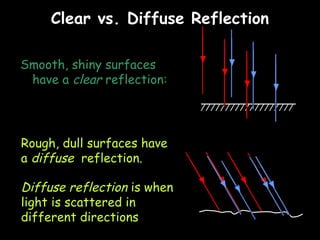
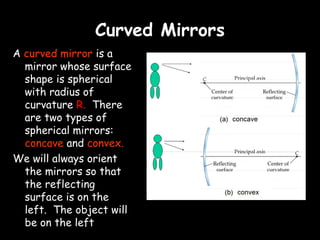
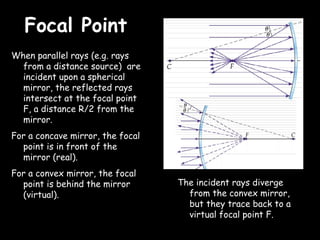
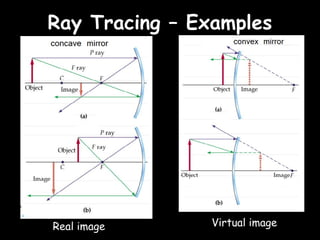
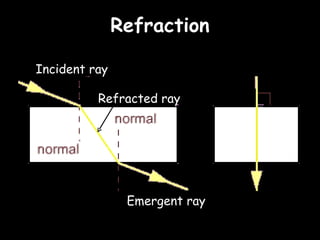
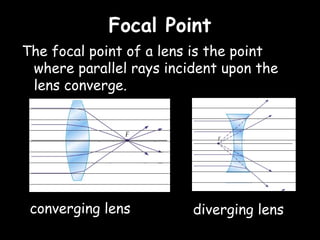
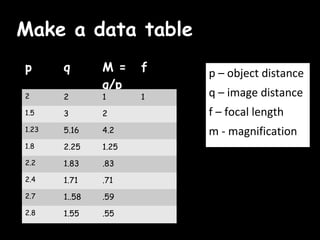
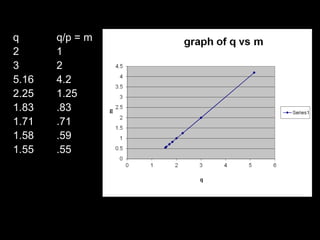
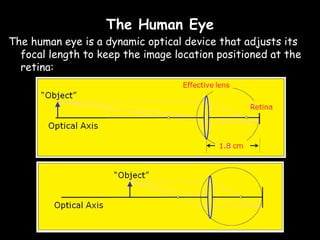
The eye accommodates by increasing its lens power to 59.6 diopters. 2. The lens power is 59.6 diopters & the focal length is: f = 0.25 m 3. The near point for a normal eye is 0.25 m. 4. Presbyopia occurs when the eye loses its ability to accommodate for close objects. The near point increases beyond 0.25 m. So in summary, the eye changes its focal length to focus on objects at different distances by changing its lens power through accommodation.

1. Focus questions
What is the wave nature of light?
How does light behave?
What are the primary colors of
light? of pigments?
How are images formed?

2. Light and Sight

3. Light And Sight
Properties of light
Behavior of light
Reflection
Formation of images in mirrors
Refraction
Color
Formation of images in lenses
The Human Eye

4. Light a form of energy

5. Part 1 – Properties of Light
Light travels in straight lines:
Laser

6. Light travels VERY FAST – around
300,000 kilometres per second.
At this speed it can
go around the world 8
times in one second.

7. Light travels much faster than sound. For example:
1) Thunder and lightning
start at the same time,
but we will see the
lightning first.
2) When a starting pistol
is fired we see the
smoke first and then
hear the bang.

8. We see things because they
reflect light into our eyes:
Homework

9. Luminous and non-luminous objects
A luminous object is one that produces light.
A non-luminous object is one that reflects light.
Luminous objects Reflectors

10. Shadows
Shadows are places where light is “blocked”:
Rays of light

11. Properties of Light summary
1) Light travels in straight lines
2) Light travels much faster than sound
3) We see things because they reflect light
into our eyes
4) Shadows are formed when light is blocked
by an object

12. Behavior of Light:Reflection

13. Behavior of Light
Reflection from a mirror:
Normal
Incident ray Reflected ray
Angle of Angle of
incidence reflection
Mirror

14. The Law of Reflection
Angle of incidence = Angle of reflection
In other words, light gets reflected from a surface at
____ _____ angle it hits it.
The
same !!!

15. Clear vs. Diffuse Reflection
Smooth, shiny surfaces
have a clear reflection:
Rough, dull surfaces have
a diffuse reflection.
Diffuse reflection is when
light is scattered in
different directions

16. Behavior of Light
Image formation in mirrors

17. The Law of Reflection
For specular reflection the incident angle θi
equals the reflected angle θr:
θi = θr
The angles are
measured
relative to the
normal, shown
here as a
dotted line.

18. Image formed by a Plane Mirror
A mirror is an object that reflects light. A
plane mirror is simply a flat mirror.
Consider an object placed at point P in front of
a plane mirror. An image will be formed at
point P´ behind the mirror.
do = distance from object to mirror
di = distance from image to mirror
ho = height of object
hi = height of image
For a plane mirror: hi
do = -di and ho = hi
Image is behind mirror: di < 0

19. Images
An image is formed at the point where the rays
of light leaving a single point on an object
either actually intersect or where they appear
to originate from.
If the light rays actually do intersect, then the
image is a real image. If the light only appears
to be coming from a point, but is not physically
there, then the image is a virtual image.
We define the magnification, m, of an image to
be: image height hi di
m= = =−
object height ho do
If m is negative, the image is inverted (upside
down).

20. Plane Mirrors
A plane mirror image has the following
properties:
The image distance equals the object distance ( in
magnitude )
The image is unmagnified
image height hi d
m= = =− i
object height ho do
The image is virtual: do di
 negative image distance
 di < 0
m>0, The image is not inverted

21. Curved or Spherical mirrors

22. Curved Mirrors
A curved mirror is a
mirror whose surface
shape is spherical
with radius of
curvature R. There
are two types of
spherical mirrors:
concave and convex.
We will always orient
the mirrors so that
the reflecting
surface is on the
left. The object will
be on the left.

23. Focal Point
When parallel rays (e.g. rays
from a distance source) are
incident upon a spherical
mirror, the reflected rays
intersect at the focal point
F, a distance R/2 from the
mirror.
For a concave mirror, the focal
point is in front of the
mirror (real).
For a convex mirror, the focal
point is behind the mirror The incident rays diverge
(virtual). from the convex mirror,
but they trace back to a
virtual focal point F.

24. Focal Length
The focal length f is the
distance from the surface
of the mirror to the focal
point.
CF = FA = radius = FM
The focal length FM is half the radius of curvature of a
spherical mirror.
Sign Convention: the focal length is negative if the
focal point is behind the mirror.
For a concave mirror, f = ½R
For a convex mirror, f = −½R (R is always positive)

25. Ray
Tracing
It is sufficient to
use two of four
principal rays to
determine where
an image will be
located.
The parallel ray (P ray) reflects
through the focal point. The
focal ray (F ray) reflects parallel
to the axis, and the center-of-
curvature ray (C ray) reflects
back along its incoming path.
The Mid ray (M ray) reflects
with equal angles at the axis of
symmetry of the mirror.

26. Ray Tracing – Examples
Real image Virtual image

27. The Mirror Equation
The ray tracing technique Sign Conventions:
shows qualitatively where
the image will be located. do is positive if the object is in
The distance from the front of the mirror (real object)
mirror to the image, di, do is negative if the object is in
can be found from the back of the mirror (virtual
mirror equation: object)
1 1 1 di is positive if the image is in front
+ =
do di f of the mirror (real image)
do = distance from object to di is negative if the image is behind
mirror the mirror (virtual image)
di = distance from image to f is positive for concave mirrors
mirror f is negative for convex mirrors
di
f = focal length m = − d m is positive for upright images
o

28. Using mirrors
Two examples:
2) A car headlight
1) A periscope

29. How do you explain these?

30. Refraction
Incident ray
Refracted ray
Emergent ray

31. Refraction

32. Refraction

33. The Refraction of Light
The speed of light is
different in different materials. We define the index of
refraction, n, of a material to be the ratio of the speed of light in
vacuum to the speed of light in the material:
n = c/v
When light travels from
one medium to another its velocity and wavelength change, but its
frequency remains constant.

34. Snell’s Law
In general, when light enters a new material its direction
will change. The angle of refraction θ2 is related to the
angle of incidence θ1 by Snell’s Law:
sin θ1 sin θ2
= = constant
v1 v2
where v is the velocity of light in the medium.
Snell’s Law can also be written as
n1sinθ1 = n2sinθ2
The angles θ1 and θ2 are
measured relative to the
line normal to the surface
between the two materials.

35. Colour
White light is not a single colour; it is made
up of a mixture of the seven colours of the
rainbow.
We can demonstrate this by
splitting white light with a
prism:
This is how rainbows are
formed: sunlight is “split up”
by raindrops.

36. The colours of the rainbow:
Red
Orange
Yellow
Green
Blue
Indigo
Violet

37. Why are objects colored?

38. Adding colours
White light can be split up to make separate colours.
These colours can be added together again.
The primary colours of light are red, blue and green:
Adding blue and red Adding blue and
makes magenta green makes cyan
(purple) (light blue)
Adding red Adding all
and green three makes
makes yellow white again

39. Seeing colour
The colour an object appears depends on the colours
of light it reflects.
For example, a red book only reflects red light:
White Only red light
light is reflected

40. A pair of purple trousers would reflect purple light
(and red and blue, as purple is made up of red and blue):
Purple light
A white hat would reflect all seven colours:
White
light

41. Using coloured light
If we look at a coloured object in coloured
light we see something different. For
example, consider a this pair of shirt and
shorts:
Shirt looks red
White
light
Shorts look blue

42. In different colours of light they would look different:
Red
Shirt looks red
light
Shorts look black
Shirt looks black
Blue
light
Shorts look blue

43. Some further examples:
Colour object
Object Colour of light
seems to be
Red Red
Red socks Blue Black
Green Black
Red Black
Blue teddy Blue
Green
Red
Green camel Blue
Green
Red
Magenta book Blue
Green

44. Using filters
Filters can be used to “block” out different colours of light:
Red
Filter
Magenta
Filter

45. Investigating filters
Colour of filter Colours that could be “seen”
Red
Green
Blue
Cyan
Magenta
Yellow

46. Red Blue Green White
Yellow Cyan Magenta

47. Lenses
Light is reflected from a
mirror. Light is
refracted through a
lens.

49. Focal Point
The focal point of a lens is the point
where parallel rays incident upon the
lens converge.
converging lens diverging lens

50. How does a lens form an image?

51. Ray Tracing for Lenses
Just as for
mirrors we use
three “easy” rays
to find the image
from a lens. The
lens is assumed to
be thin.
The P ray propagates parallel to the principal axis until it
encounters the lens, where it is refracted to pass through the
focal point on the far side of the lens. The F ray passes through
the focal point on the near side of the lens, then leaves the lens
parallel to the principal axis. The M ray passes through the
middle of the lens with no deflection (in thin lens limit).

52. The Lens Equation
http://www.physics.uoguelph.ca/applets/Intro_phy

53. Data and Analysis
How does the image distance q of a convex
lens change as the object distance p is
decreased?
How does the height of the image change as
the object distance is decreased?
Write the equation in determining the linear
magnification m of a convex lens using p
and q. Call this Eq (1)

54. Data and Analysis
Using Excel graph m vs q. What does the graph
show?. When m is zero, what is q?. This is the q
intercept. Relate this observation with your
answer to (c). Compare the value of the q
intercept with the focal length of the mirror.
What then is the physical meaning of the q-
intercept?
Extend your graph until it intersects the vertical
axis m. Compute the slope of your graph. Compare
the value of the slope and the q-intercept. How
are they related?. Express the relationship IN AN
EQAUTION using the physical meaning of the q –
intercept you found. Call this Eq (2).
Write the equation of the line graph. Call this Eq (3)

55. Make a data table
p q M = f p – object distance
q/p
2 2 1 1 q – image distance
1.5 3 2 f – focal length
1.23 5.16 4.2 m - magnification
1.8 2.25 1.25
2.2 1.83 .83
2.4 1.71 .71
2.7 1..58 .59
2.8 1.55 .55

56. q q/p = m
2 1
3 2
5.16 4.2
2.25 1.25
1.83 .83
1.71 .71
1.58 .59
1.55 .55

57. The Thin Lens Equation
The ray tracing technique shows 1 1 1
qualitatively where the image from a lens
will be located. The distance from the
1+ 1 = 1
do + di = f
lens to the image, can be found from the do di f
thin-lens equation:
Sign Conventions:
do is positive for real objects (from which light diverges)
do is negative for virtual objects (toward which light
converges)
di is positive for real images (on the opposite side of the
lens from the object)
di is negative for virtual images (same side as object)
f is positive for converging (convex) lenses
f is negative for diverging (concave) lenses
m is positive for upright images

58. The eye and the camera

59. The eye model

60. The Human Eye
The human eye is a dynamic optical device that adjusts its
focal length to keep the image location positioned at the
retina:

61. Optics of the Eye
1. The “normal” eye can be modeled as a simple lens system
with an effective focal length (& optical power) and a
fixed image distance, i:
1 1 1
= +
f p 0.018m
2. The job of the eye is to focus images on the retina. The
image distance is therefore fixed at 1.8 cm (or 0.018 m).
3. When the eye cannot adequately focus an image on the
retina, correction may be needed
4. The 4 common vision problems:
a. Myopia (near sightedness, short far & near point)
b. Hypermetropia (far sightedness, long far & near point)
c. Astigmatism (warped lens optics, focal length not uniform on all
axes in the eye)
d. Presbyopia (normal distance vision but inability to accommodate
for close objects)

62. Distance Vision Optics
1. When viewing distant objects, the lens power of
the eye (& focal length) of the eye is given by:
1 1 1 1
= + = = 55.6 m-1
f ∞ 0.018 m 0.018 m
2. The lens power is 55.6 diopters & the focal
length is:
f = 0.018 m
1. When a person is near sighted (myopic), he/she
cannot see objects at infinity (“infinity” is the
“far point” for a normal eye)
– Myopic far point < Normal far point

63. Distance Vision Optics
Example: A person with -2.0 diopter
distance correction.
a. This person has a lens power of 57.6 & needs
this “minus” correction to lower the effective
lens power to a “normal” 55.6:
1 1 1
= + = 57.6 diopters ⇒ p = 2.0 m
f p 0.018 m
b. The far point for this person is: p = 2 m {any
object beyond this distance is not in focus}

64. Near Vision Optics
1. When viewing close-in objects, the lens power of
the eye (& focal length) of the eye is given by:
1 1 1
= + = 59.6 m-1
f 0.25 m 0.018 m
2. The lens power is 59.6 diopters & the focal
length is: f = 0.0168 m
3. A far sighted (hyperopic) person cannot see
objects at close distances even though the eye is
accomodating normally
– Hyperopic near point > Normal near point (0.25 m)

65. Near Vision Optics
Example: A person with +2.0 diopter vision correction.
a. This person has a (near) lens power of 57.6 & needs
this “plus” correction to raise the effective lens power
to a “normal” close distance power of 59.6:
1 1 1
= + = 57.6 diopters ⇒ p = 0.49 m
f p 0.018 m
b. The near point for this person is: p = 0.49 m {any
object closer is not in focus}
c. People w/presbyopia have normal distance lens power
but are unable to adjust for closer objects, thus
needing “reader” glasses