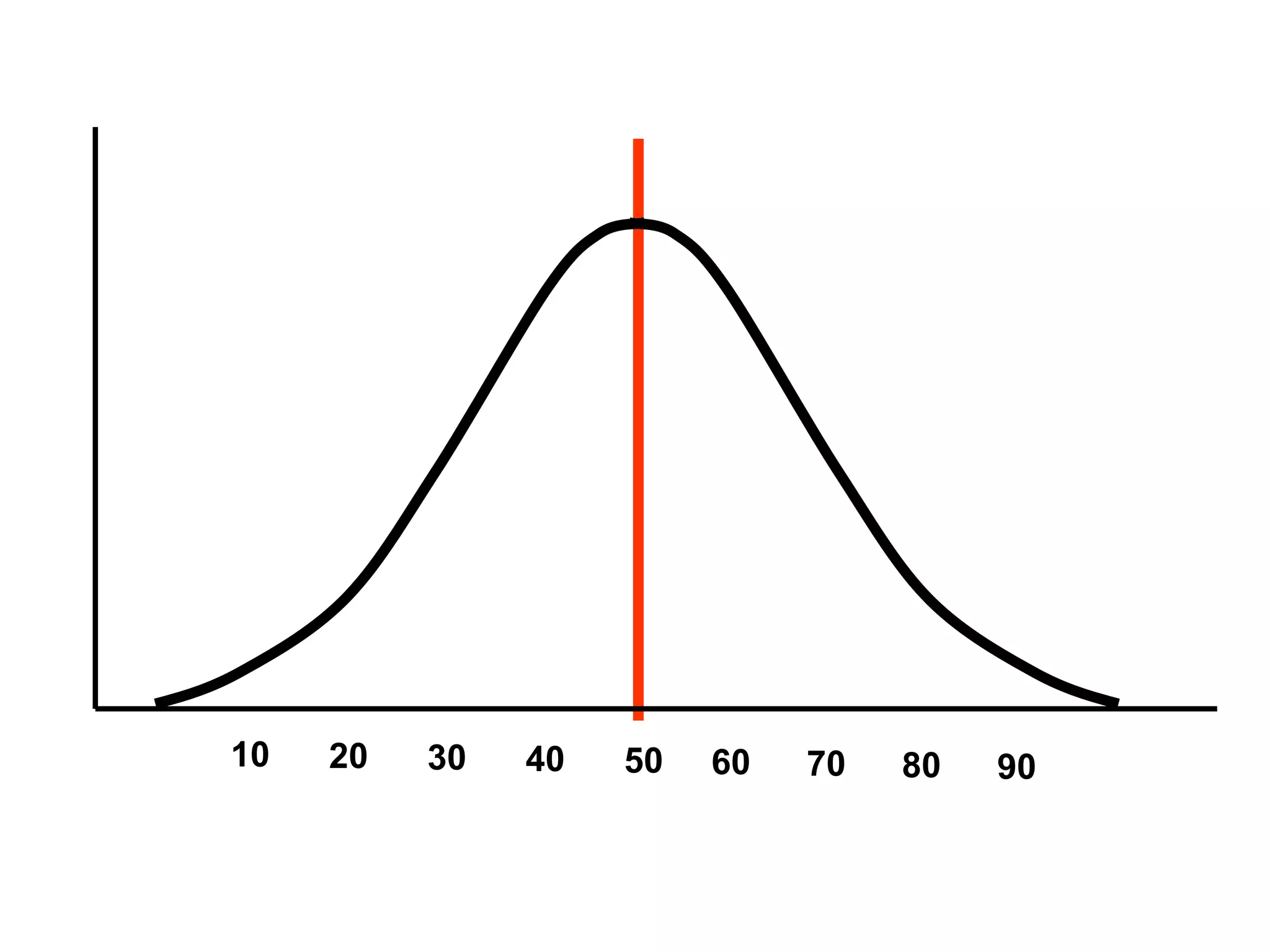
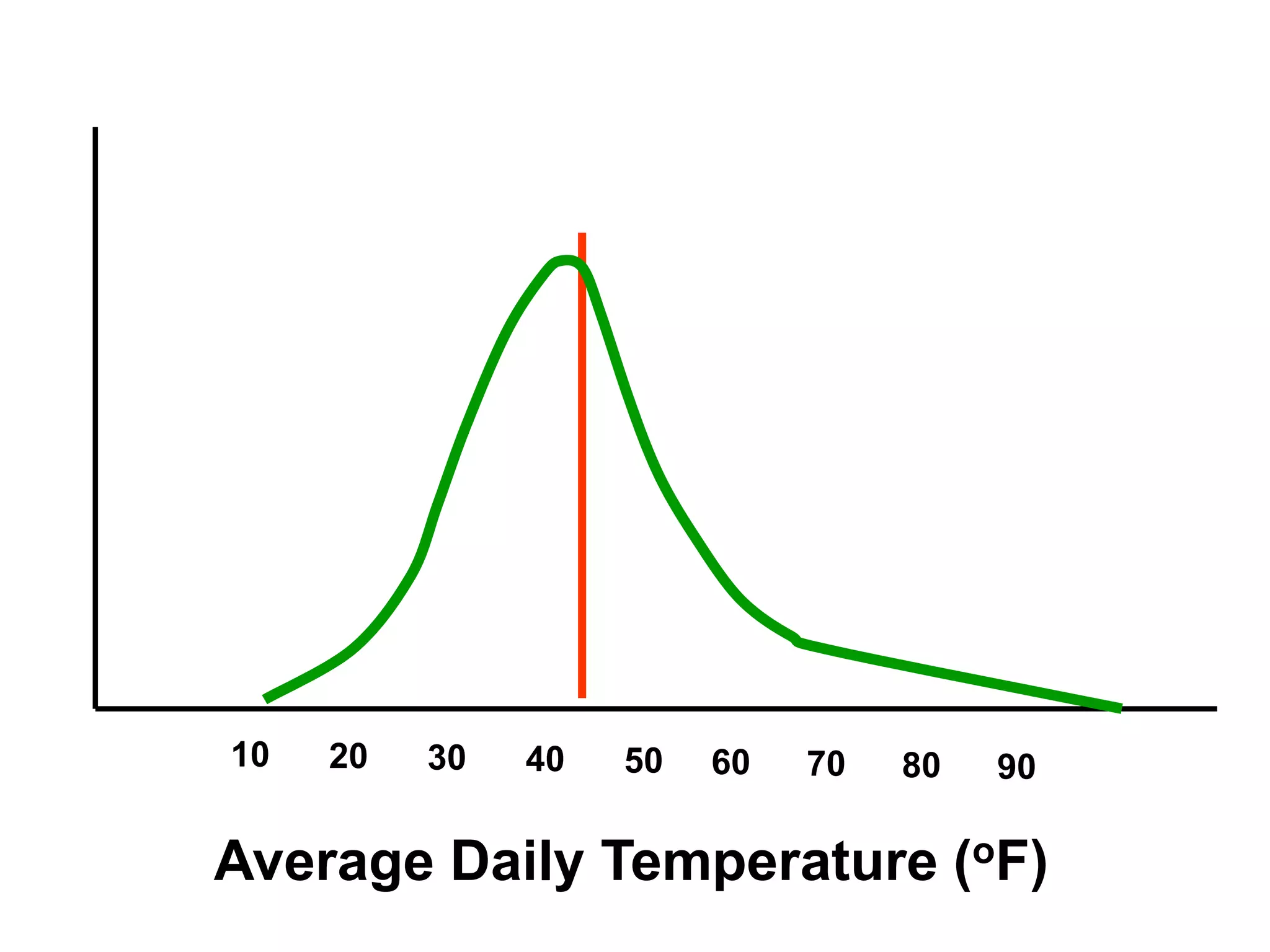
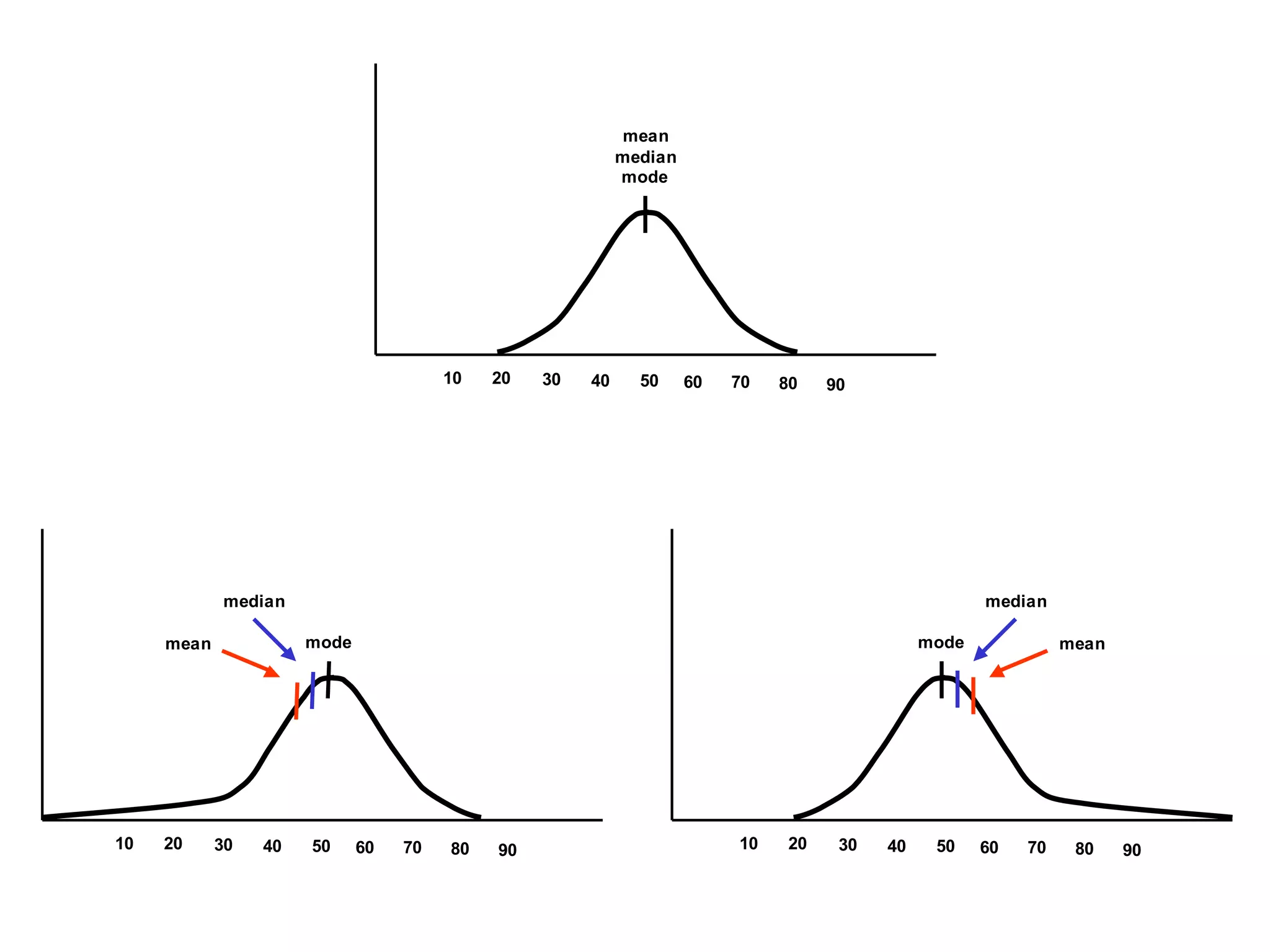
This document discusses measures of central tendency, which convey the most information about distributions. The three main measures are the mode, median, and mean. The mode is the most frequently occurring value. The median is the midpoint value when data are ordered from smallest to largest. The mean is the average value. Which measure is most appropriate depends on the level of measurement and intent of the communication. The mode is suitable for any level, while the median and mean are best for interval/ratio data. These measures may differ depending on the shape of the distribution.

1. Measures of
Central Tendency
Chapter 4
Homework: 1, 2, 3, 5, 6, 13
Ignore parts with eye-ball estimation

2. 3 essential characteristics
of distributions
 Conveys most info for most distributions
1. Where is middle of distribution?
2. How wide is distribution?
3. What is shape of the distribution? ~

3. Central Tendency
 Middle of distribution
 measures: mode, median, mean
 Portable & compact communication
 further simplification of data
 lose more detail
 Which most appropriate?
 Depends on level of measurement
 intent of your communication ~

4. Mode
 Most frequently occurring value
 appropriate for any measurement
level
nominal, ordinal, interval/ratio ~

5. Computing the Mode
 Frequency distribution
 most frequently occurring value
 Grouped frequency distribution
 find interval with highest frequency
 report midpoint
e.g., interval: 150 to 160
report: (160 + 150)/2 = 155
 Methods may produce different
results ~

6. Frequency Distribution
X f
19 1
18 2
16 3
15 3
14 5
13 2
12 6
11 7
10 3
9 6
8 5
7 3
6 2
5 2
50
mode = 11
Computing the Mode
Grouped
Frequency
Distribution
X f
19-20 1
17-18 2
15-16 6
13-14 7
11-12 13
9-10 9
7- 8 8
5- 6 4
50
mode =

7. Grouped
Frequency
Distribution
X f
81-100 1
61-80 3
41-60 4
21-40 9
1-20 2
mode =

8. Median
 Midpoint of a data set
 values ½ smaller, ½ larger
 appropriate for ordinal & interval/ratio
NOT nominal ~

9. 10 20 30 40 50 60 70 80 90

10. 10 20 30 40 50 60 70 80 90
Average Daily Temperature (oF)

11. Finding the Median
1. List all values from largest---> smallest
if f=3, then list 3 times
2. Odd # entries median = middle value
middle = (n + 1)/2
3. Even # entries = half way b/n middle 2
values ~

12. Finding the Median: odd # f
X
9
7
5
3
1
f
2
1
3
3
2
11
9
9
7
5
5
5
3
3
3
1
1
(n + 1)/2 =

13. Finding the Median: even # f
X
9
7
5
3
1
f
2
1
3
3
3
12
9
9
7
5
5
5
3
3
3
1
1
1
n /2 =
(n /2) + 1 =
median =
Average middle 2 values

14. Mean
 Average
 value on X-axis
 may not be actual value in data set
 Computing the mean
Sample mean
n
X
X

Population mean
N
X

15. Reporting Central Tendency
 Depends on level of measurement
 Nominal: mode only appropriate
 Ordinal: mode & median
 not mean ---> uneven intervals
 Interval/ratio: all 3 appropriate ~

16. Comparing the Measures
 Normal distribution
 all 3 coincide
 Skewed will not be same values
 greatest effect of mean
less on median, least on mode
 positive: mode -->median-->mean
 negative: mean <--median<--mode

17. 10 20 30 40 50 60 70 80 90
mode
median
mean
10 20 30 40 50 60 70 80 90
mode
median
mean
10 20 30 40 50 60 70 80 90
mode
median
mean