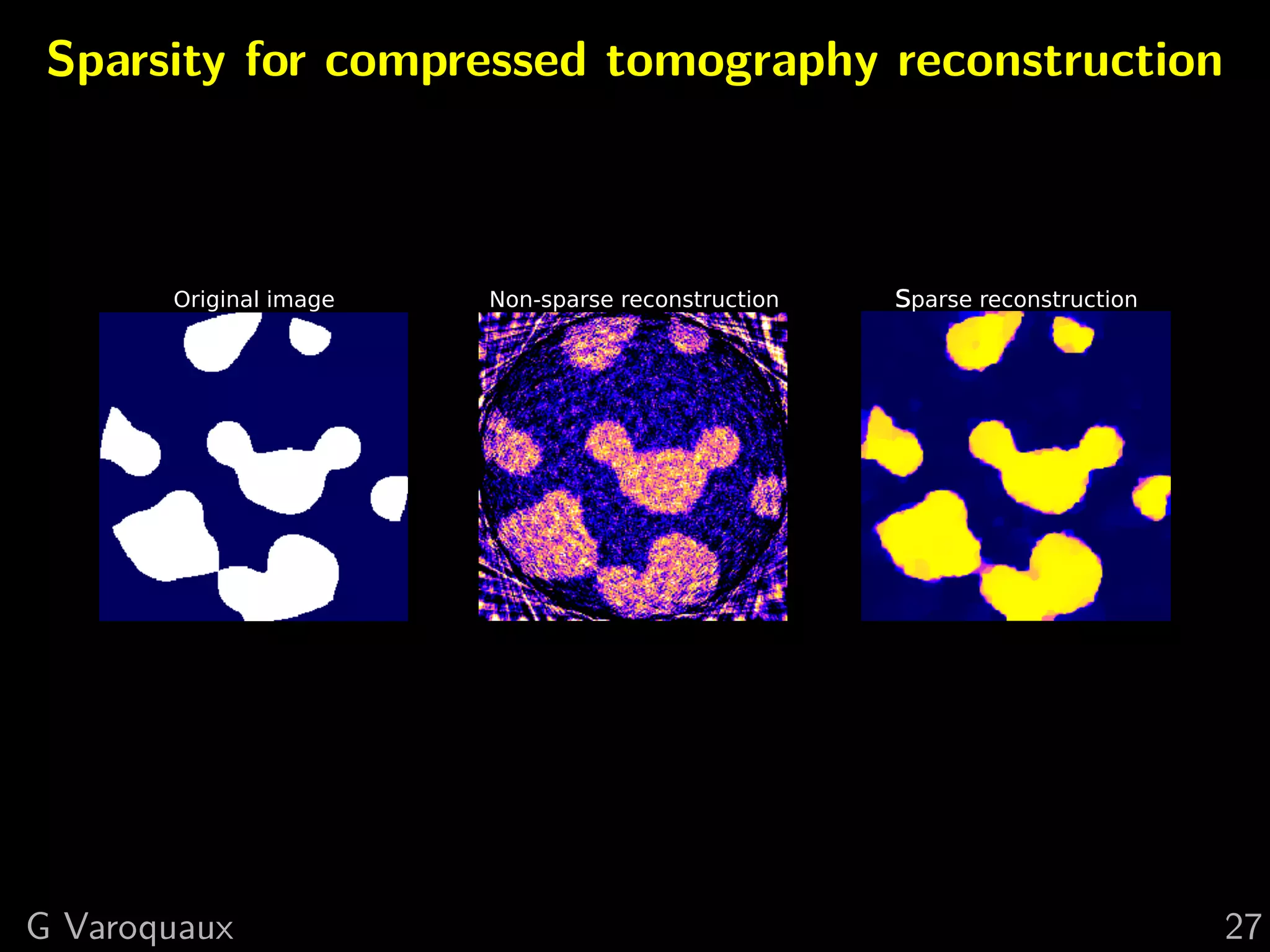
The document provides a hand-waving introduction to using sparsity for compressed tomography reconstruction. It discusses how imposing sparsity can help solve ill-posed inverse problems with limited data by finding sparse solutions. Mathematical formulations are presented using L1-norm minimization and techniques like total variation. Optimization algorithms like iterative shrinkage-thresholding are described, which use proximal operators to handle non-smooth terms in the objective function.

1. A hand-waving introduction to sparsity
for compressed tomography reconstruction
Ga¨l Varoquaux and Emmanuelle Gouillart
e
Dense slides. For future reference: http://www.slideshare.net/GaelVaroquaux

2. 1 Sparsity for inverse problems
2 Mathematical formulation
3 Choice of a sparse representation
4 Optimization algorithms
G Varoquaux 2

3. 1 Sparsity for inverse problems
Problem setting
Intuitions
G Varoquaux 3

4. 1 Tomography reconstruction: a linear problem
y = Ax
0
20
40
60
80
0 50 100 150 200 250
y ∈ Rn, A ∈ Rn×p, x ∈ Rp
n ∝ number of projections
p: number of pixels in reconstructed image
We want to find x knowing A and y
G Varoquaux 4

5. 1 Small n: an ill-posed linear problem
y = Ax admits multiple solutions
The sensing operator A has a large null space:
images that give null projections
In particular it is blind to high spatial frequencies:
G Varoquaux 5

6. 1 Small n: an ill-posed linear problem
y = Ax admits multiple solutions
The sensing operator A has a large null space:
images that give null projections
In particular it is blind to high spatial frequencies:
Large number of projections
Ill-conditioned problem:
“short-sighted” rather than blind,
⇒ captures noise on those components
G Varoquaux 5

7. 1 A toy example: spectral analysis
Recovering the frequency spectrum
Signal Freq. spectrum
signal = A · frequencies
0
2
4
6
8 ...
0 10 20 30 40 50 60
G Varoquaux 6

8. 1 A toy example: spectral analysis
Sub-sampling
Signal Freq. spectrum
signal = A · frequencies
0
2
4
6
8 ...
0 10 20 30 40 50 60
Recovery problem becomes ill-posed
G Varoquaux 6

9. 1 A toy example: spectral analysis
Problem: aliasing
Signal Freq. spectrum
Information in the null-space of A is lost
G Varoquaux 7

10. 1 A toy example: spectral analysis
Problem: aliasing
Signal Freq. spectrum
Solution: incoherent measurements
Signal Freq. spectrum
i.e. careful choice of null-space of A
G Varoquaux 7

11. 1 A toy example: spectral analysis
Incoherent measurements, but scarcity of data
Signal Freq. spectrum
The null-space of A is spread out in frequency
Not much data ⇒ large null-space
= captures “noise”
G Varoquaux 8

12. 1 A toy example: spectral analysis
Incoherent measurements, but scarcity of data
Signal Freq. spectrum
The null-space of A is spread out in frequency
Not much data ⇒ large null-space
Sparse Freq. spectrum
= captures “noise”
Impose sparsity
Find a small number of frequencies
to explain the signal
G Varoquaux 8

13. 1 And for tomography reconstruction?
Original image Non-sparse reconstruction Sparse reconstruction
128 × 128 pixels, 18 projections
http://scikit-learn.org/stable/auto_examples/applications/
plot_tomography_l1_reconstruction.html
G Varoquaux 9

14. 1 Why does it work: a geometric explanation
Two coefficients of x not in the null-space of A:
x2
y=
Ax
xtrue
x1
The sparsest solution is in the blue cross
It corresponds to the true solution (xtrue )
if the slope is > 45◦
G Varoquaux 10

15. 1 Why does it work: a geometric explanation
Two coefficients of x not in the null-space of A:
x2
y=
Ax
xtrue
x1
The sparsest solution is in the blue cross
It corresponds to the true solution (xtrue )
if the slope is > 45◦
The cross can be replaced by its convex hull
G Varoquaux 10

16. 1 Why does it work: a geometric explanation
Two coefficients of x not in the null-space of A:
x2
y=
Ax xtrue
x1
The sparsest solution is in the blue cross
It corresponds to the true solution (xtrue )
if the slope is > 45◦
In high dimension: large acceptable set
G Varoquaux 10

17. Recovery of sparse signal
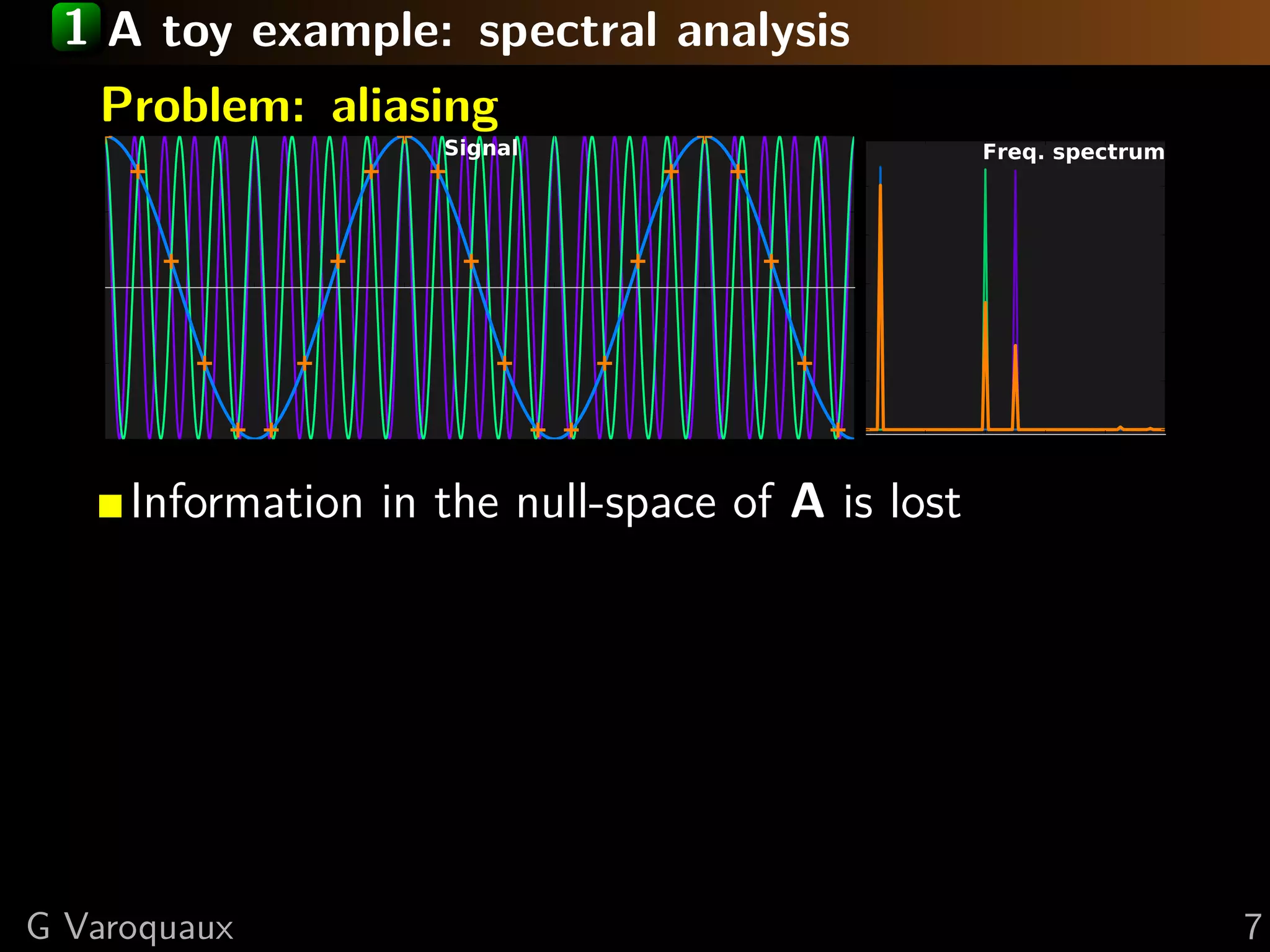
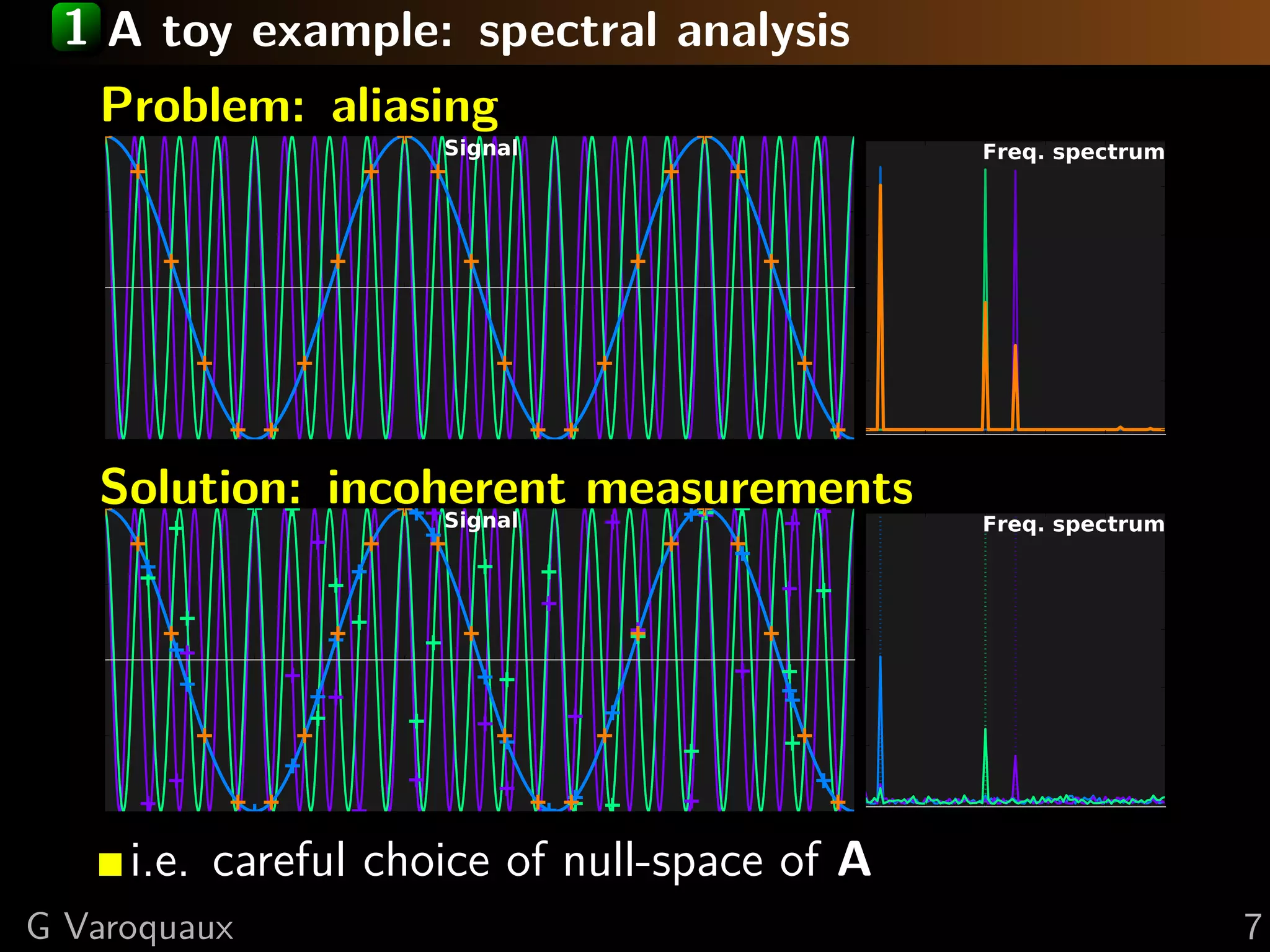
Null space of sensing operator incoherent
with sparse representation
⇒ Excellent sparse recovery with little projections
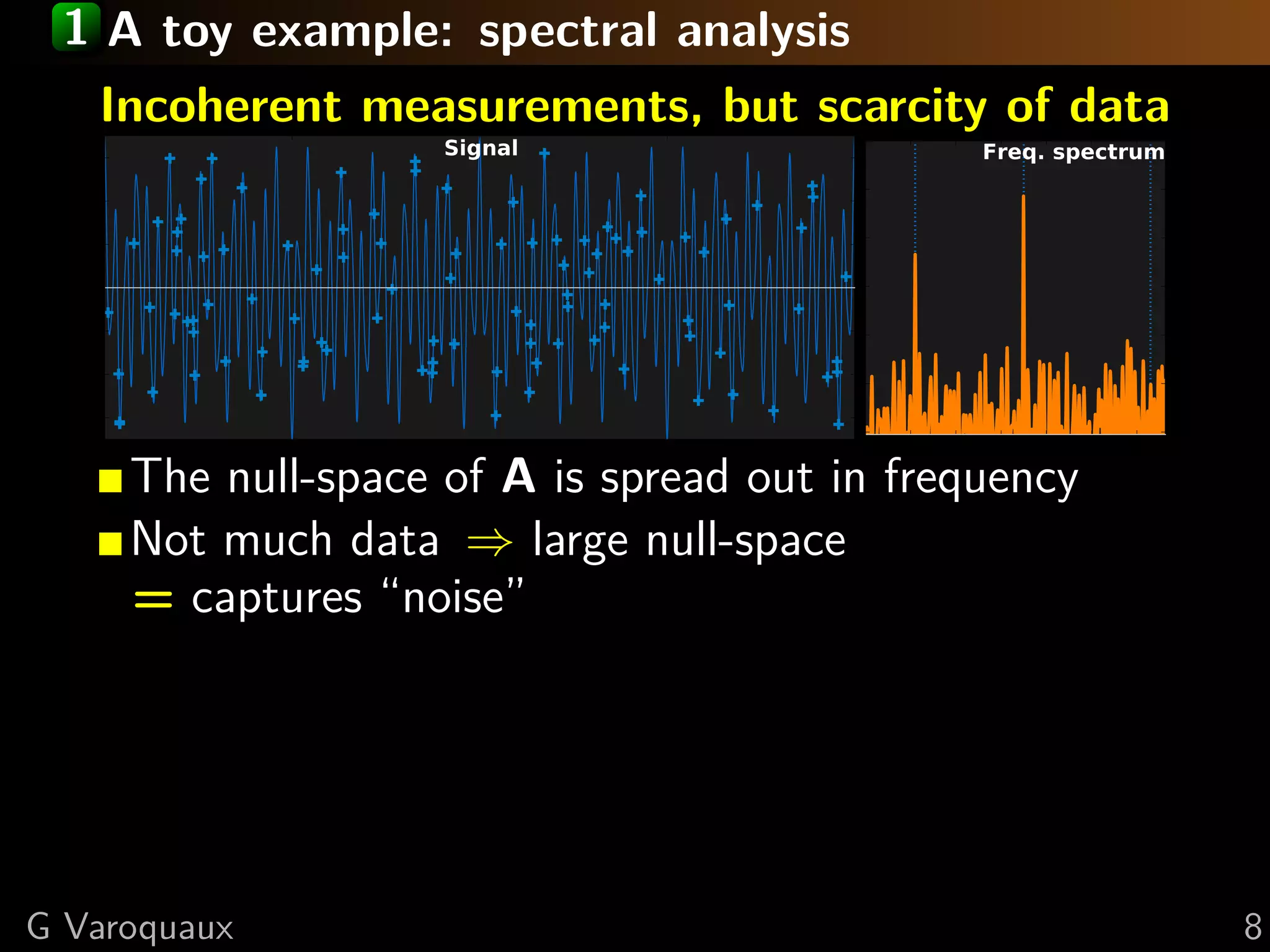
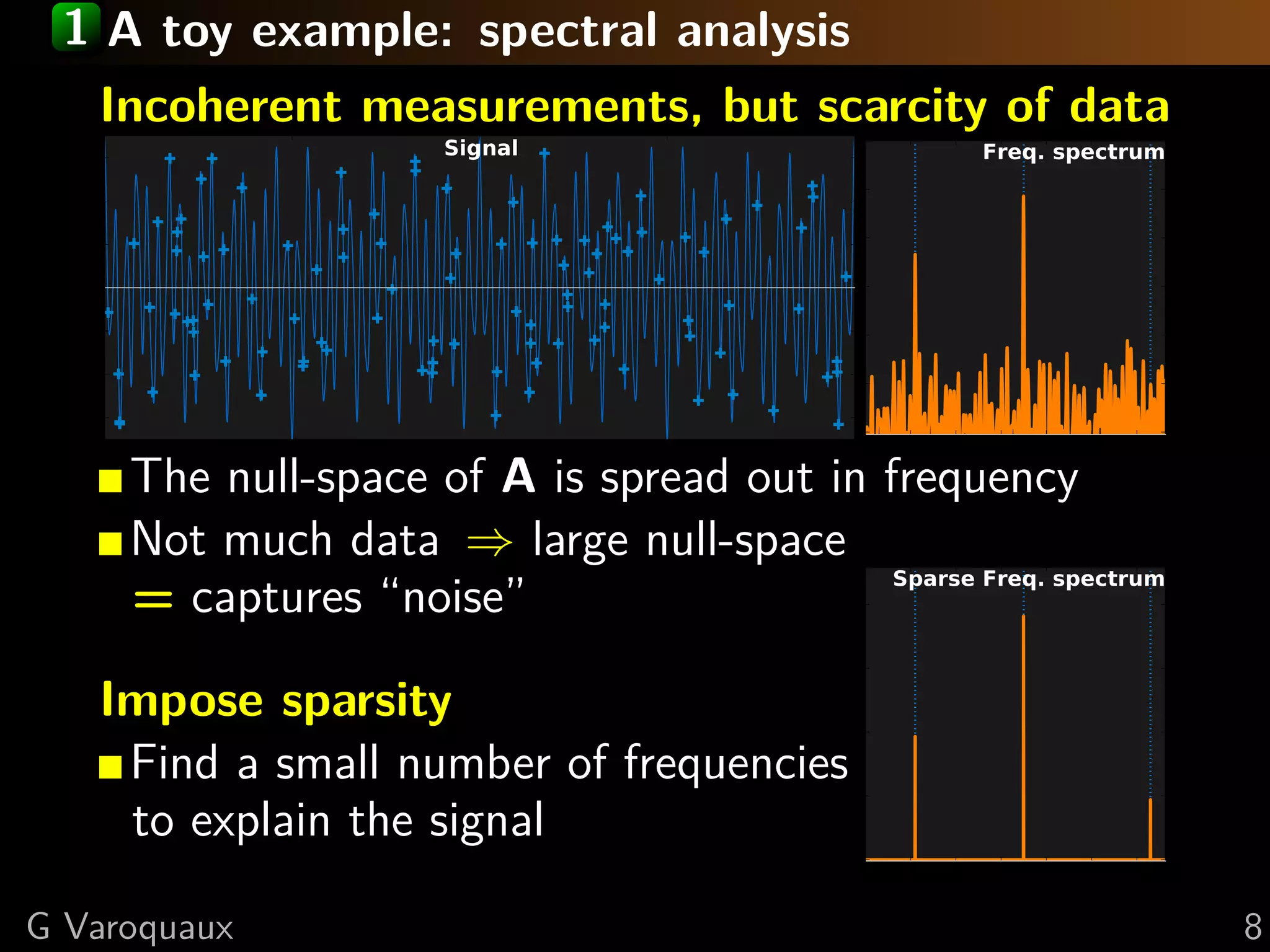
Minimum number of observations necessary:
nmin ∼ k log p, with k: number of non zeros
[Candes 2006]
Rmk Theory for i.i.d. samples
Related to “compressive sensing”
G Varoquaux 11

18. 2 Mathematical formulation
Variational formulation
Introduction of noise
G Varoquaux 12

19. 2 Maximizing the sparsity
0 number of non-zeros
min 0(x)
x
s.t. y = A x
x2
y=
Ax
xtrue
x1
“Matching pursuit” problem [Mallat, Zhang 1993]
“Orthogonal matching pursuit” [Pati, et al 1993]
Problem: Non-convex optimization
G Varoquaux 13

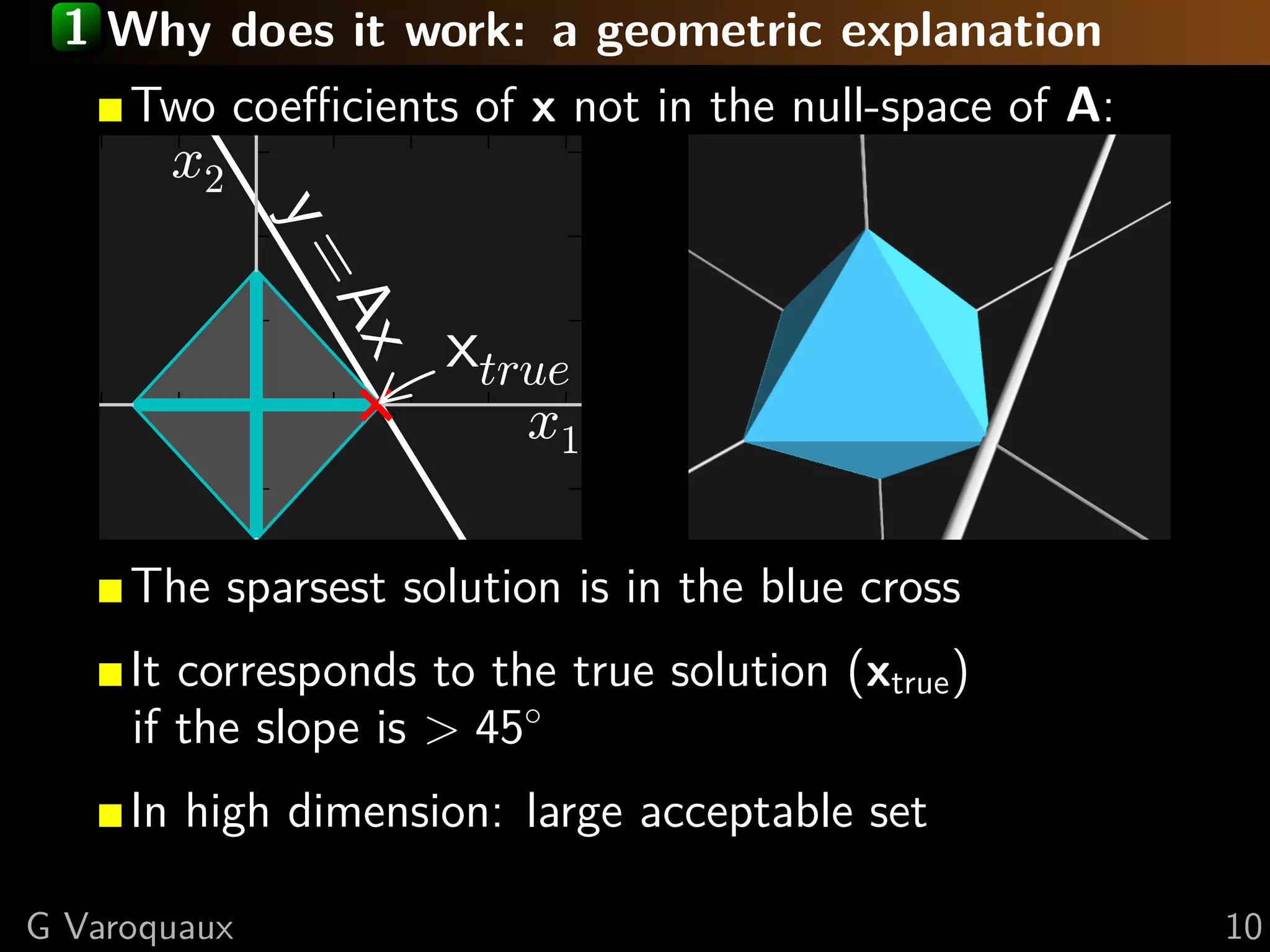
20. 2 Maximizing the sparsity
1 (x) = i |xi |
min 1(x)
x
s.t. y = A x
x2
y=
Ax
xtrue
x1
“Basis pursuit” [Chen, Donoho, Saunders 1998]
G Varoquaux 13

21. 2 Modeling observation noise
y = Ax + e e = observation noise
New formulation:
2
min 1 (x)
x
s.t. y = A x y − Ax 2 ≤ ε2
Equivalent: “Lasso estimator” [Tibshirani 1996]
2
min y − Ax
x 2 + λ 1(x)
G Varoquaux 14

22. 2 Modeling observation noise
y = Ax + e e = observation noise
New formulation:
2
min 1 (x)
x
s.t. y = A x y − Ax 2 ≤ ε2
Equivalent: “Lasso estimator” [Tibshirani 1996]
2
x2
min y − Ax
x 2 + λ 1(x)
Data fit Penalization x1
Rmk: kink in the 1 ball creates sparsity
G Varoquaux 14

23. 2 Probabilistic modeling: Bayesian interpretation
P(x|y) ∝ P(y|x) P(x) ( )
“Posterior” Forward model “Prior”
Quantity of interest Expectations on x
Forward model: y = A x + e, e: Gaussian noise
⇒ P(y|x) ∝ exp − 2 1 2 y − A x 2
σ 2
1
Prior: Laplacian P(x) ∝ exp − µ x 1
1 2 1
Negated log of ( ): 2σ 2 y − Ax 2 + µ 1 (x)
Maximum of posterior is Lasso estimate
Note that this picture is limited and the Lasso is not a good
G Varoquaux Bayesian estimator for the Laplace prior [Gribonval 2011]. 15

24. 3 Choice of a sparse
representation
Sparse in wavelet domain
Total variation
G Varoquaux 16

25. 3 Sparsity in wavelet representation
Typical images Haar decomposition
Level 1 Level 2 Level 3
are not sparse
Level 4 Level 5 Level 6
⇒ Impose sparsity in Haar representation
A → A H where H is the Haar transform
G Varoquaux 17

26. 3 Sparsity in wavelet representation
Original image Non-sparse reconstruction
Typical images Haar decomposition
Level 1 Level 2 Level 3
are not sparse
Level 4 Level 5 Level 6
Sparse image Sparse in Haar
⇒ Impose sparsity in Haar representation
A → A H where H is the Haar transform
G Varoquaux 17

27. 3 Total variation
Impose a sparse gradient
2
min y − Ax
x 2 +λ ( x)i 2
i
12 norm: 1 norm of the
gradient magnitude
Sets x and y to zero jointly
Original image Haar wavelet TV penalization
G Varoquaux 18

28. 3 Total variation
Impose a sparse gradient
2
min y − Ax
x 2 +λ ( x)i 2
i
12 norm: 1 norm of the
gradient magnitude
Sets x and y to zero jointly
Original image Error for Haar wavelet Error for TV penalization
G Varoquaux 18

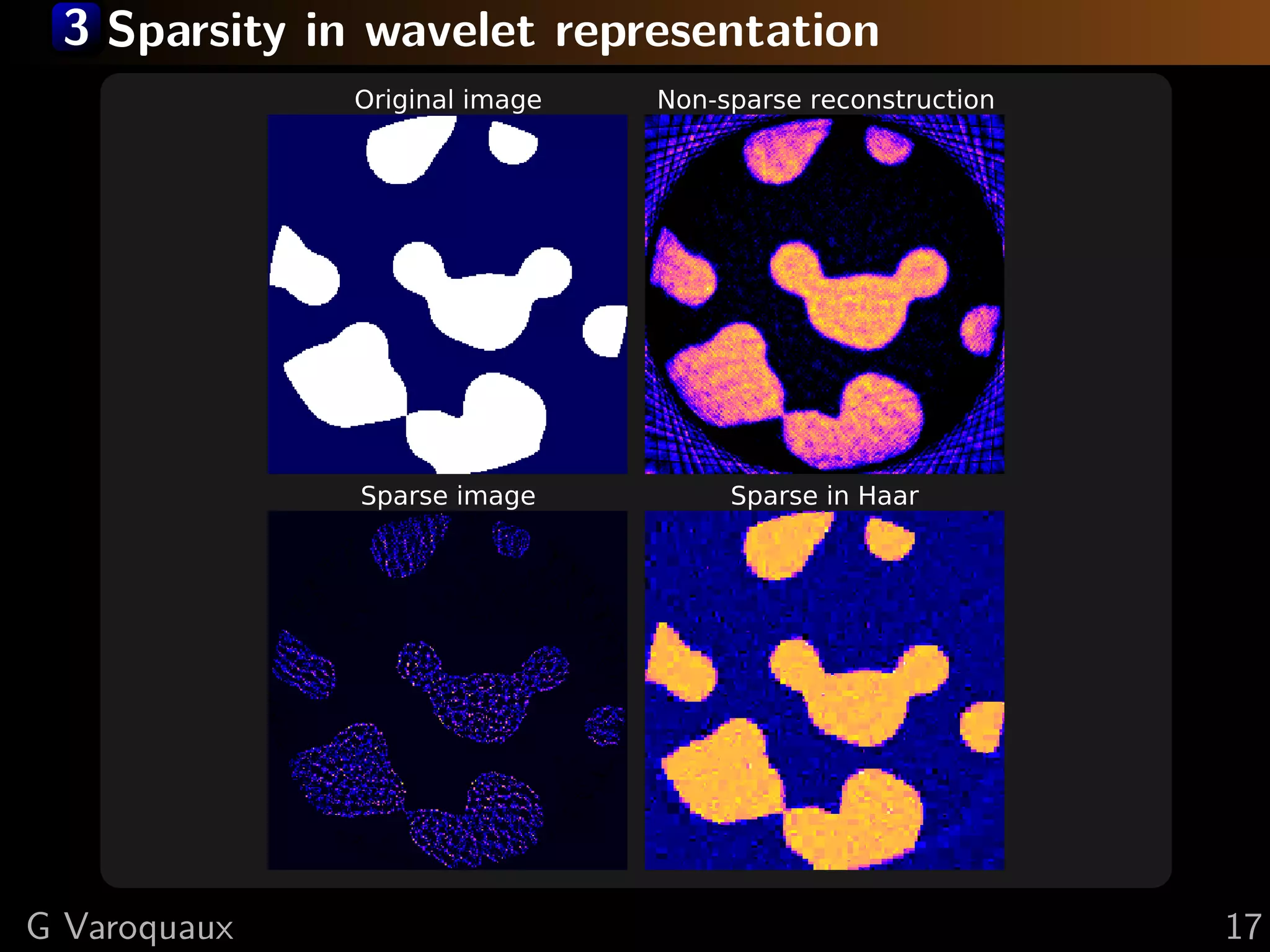
29. 3 Total variation + interval
Bound x in [0, 1]
2
min y−Ax
x 2+λ ( x)i 2 +I([0, 1])
i
Original image TV penalization TV + interval
G Varoquaux 19

30. 3 Total variation + interval
Bound x in [0, 1]
2
min y−Ax
x 2+λ ( x)i 2 +I([0, 1])
i
TV Rmk: Constraint
Histograms: TV + interval does more than fold-
ing values outside of
the range back in.
0.0 0.5 1.0
Original image TV penalization TV + interval
G Varoquaux 19

31. 3 Total variation + interval
Bound x in [0, 1]
2
min y−Ax
x 2+λ ( x)i 2 +I([0, 1])
i
TV Rmk: Constraint
Histograms: TV + interval does more than fold-
ing values outside of
the range back in.
0.0 0.5 1.0
Original image Error for TV penalization Error for TV + interval
G Varoquaux 19

32. Analysis vs synthesis
2
Wavelet basis min y − A H x 2 + x 1
H Wavelet transform
Total variation min y − A x 2 + Dx
2 1
D Spatial derivation operator ( )
G Varoquaux 20

33. Analysis vs synthesis
Wavelet basis min y − A H x 2 + x
2 1
H Wavelet transform
“synthesis” formulation
Total variation min y − A x 2 + Dx
2 1
D Spatial derivation operator ( )
“analysis” formulation
Theory and algorithms easier for synthesis
Equivalence iif D is invertible
G Varoquaux 20

34. 4 Optimization algorithms
Non-smooth optimization
⇒ “proximal operators”
G Varoquaux 21

35. 4 Smooth optimization fails!
Gradient descent
Gradient descent
x2
Energy
Iterations x1
Smooth optimization fails in non-smooth regions
These are specifically the spots that interest us
G Varoquaux 22

36. 4 Iterative Shrinkage-Thresholding Algorithm
Settings: min f + g; f smooth, g non-smooth
f and g convex, f L-Lipschitz
Typically f is the data fit term, and g the penalty
1 2 1
ex: Lasso 2σ 2 y − Ax 2 + µ 1 (x)
G Varoquaux 23

37. 4 Iterative Shrinkage-Thresholding Algorithm
Settings: min f + g; f smooth, g non-smooth
f and g convex, f L-Lipschitz
Minimize successively:
(quadratic approx of f ) + g
f (x) < f (y) + x − y, f (y)
2
+L x − y
2 2
Proof: by convexity f (y) ≤ f (x) + f (y) (y − x)
in the second term: f (y) → f (x) + ( f (y) − f (x))
upper bound last term with Lipschitz continuity of f
 
L 1 2
xk+1 = argmin g(x) + x − xk − f (xk ) 2

x 2 L
[Daubechies 2004]
G Varoquaux 23

38. 4 Iterative Shrinkage-Thresholding Algorithm
Step 1: Gradient descentsmooth, g non-smooth
Settings: min f + g; f on f
f and g convex, f L-Lipschitz
Step 2: Proximal operator of g:
Minimize proxλg (x) def argmin y − x 2 + λ g(y)
successively:
= 2
y
(quadratic approx of f ) + g
Generalization of Euclidean projection
f (x) < f (y) + x − y, f (y)1}
on convex set {x, g(x) ≤ 2 Rmk: if g is the indicator function
+L x − y 2
2
of a set S, the proximal operator
is the Euclidean projection.
Proof: by convexity f (y) ≤ f (x) + f (y) (y − x)
prox
in theλ
1
(x) = sign(x ) x − λ
second term: f (y) → f (x) + ( i f (y) − f (x))
i +
upper bound last term with Lipschitz continuity of f
“soft thresholding”
 
L 1 2
xk+1 = argmin g(x) + x − xk − f (xk ) 2

x 2 L
[Daubechies 2004]
G Varoquaux 23

39. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Gradient descent step
G Varoquaux 24

40. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Projection on 1 ball
G Varoquaux 24

41. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Gradient descent step
G Varoquaux 24

42. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Projection on 1 ball
G Varoquaux 24

43. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Gradient descent step
G Varoquaux 24

44. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Projection on 1 ball
G Varoquaux 24

45. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Gradient descent step
G Varoquaux 24

46. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
Projection on 1 ball
G Varoquaux 24

47. 4 Iterative Shrinkage-Thresholding Algorithm
Gradient descent
x2
ISTA
Energy
Iterations x1
G Varoquaux 24

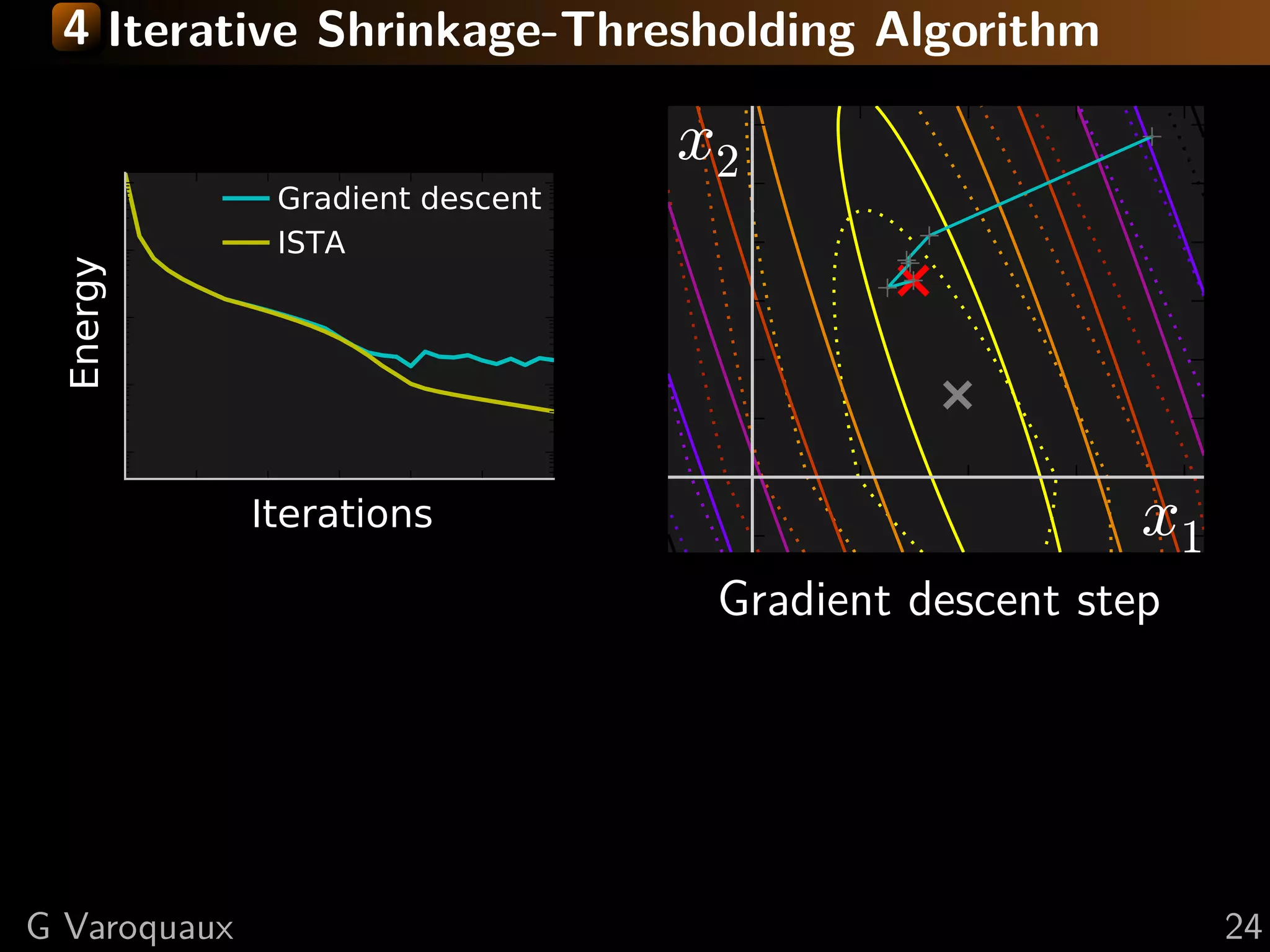
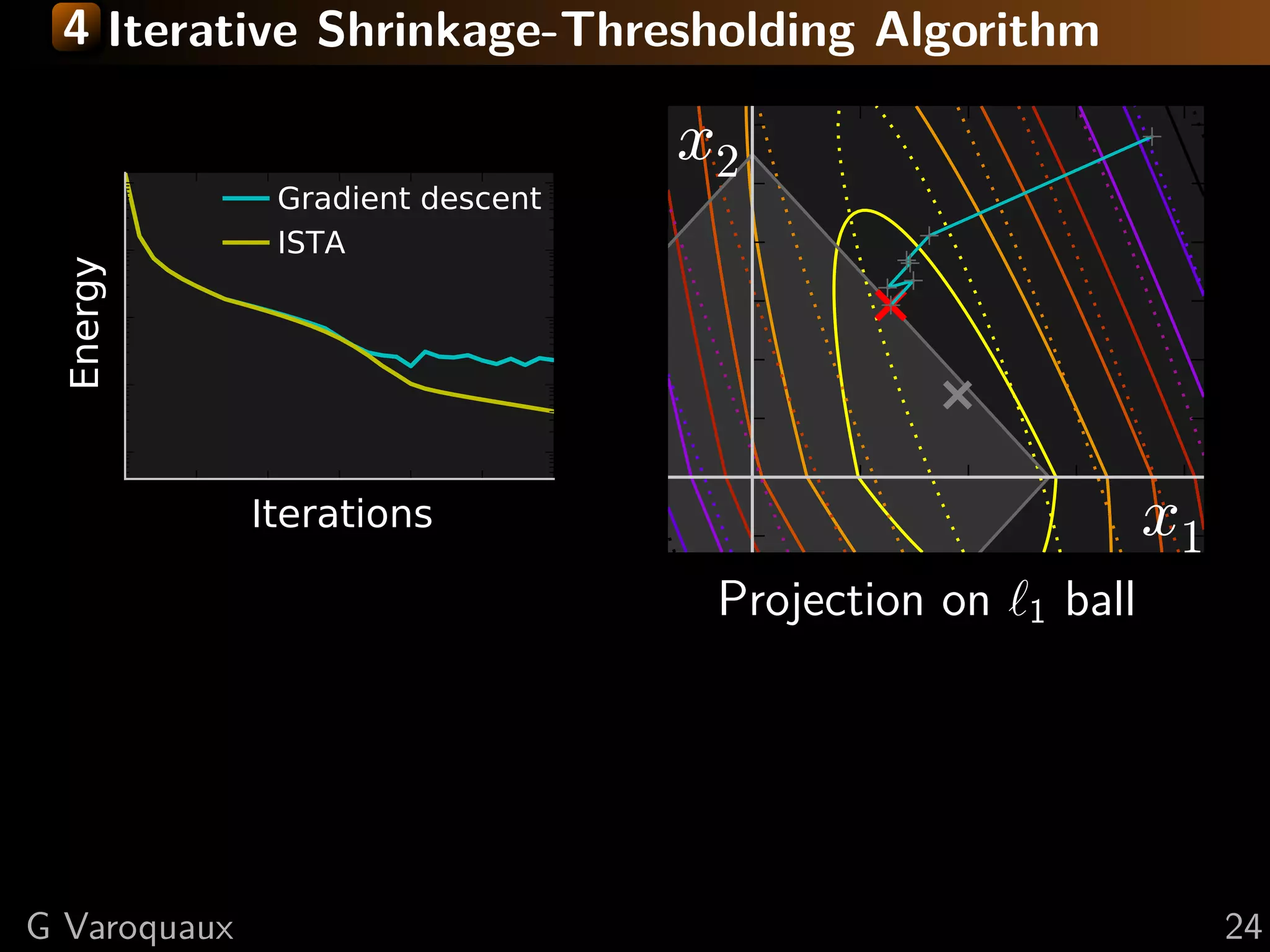
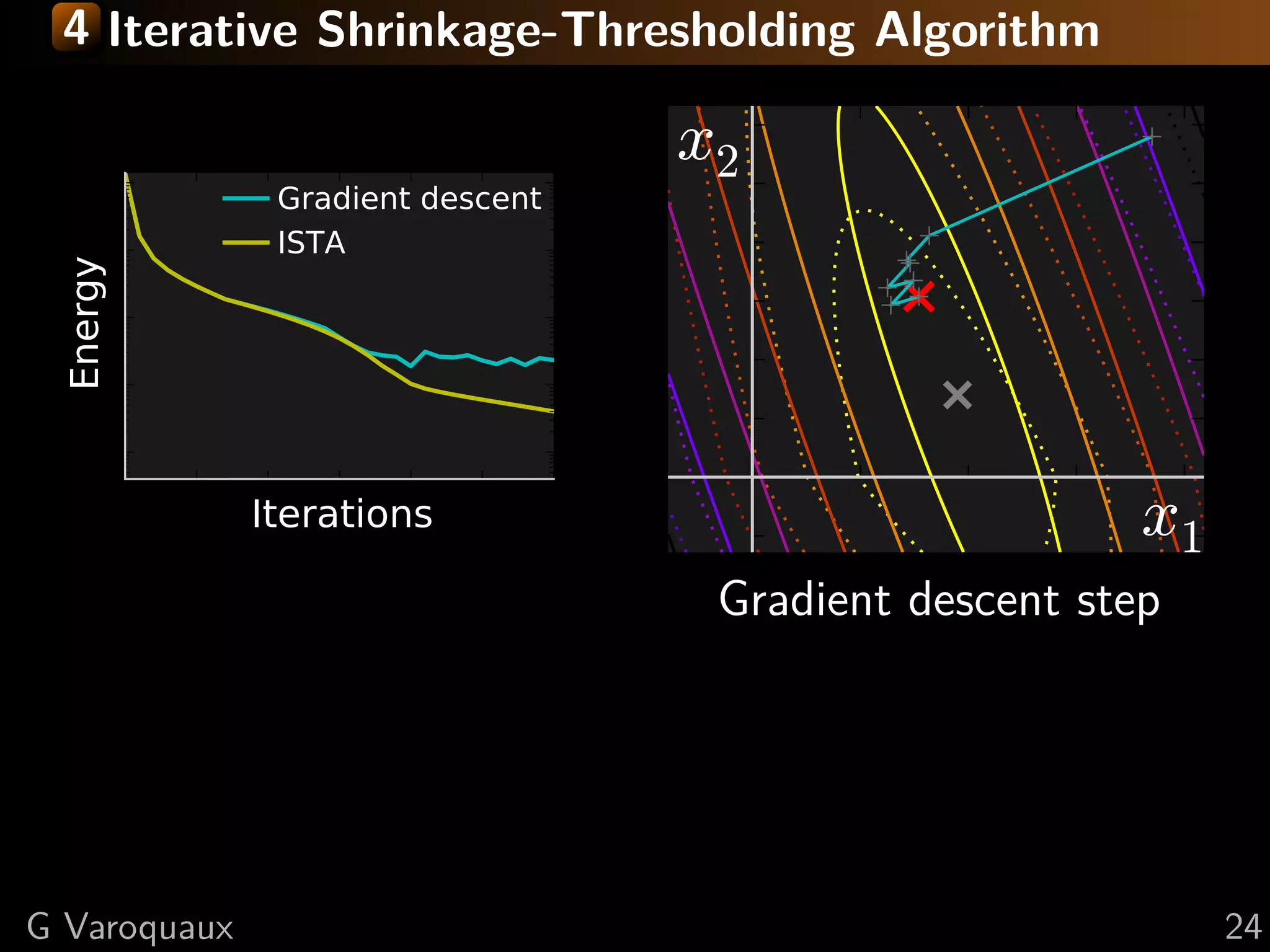
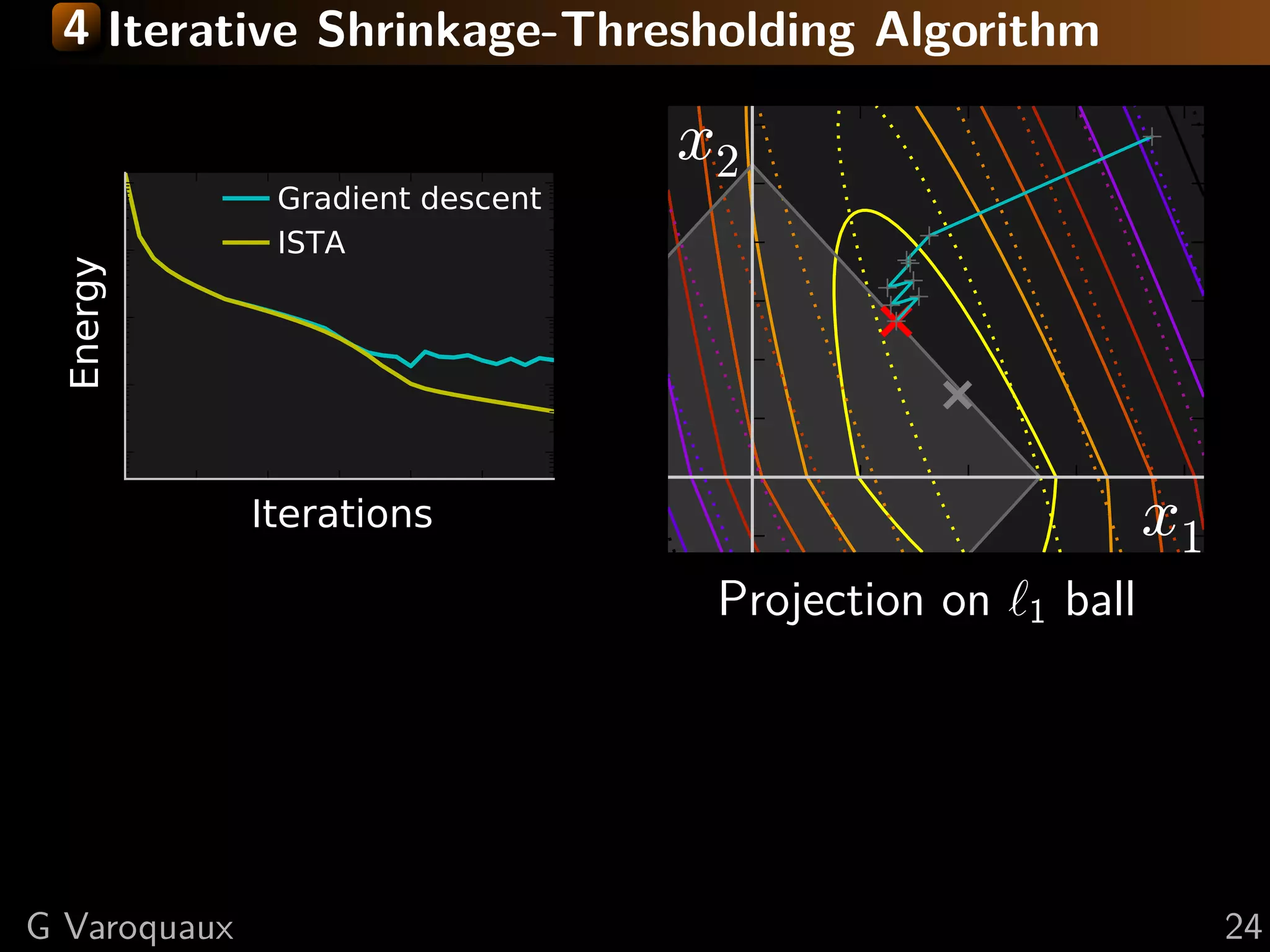
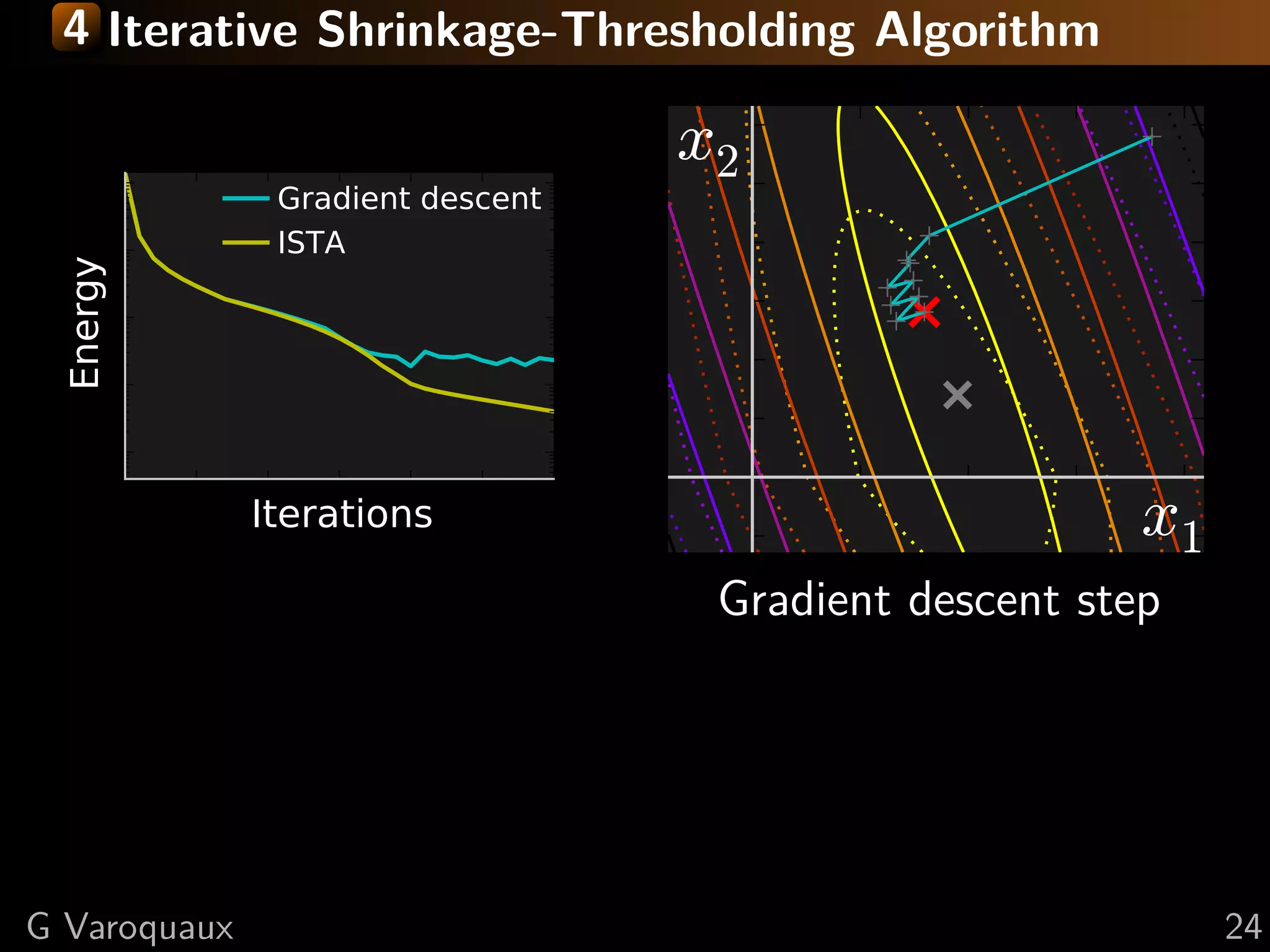
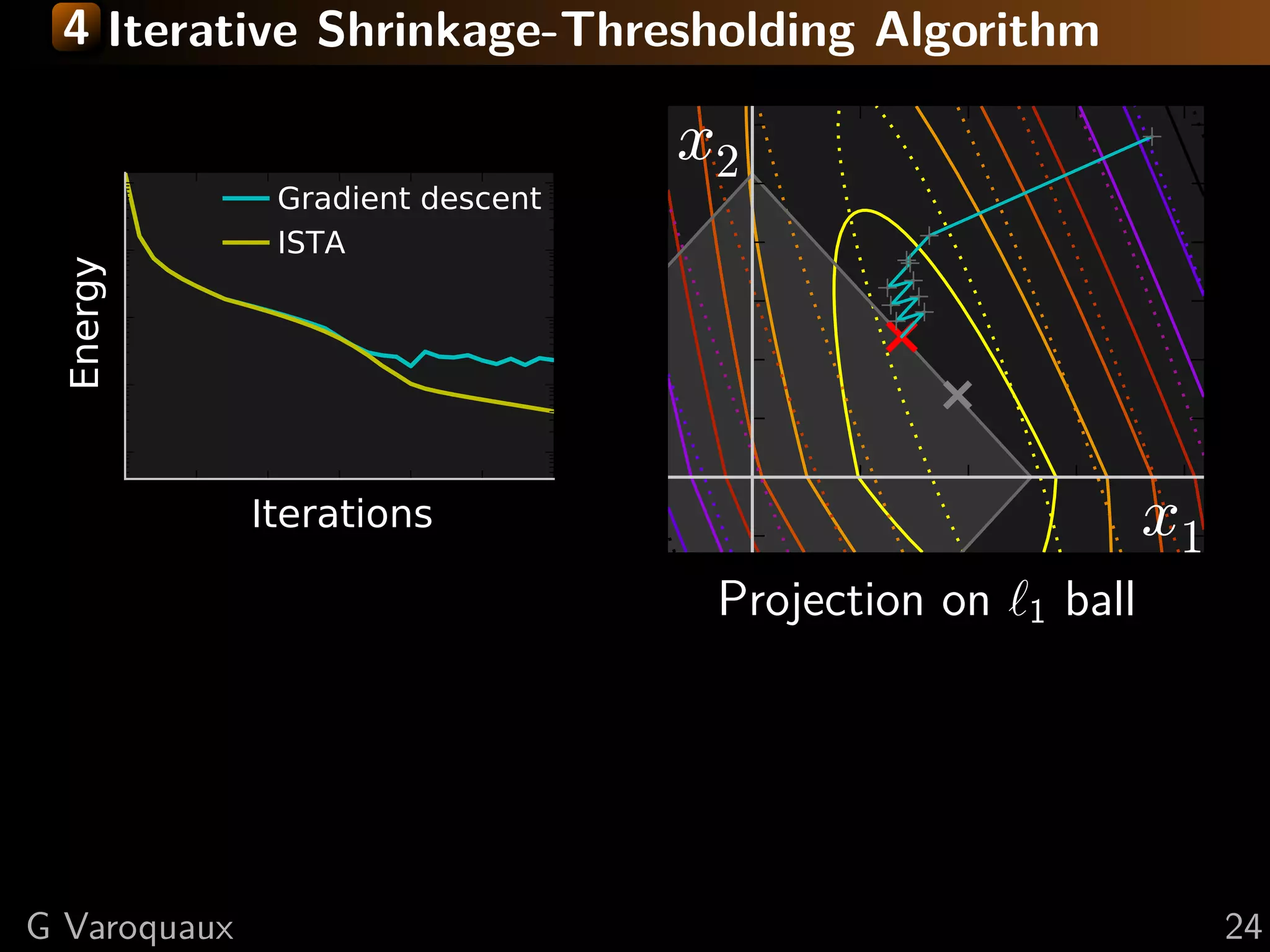
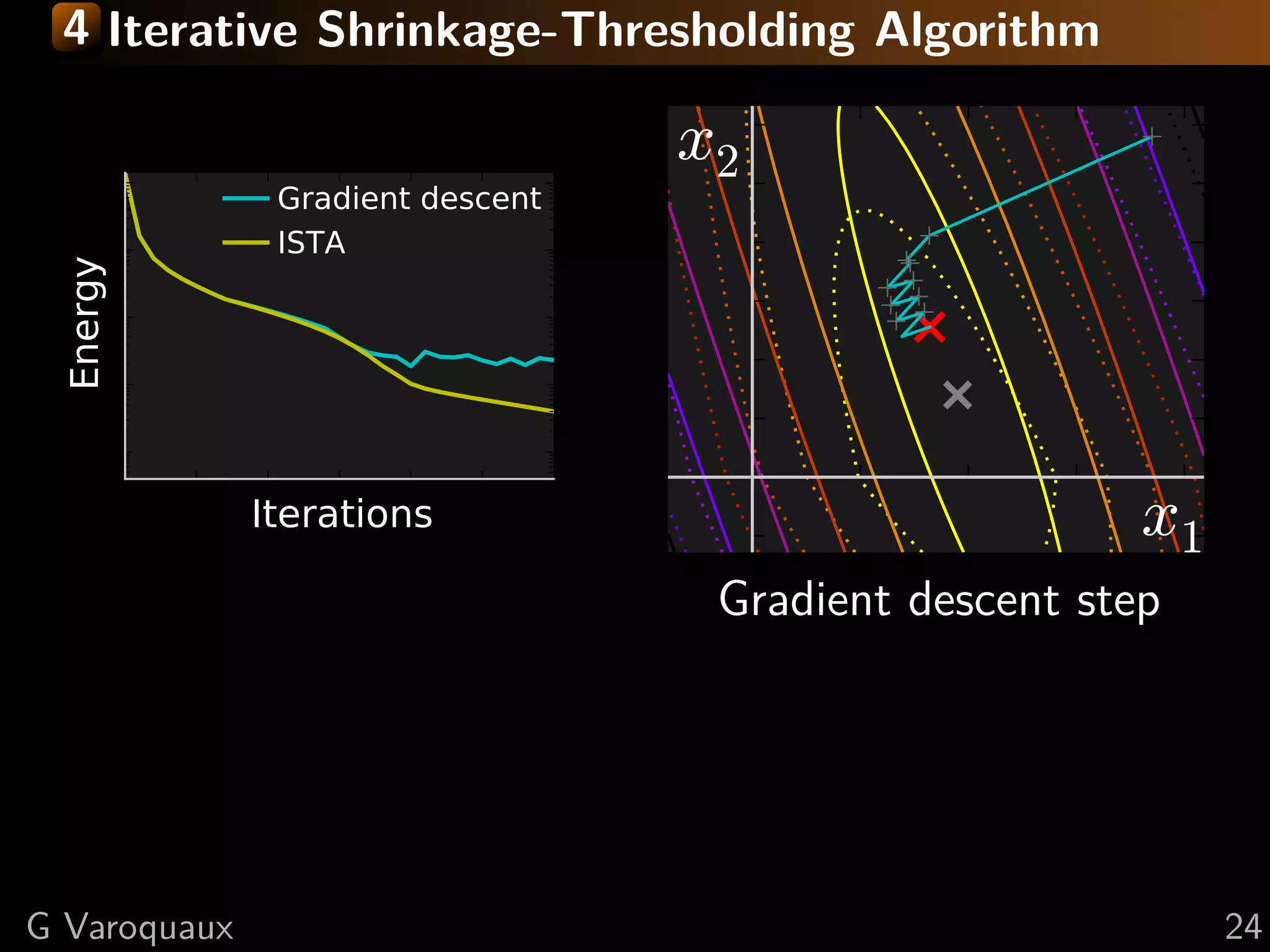
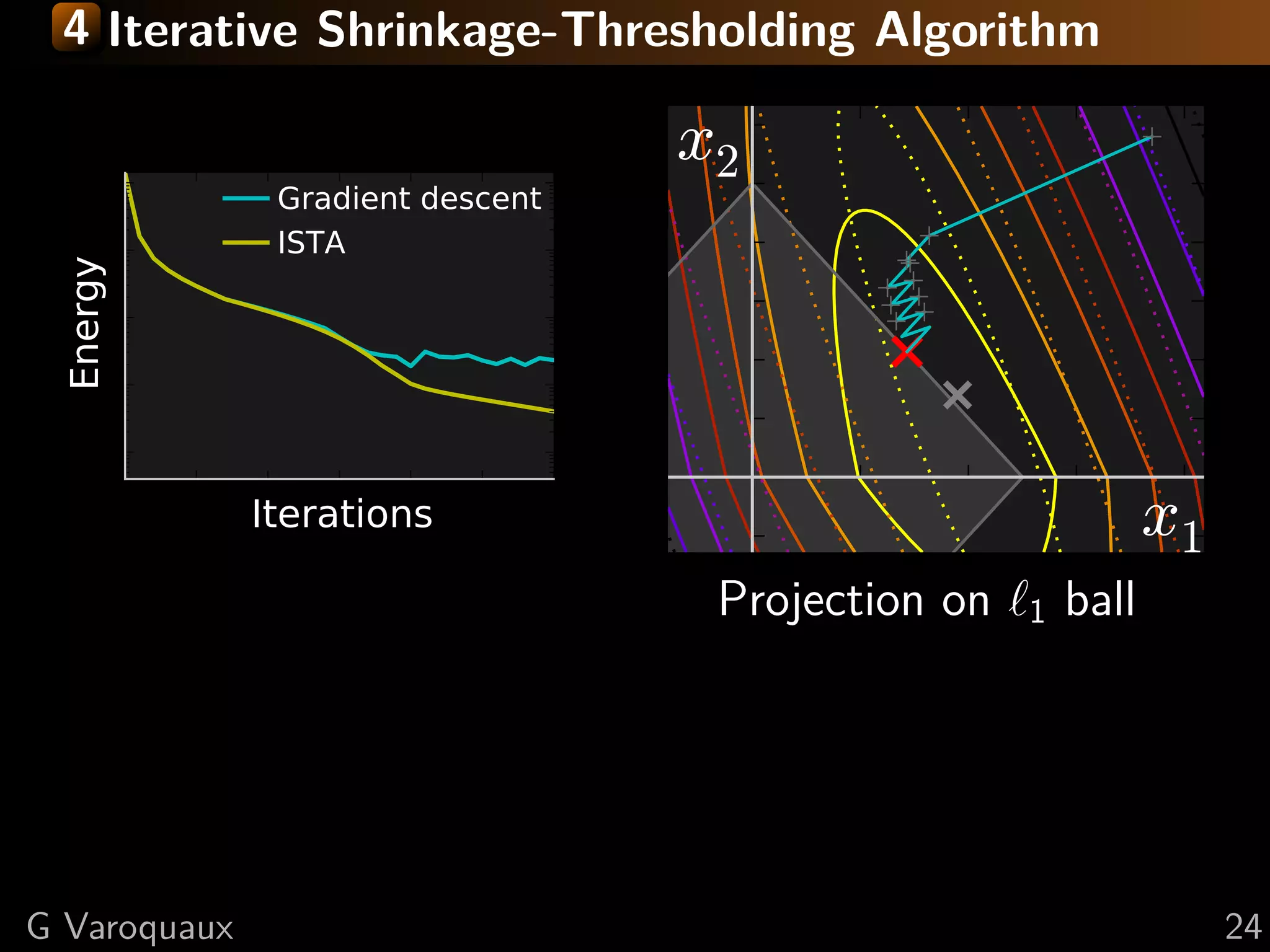
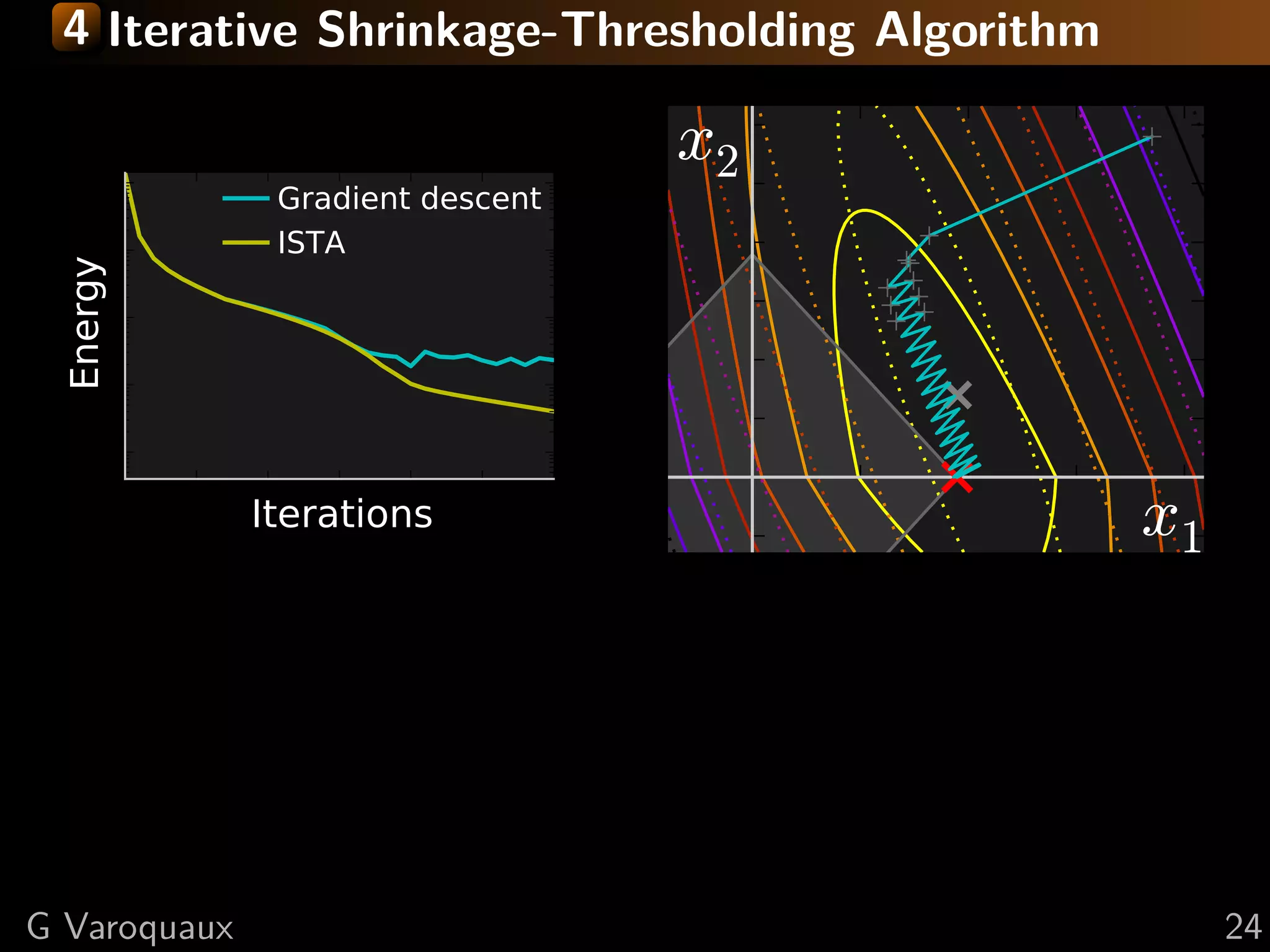
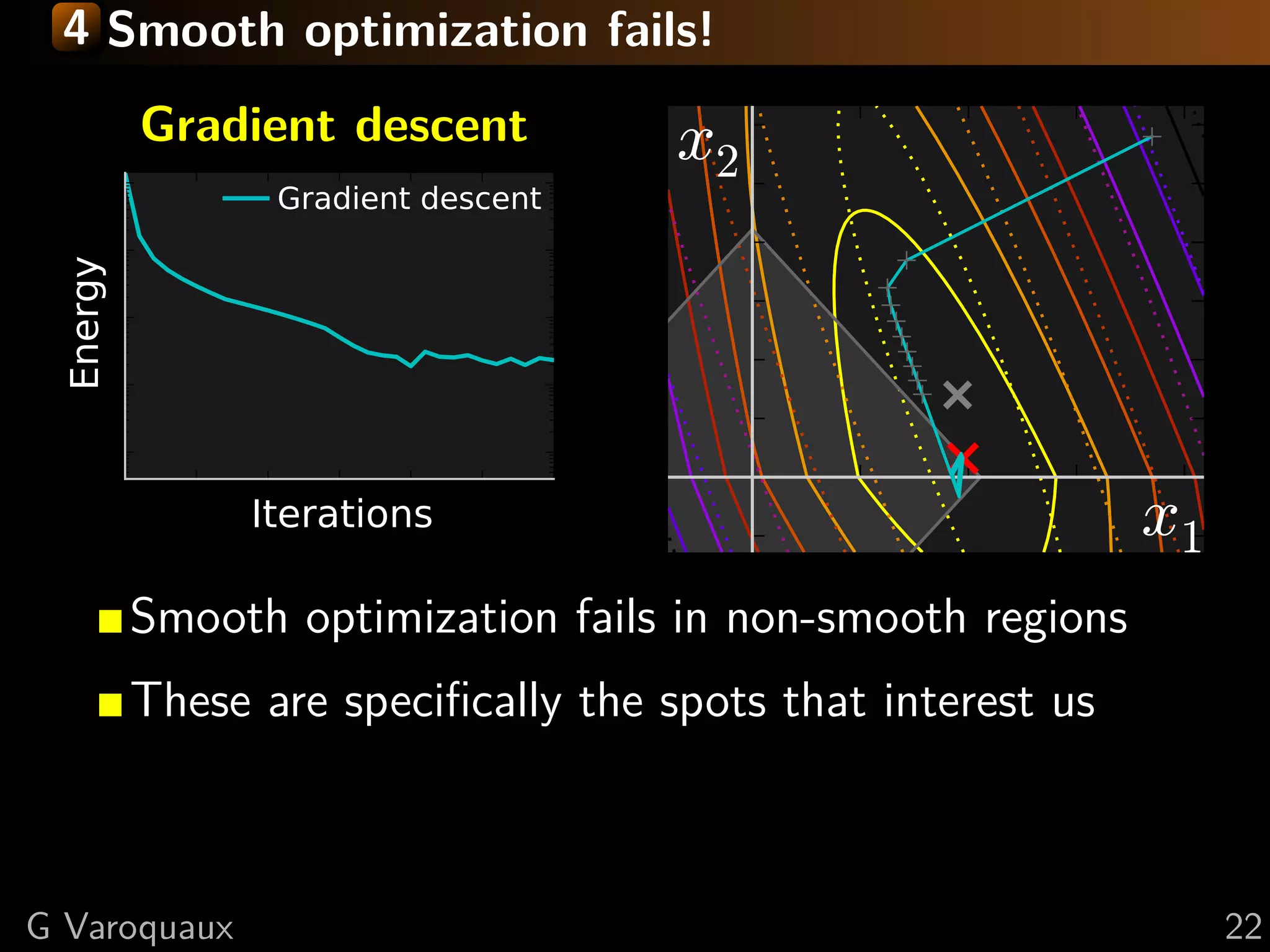
48. 4 Fast Iterative Shrinkage-Thresholding Algorithm
FISTA
Gradient descent
x2
ISTA
FISTA
Energy
Iterations x1
As with conjugate gradient: add a memory term
ISTA tk −1
dxk+1 = dxk+1 + tk+1 (dxk − dxk−1 ) √
1+ 2
1+4 tk
t1 = 1, tk+1 = 2
⇒ O(k −2 ) convergence [Beck Teboulle 2009]
G Varoquaux 25

49. 4 Proximal operator for total variation
Reformulate to smooth + non-smooth with a simple
projection step and use FISTA: [Chambolle 2004]
2
proxλTV x = argmin y − x 2 +λ ( x)i 2
x i
G Varoquaux 26

50. 4 Proximal operator for total variation
Reformulate to smooth + non-smooth with a simple
projection step and use FISTA: [Chambolle 2004]
2
proxλTV x = argmin y − x 2 +λ ( x)i 2
x i
2
= argmax λ div z + y 2
z, z ∞ ≤1
Proof:
“dual norm”: v 1 = max v, z
z ∞ ≤1
div is the adjoint of : v, z = v, −div z
Swap min and max and solve for x
Duality: [Boyd 2004] This proof: [Michel 2011]
G Varoquaux 26

51. Sparsity for compressed tomography reconstruction
@GaelVaroquaux 27

52. Sparsity for compressed tomography reconstruction
Add penalizations with kinks x2
Choice of prior/sparse representation
Non-smooth optimization (FISTA) x1
Further discussion: choice of prior/parameters
Minimize reconstruction error from degraded
data of gold-standard acquisitions
Cross-validation: leave half of the projections
and minimize projection error of reconstruction
Python code available:
https://github.com/emmanuelle/tomo-tv
@GaelVaroquaux 27

53. Bibliography (1/3)
[Candes 2006] E. Cand`s, J. Romberg and T. Tao, Robust uncertainty
e
principles: Exact signal reconstruction from highly incomplete frequency
information, Trans Inf Theory, (52) 2006
[Wainwright 2009] M. Wainwright, Sharp Thresholds for
High-Dimensional and Noisy Sparsity Recovery Using 1 constrained
quadratic programming (Lasso), Trans Inf Theory, (55) 2009
[Mallat, Zhang 1993] S. Mallat and Z. Zhang, Matching pursuits with
Time-Frequency dictionaries, Trans Sign Proc (41) 1993
[Pati, et al 1993] Y. Pati, R. Rezaiifar, P. Krishnaprasad, Orthogonal
matching pursuit: Recursive function approximation with plications to
wavelet decomposition, 27th Signals, Systems and Computers Conf 1993
@GaelVaroquaux 28

54. Bibliography (2/3)
[Chen, Donoho, Saunders 1998] S. Chen, D. Donoho, M. Saunders,
Atomic decomposition by basis pursuit, SIAM J Sci Computing (20) 1998
[Tibshirani 1996] R. Tibshirani, Regression shrinkage and selection via the
lasso, J Roy Stat Soc B, 1996
[Gribonval 2011] R. Gribonval, Should penalized least squares regression
be interpreted as Maximum A Posteriori estimation?, Trans Sig Proc,
(59) 2011
[Daubechies 2004] I. Daubechies, M. Defrise, C. De Mol, An iterative
thresholding algorithm for linear inverse problems with a sparsity
constraint, Comm Pure Appl Math, (57) 2004
@GaelVaroquaux 29

55. Bibliography (2/3)
[Beck Teboulle 2009], A. Beck and M. Teboulle, A fast iterative
shrinkage-thresholding algorithm for linear inverse problems, SIAM J
Imaging Sciences, (2) 2009
[Chambolle 2004], A. Chambolle, An algorithm for total variation
minimization and applications, J Math imag vision, (20) 2004
[Boyd 2004], S. Boyd and L. Vandenberghe, Convex Optimization,
Cambridge University Press 2004
— Reference on convex optimization and duality
[Michel 2011], V. Michel et al., Total variation regularization for
fMRI-based prediction of behaviour, Trans Med Imag (30) 2011
— Proof of TV reformulation: appendix C
@GaelVaroquaux 30