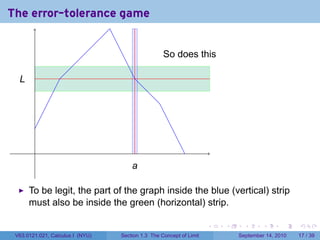
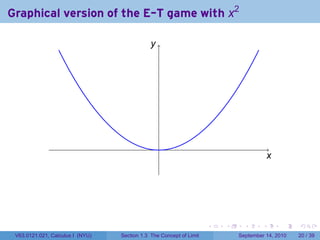
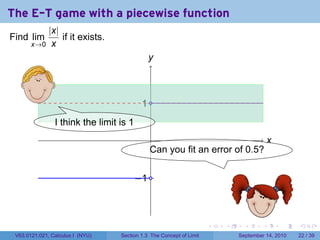
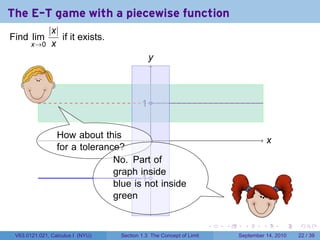
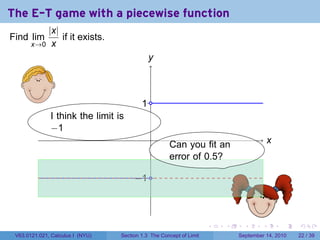
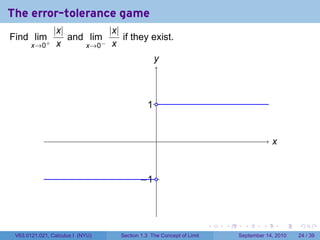
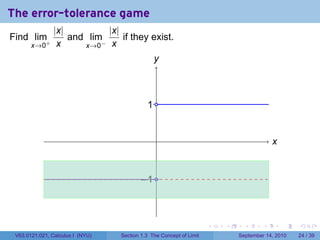
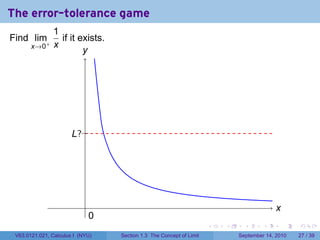
This document contains lecture notes on the concept of limit from a Calculus I course at New York University. It includes announcements about homework and deadlines. It then discusses guidelines for written homework assignments and a rubric for grading. The bulk of the document explains the concept of limit intuitively through an "error-tolerance game" and provides examples to illustrate the idea. It aims to build an informal understanding of limits before providing a precise definition.