1) Electric charge is a fundamental property of matter that comes in two types: positive and negative. Like charges repel and unlike charges attract, as described by Coulomb's Law. 2) An electric field is a physical quantity that permeates space and is created by electric charges. It exerts force on other charges and is a vector field. The electric field is proportional to the charge creating it and inversely proportional to the distance from that charge. 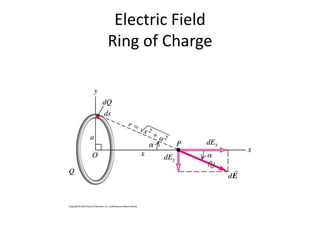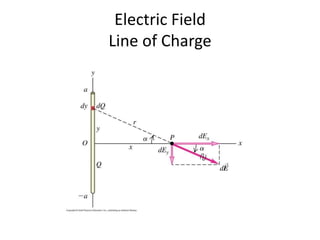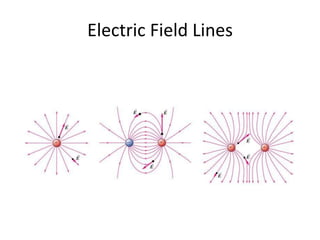3) When multiple charges are present, the net electric field is the vector sum of the individual electric fields according to the superposition principle. Electric field lines provide a pictorial representation of electric fields, with density and direction corresponding to field strength and direction.

1. Electric Charges,
Forces, and
Fields

2. Electric Charges
Electric charge is a basic property of matter
Two basic charges
Positive and Negative
Each having an absolute value of
1.6 x 10-19 Coulombs
Experiments have shown that
Like signed charges repel each other
Unlike signed charges attract each other
For an isolated system, the net charge of the system
remains constant
Charge Conservation

3. Two basics type of materials
Conductors
Materials, such as metals, that allow the free
movement of charges
Insulators
Materials, such as rubber and glass, that don’t
allow the free movement of charges

4. Coulomb’s Law
Coulomb found that the electric force between two
charged objects is
Proportional to the product of the charges on the
objects, and
Inversely proportional to the separation of the
objects squared
2
21
r
qq
kF
k being a proportionality constant, having a value
of 8.988 x 109 Nm2/c2

5. Electric Force
122
21
12 ˆr
r
qq
kF

This gives the force on charged object 2 due to charged
object 1
The direction of the force is either parallel or
antiparallel to this unit vector depending upon the
relative signs of the charges
12ˆr is a unit vector pointing from object 1 to object 2
As with all forces, the electric force is a Vector
So we rewrite Coulomb’s Law as
q2q1

6. Electric Force
The force acting on each charged object has the
same magnitude - but acting in opposite directions
(Newton’s Third Law)2112 FF


7. More Than Two Charges
q
q1
q2
qqF
1

qqF
2

netF

If q1 were the only other charge, we would
know the force on q due to q1 -
qqF
1

If q2 were the only other charge, we would
know the force on q due to q2 -
qqF
2

Given charges q, q1, and q2
What is the net force if both charges are present?
The net force is given by the Superposition Principle
21 FFFnet


8. Superposition of Forces
If there are more than two charged objects
interacting with each other
The net force on any one of the charged
objects is
The vector sum of the individual Coulomb
forces on that charged object
ji
r
r
q
kqF ij
ij
i
jj ˆ2


9. Note on constants
k is in reality defined in terms of a more
fundamental constant, known as the
permittivity of free space.
2
2
12
0
0
C
10854.8
4
1
Nm
xwith
k

10. Electric Field
The Electric Force is like the Gravitational Force
Action at a Distance
The electric force can be thought of as being
mediated by an electric field.

11. What is a Field?
A Field is something that can be defined anywhere
in space
A field represents some physical quantity
(e.g., temperature, wind speed, force)
It can be a scalar field (e.g., Temperature field)
It can be a vector field (e.g., Electric field)
It can be a “tensor” field (e.g., Space-time curvature)

12. 77
82
83
68
55
66
83
75 80
90
91
75
71
80
72
84
73
82
88
92
77
88
88
73
64
A Scalar Field
A scalar field is a map of a quantity that has only
a magnitude, such as temperature

13. 77
82
83
68
55
66
83
75 80
90
91
75
71
80
72
84
73
57
88
92
77
56
88
7364
A Vector Field
A vector field is a map of a quantity that is a
vector, a quantity having both magnitude
and direction, such as wind

14. Electric Field
We say that when a charged object is put at a
point in space,
The charged object sets up an Electric Field
throughout the space surrounding the
charged object
It is this field that then exerts a force on
another charged object

15. Electric Field
Like the electric force,
the electric field is also a vector
If there is an electric force acting on an object
having a charge qo, then the electric field at
that point is given by
0q
F
E


(with the sign of q0 included)

16. Electric Field
The force on a positively
charged object is in the same
direction as the electric field at
that point,
While the force on a negative
test charge is in the opposite
direction as the electric field
at the point

17. Electric Field
A positive charge sets up
an electric field pointing
away from the charge
A negative charge sets up an
electric field pointing towards
the charge

18. Electric Field
r
r
q
kE ˆ2

The electric field of a point charge can then be
shown to be given by
ji
r
r
q
k ij
ij
i
jj qF ˆ2
Earlier we saw that the
force on a charged object
is given by
The term in parentheses remains the same if we
change the charge on the object at the point in
question
The quantity in the parentheses can be thought of as the electric field at the
point where the test object is placed

19. Electric Field
As with the electric force, if there are several
charged objects, the net electric field at a
given point is given by the vector sum of the
individual electric fields
i
iEE


20. Electric Field
r
r
dq
kE ˆ2

If we have a continuous charge distribution the
summation becomes an integral

21. Hints
1) Look for and exploit symmetries in the
problem.
2) Choose variables for integration carefully.
3) Check limiting conditions for appropriate
result

22. Electric Field
Ring of Charge

23. Electric Field
Line of Charge

24. Two equal, but opposite charges are placed on the x axis. The positive charge is placed at
x = -5 m and the negative charge is placed at x = +5m as shown in the figure above.
1) What is the direction of the electric field at point A?
a) up b) down c) left d) right e) zero
2) What is the direction of the electric field at point B?
a) up b) down c) left d) right e) zero
Example

25. Example
Two charges, Q1 and Q2, fixed along the x-axis as
shown produce an electric field, E, at a point
(x,y) = (0,d) which is directed along the negative
y-axis.
Which of the following is true?
Q2
Q1
(c) E
Q2
Q1
(b)
E
Q2
Q1 x
y
Ed
(a) Both charges Q1 and Q2 are positive
(b) Both charges Q1 and Q2 are negative
(c) The charges Q1 and Q2 have opposite signs
E
Q2
Q1
(a)

26. Electric Field Lines
Possible to map out the electric field in a region
of space
An imaginary line that at any given point has
its tangent being in the direction of the electric
field at that point
The spacing, density, of lines is related to the
magnitude of the electric field at that point

27. Electric Field Lines
At any given point, there can be only one field
line
The electric field has a unique direction at any
given point
Electric Field Lines
Begin on Positive Charges
End on Negative Charges

28. Electric Field Lines

29. Electric Dipole
An electric dipole is a pair of point charges having equal
magnitude but opposite sign that are separated by a
distance d.
Two questions concerning dipoles:
1) What are the forces and torques acting on a dipole
when placed in an external electric field?
2) What does the electric field of a dipole look like?

30. Force on a Dipole
Given a uniform external field
Then since the charges are of equal
magnitude, the force on each charge has
the same value
However the forces are in opposite directions!
Therefore the net force on the dipole is
Fnet = 0

31. Potential Energy of a Dipole
Given a dipole in an external field:
Dipole will rotate due to torque
Electric field will do work
The work done is the negative of the
change in potential energy of the dipole
The potential energy can be shown to be
EdqU


32. Electric Field of a Dipole