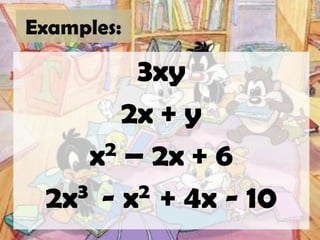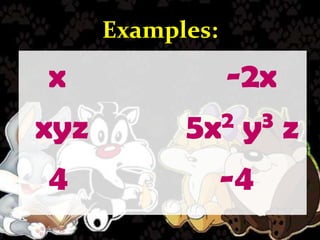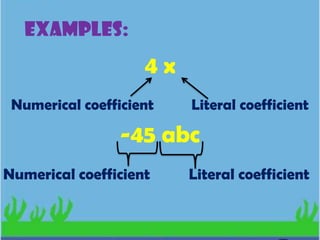
The document defines key concepts for classifying algebraic expressions, including: - Monomials have one term, binomials have two terms, and trinomials have three terms. - The degree of a polynomial with one variable is the highest exponent, and with multiple variables it is the highest sum of exponents. - A polynomial can be classified by the number of terms and its degree. The leading coefficient is the coefficient of the highest degree term.

1. CLASSIFYING ALGEBRAIC EXPRESSIONS

2. REVIEW/DRILL:Translate the given Algebraic Expression to English Phrase.6m – 5x + y + z3(ab)

3. REVIEW/DRILL:Translate the given Algebraic Expression to English Phrase.5m2n3x + y

4. REVIEW/DRILL:Translate the given Algebraic Expression to English Phrase.25 + ab3 (m + n)_1_x 4

5. Define:“mono”“bi”“tri”“poly”

6. Define the word “mono”CLUE:

7. Define the word “bi”CLUE:

8. Define the word “tri”CLUE:

9. Define the word “poly”CLUE:

10. POLYNOMIALan algebraic expression that represents a sum of ONE or MORE TERMS containing whole number exponents on the variables

11. Remember the parts of a term?

12. NUMERICAL COEFFICIENTThe number in an algebraic term.LITERAL COEFFICIENTA letter used to represent a numberEXAMPLES:4 xNumerical coefficient Literal coefficient45 abc Numerical coefficient Literal coefficient

13. Examples:3xy2x + yx2 – 2x + 62x3 - x2 + 4x - 10

14. NOT A POLYNOMIALVariable inside the radical sign√ 3x4x + √ 7y5a – 3b + √ c

15. NOT A POLYNOMIALNegative exponents.2x + y -23x4 y-1 z3m-3 + 8

16. NOT A POLYNOMIALVariable in the denominator__2x + y__z__1__2x

17. NOT A POLYNOMIAL..If there is/are….Variable/s inside the radical signNegative exponent/s.Variable/s in the denominator

18. CLASSIFICATION OF POLYNOMIALS:MonomialBinomialTrinomial

19. MONOMIALa polynomial with ONE TERM

20. Examples:x -2x xyz 5x2 y3 z 4 -4

21. BINOMIALa polynomial with TWO TERMS

22. Examples:x + y 2x – 3y 4a + b2 a3 – bc2d-3m – n m + _1_ 2

23. TRINOMIALa polynomial with THREETERMS

24. Examples:x + y + z2x – 3y – 4za3 – 4b + c4

25. Classify the following polynomials:1) binomial2) monomial3) Trinomial4) monomial5) NOT a polynomial1) 2x + 32) a2 b45x – 3y + 4z -8 3a – 2b -3

26. REVIEW:What is a polynomial? How can we differentiate a polynomial from not a polynomial?What are the two parts of a term?What are the classifications of a polynomial? Differentiate each classification.

27. DEGREE of a polynomial:The DEGREE of a term that has only one variable is the EXPONENT of that variable.Examples:

28. DEGREE of a polynomial:The DEGREEof a polynomial that has only one variable is the HIGHEST EXPONENTappearing in any of the terms.Examples:

29. DEGREE of a polynomial:The DEGREE of a term that has only one variable is the EXPONENT of that variable.Examples:

30. DEGREE of a polynomial:The DEGREE of a polynomial in more than one variable is the highest sum of the exponentsExamples:

31. Polynimial is written in desccendingorder, the coefficient of the first term is the leading coefficient.

32. 5x + 3x2 – 7Polynomial or not a Polynomial: PolynomialClassification: TrinomialDescending order: 3x2 + 5x - 7Degree:Leading Coefficient: 23

33. -5x3 + 12/x2 + 4x + 9Polynomial or not a Polynomial:Classification:Descending order:Degree: 2Leading Coefficient:

34. 8x5 y3 – 5x4 y6 + 6x3 y4Polynomial or not a Polynomial:Classification:Descending order:Degree: Leading Coefficient: