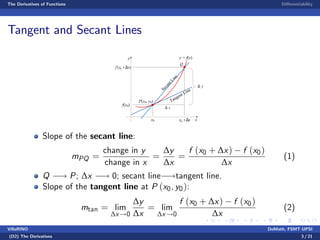
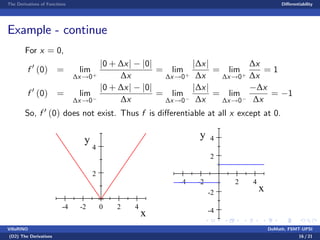
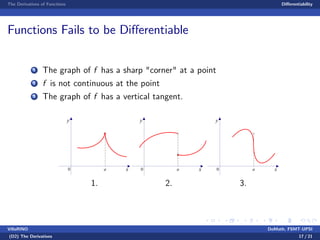
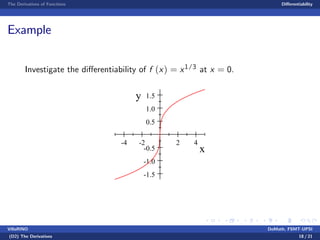
- The document discusses the concept of derivatives in calculus, including definitions, notations, and methods for computing derivatives of functions. - It provides examples of computing derivatives of various functions like polynomials, square roots, and rational functions. - A function is said to be differentiable if its derivative exists, and the document explores conditions where a function may not be differentiable, such as having a sharp corner or vertical tangent.

1. Beginning Calculus
- The Derivatives -
Shahrizal Shamsuddin Norashiqin Mohd Idrus
Department of Mathematics,
FSMT - UPSI
(LECTURE SLIDES SERIES)
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 1 / 21

2. The Derivatives of Functions Di¤erentiability
Learning Outcomes
Compute the slopes of secant and tangent lines.
Evaluate the derivative of functions using limits.
Determine the di¤erentiability of a function.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 2 / 21

3. The Derivatives of Functions Di¤erentiability
Tangent and Secant Lines
y
x
f(x0)
x0
P(x0, y0) Tangent Line
SecantLine
y = f(x)
Q
)( 0 xxf ∆+
y∆
x∆
xx ∆+0
Slope of the secant line:
mPQ =
change in y
change in x
=
∆y
∆x
=
f (x0 + ∆x) f (x0)
∆x
(1)
Q ! P; ∆x ! 0; secant line !tangent line.
Slope of the tangent line at P (x0, y0):
mtan = lim
∆x!0
∆y
∆x
= lim
∆x!0
f (x0 + ∆x) f (x0)
∆x
(2)
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 3 / 21

4. The Derivatives of Functions Di¤erentiability
Example
The equation of the tangent line to the parabola f (x) = x2 at the
point (1, 1) is
y y0 = mtan (x x0)
mtan = lim
∆x!0
f (1 + ∆x) f (1)
∆x
= lim
∆x!0
(1 + ∆x)2
1
∆x
= lim
∆x!0
∆x2 + 2∆x
∆x
= lim
∆x!0
∆x (∆x + 2)
∆x
= lim
∆x!0
(∆x + 2) = 2
So, the equation of the tangent line is
y 1 = 2 (x 1)
y = 2x 1
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 4 / 21

5. The Derivatives of Functions Di¤erentiability
Rate of Change
The di¤erence quotient
4y
4x
=
f (x0 + ∆x) f (x0)
∆x
(3)
is called the average rate of change of y with respect to x at
x = x0.
The instantaneous rate of change of y with respect to x at
x = x0 is
lim
4x!0
4y
4x
= lim
4x!0
f (x0 + ∆x) f (x0)
∆x
(4)
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 5 / 21

6. The Derivatives of Functions Di¤erentiability
The Derivatives
The derivative of y = f (x) at x = x0 is
f 0
(x0) = lim
4x!0
4y
4x
= lim
4x!0
f (x0 + ∆x) f (x0)
∆x
(5)
provided that the limit exists.
The derivative of y = f (x) (at any x in the domain) is
f 0
(x) = lim
4x!0
4y
4x
= lim
4x!0
f (x + ∆x) f (x)
∆x
(6)
provided that the limit exists. f 0 (x) is called the derivative
function of f .
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 6 / 21

7. The Derivatives of Functions Di¤erentiability
Derivative Notations
The derivative of y = f (x) can be denoted as follows:
y0
= f 0
(x) =
dy
dx
=
df
dx
=
d
dx
(y) =
d
dx
f (x) (7)
The symbol
dy
dx
was introduced by Leibniz.
dy
dx
= lim
4x!0
4y
4x
(8)
In Leibniz notation, we use the notation
dy
dx x=x0
or
dy
dx x=x0
(9)
to indicate f 0 (x0).
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 7 / 21

8. The Derivatives of Functions Di¤erentiability
Example
Di¤erentiate y = x2 8x + 9 at x = 2.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 8 / 21

9. The Derivatives of Functions Di¤erentiability
Example
Let f (x) = x2. Then,
f 0
(x) = lim
∆x!0
f (x + ∆x) f (x)
∆x
= lim
∆x!0
(x + ∆x)2
x2
∆x
= lim
∆x!0
x2 + 2x∆x + ∆x2 x2
∆x
= lim
∆x!0
∆x (2x + ∆x)
∆x
= lim
∆x!0
(2x + ∆x) = 2x
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 9 / 21

10. The Derivatives of Functions Di¤erentiability
Example
Let f (x) = x3 x. The derivative of f is:
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 10 / 21

11. The Derivatives of Functions Di¤erentiability
Example
Let f (x) =
p
x. Then, f 0 (x) is:
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 11 / 21

12. The Derivatives of Functions Di¤erentiability
Example
Let f (x) =
1 x
2 + x
. Then, f 0 (x) is:
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 12 / 21

13. The Derivatives of Functions Di¤erentiability
Example
Let y =
1
x
. Then,
d
dx
1
x
= lim
∆x!0
1
x + ∆x
1
x
∆x
= lim
∆x!0
x x ∆x
x2∆x + x (∆x)2
= lim
∆x!0
∆x
∆x (x2 + x∆x)
= lim
∆x!0
1
x2 + x∆x
=
1
x2
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 13 / 21

14. The Derivatives of Functions Di¤erentiability
Di¤erentiability
De…nition 1
A function f is di¤erentiable at x0 if f 0 (x0) exists. It is di¤erentiable
on an open interval (a, b) (or (b, ∞) or ( ∞, a) or ( ∞, ∞) ) if it is
di¤erentiable at every number in the interval.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 14 / 21

15. The Derivatives of Functions Di¤erentiability
Example
Where is the function f (x) = jxj di¤erentiable?
For x > 0, then jxj = x, and jx + ∆xj = x + ∆x. So,
f 0
(x) = lim
∆x!0
jx + hj jxj
h
= lim
∆x!0
x + ∆x x
∆x
= 1
and so f is di¤erentiable for any x > 0. For x < 0, we have jxj = x
and jx + ∆xj = (x + ∆x) . So,
f 0
(x) = lim
∆x!0
jx + ∆xj jxj
∆x
= lim
∆x!0
(x + ∆x) ( x)
∆x
= 1
and also di¤erentiable for any x < 0.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 15 / 21

16. The Derivatives of Functions Di¤erentiability
Example - continue
For x = 0,
f 0
(0) = lim
∆x!0+
j0 + ∆xj j0j
∆x
= lim
∆x!0+
j∆xj
∆x
= lim
∆x!0+
∆x
∆x
= 1
f 0
(0) = lim
∆x!0
j0 + ∆xj j0j
∆x
= lim
∆x!0
j∆xj
∆x
= lim
∆x!0
∆x
∆x
= 1
So, f 0 (0) does not exist. Thus f is di¤erentiable at all x except at 0.
-4 -2 0 2 4
2
4
x
y
-4 -2 2 4
-4
-2
2
4
x
y
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 16 / 21

17. The Derivatives of Functions Di¤erentiability
Functions Fails to be Di¤erentiable
1 The graph of f has a sharp "corner" at a point
2 f is not continuous at the point
3 The graph of f has a vertical tangent.
y
xa0
1.
y
xa0
2.
y
xa0
3.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 17 / 21

18. The Derivatives of Functions Di¤erentiability
Example
Investigate the di¤erentiability of f (x) = x1/3 at x = 0.
-4 -2 2 4
-1.5
-1.0
-0.5
0.5
1.0
1.5
x
y
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 18 / 21

19. The Derivatives of Functions Di¤erentiability
Example - continue
The function has a vertical tangent at x = 0. Thus, the function fails to
have a derivative at x = 0. We can show this algebraically:
f 0
(0) = lim
∆x!0
f (0 + ∆x) f (0)
∆x
= lim
∆x!0
(∆x)1/3
0
∆x
= lim
∆x!0
1
(∆x)2/3
As ∆x ! 0, the denominator becomes small, so the function grows
without bound. This continuous function is di¤erentiable everywhere
except at x = 0.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 19 / 21

20. The Derivatives of Functions Di¤erentiability
Di¤erentiable Implies Continuous
Theorem 2
If f (x) is a di¤erentiable at a, then f (x) is continuous at a.
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 20 / 21

21. The Derivatives of Functions Di¤erentiability
Proof:
Let f (x) be a di¤erentiable function at x = a. Then,
f 0
(a) = lim
x!a
f (x) f (a)
x a
and the limit exists. Show that lim
x!a
f (x) = f (a) . So,
f (x) f (a) = (x a)
f (x) f (a)
x a
lim
x!a
[f (x) f (a)] = lim
x!a
(x a)
f (x) f (a)
x a
= lim
x!a
(x a) lim
x!a
f (x) f (a)
x a
= lim
x!a
(x a) f 0
(a)
= 0 f 0
(a) = 0
lim
x!a
f (x) = f (a)
VillaRINO DoMath, FSMT-UPSI
(D2) The Derivatives 21 / 21