1) The document is a lecture on real-valued functions that introduces concepts like domain and range, monotonic and strictly increasing/decreasing functions, algebra of functions including addition, multiplication, composition, and inverses, even and odd functions, and transformations of functions including reflection and shifting. 2) Key learning outcomes are determining limits of functions, computing limits, determining continuity, and understanding the relationship between limits and continuity. 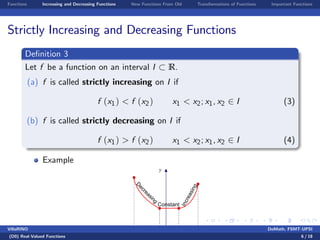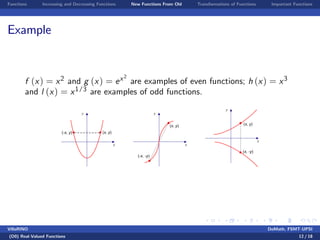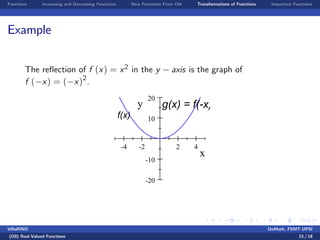3) Examples are provided to illustrate monotonic functions, function compositions, reflections, and shifts.

1. Beginning Calculus
-Real-Valued Functions -
Shahrizal Shamsuddin Norashiqin Mohd Idrus
Department of Mathematics,
FSMT - UPSI
(LECTURE SLIDES SERIES)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 1 / 18

2. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Learning Outcomes
Determine the existence of limits of functions
Compute the limits of functions
Determine the continuity of functions.
Connect the idea of limits and continuity of functions.
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 2 / 18

3. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Functions
De…nition 1
Let X and Y be any two nonempty sets. A function f from X to Y is a
rule that assigns each element x 2 X to a unique element y 2 Y .
f : X ! Y
f (x) = y, x 2 X, y 2 Y
x y
X Y
f
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 3 / 18

4. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Domain and Range
f (x) = y, x 2 X, y 2 Y
Remark 1
x 2 X is called the independent variable, and y 2 Y is the
dependent variable.
The set X is called the domain of f . The set Y is called the
codomain of f .
The range of f is the set fy 2 Y j y = f (x) , for some x 2 Xg .
The graph of f = f(x, f (x) j x 2 X)g
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 4 / 18

5. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Monotonic Functions
De…nition 2
Let f be a function on an interval I R
(a) f is called monotonic increasing (nondecreasing) on I if
f (x1) f (x2) x1 < x2; x1, x2 2 I (1)
(b) f is called monotonic decreasing (nonincreasing) on I if
f (x1) f (x2) x1 < x2; x1, x2 2 I (2)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 5 / 18

6. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Strictly Increasing and Decreasing Functions
De…nition 3
Let f be a function on an interval I R.
(a) f is called strictly increasing on I if
f (x1) < f (x2) x1 < x2; x1, x2 2 I (3)
(b) f is called strictly decreasing on I if
f (x1) > f (x2) x1 < x2; x1, x2 2 I (4)
Example
y
x-1-5 2 5
D
ecreasing
Increasing
Constant
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 6 / 18

7. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example
Each of the functions f , g, h in the table below is increasing, but each
increases in a di¤erent way. Match each function with its possible graph.
x f (x) g (x) h (t)
1 23 10 2.2
2 24 20 2.5
3 26 20 2.8
4 29 37 3.1
5 33 44 3.4
6 38 50 3.7
(a) (b) (c)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 7 / 18

8. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Algebra of Functions
De…nition 4
Given two functions f and g. De…ne f + g, f g, f g, and
f
g
as follows
(a) (f + g) (x) = f (x) + g (x) .
(b) (f g) (x) = f (x) g (x) .
(c) (f g) (x) = f (x) g (x) .
(d)
f
g
(x) =
f (x)
g (x)
, g (x) 6= 0.
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 8 / 18

9. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Composition of Functions
De…nition 5
Let f : X ! Y 0 and g : Y ! Z be functions. De…ne a new function
g f : X ! Z as follows:
(g f ) (x) = g (f (x)) , 8x 2 X (5)
The function g f is called the composition of f and g.
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 9 / 18

10. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Inverse of Functions
De…nition 6
Let f : X ! Y be a one-to-one correspondence function. Then f has
an inverse f 1 and,
f 1
(y) = x , y = f (x) x 2 X, y 2 Y (6)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 10 / 18

11. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Even and Odd Functions
De…nition 7
For any function f ,
(a) f is called an even function if f ( x) = f (x) , for all x in the
domain.
(b) f is called an odd function if f ( x) = f (x) , for all x in the
domain.
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 11 / 18

12. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example
f (x) = x2 and g (x) = ex2
are examples of even functions; h (x) = x3
and l (x) = x1/3 are examples of odd functions.
y
x
(-x, y) (x, y)
y
x
(-x, -y)
(x, y)
y
x
(x, -y)
(x, y)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 12 / 18

13. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Re‡ecting
De…nition 8
Let y = f (x). Then,
(a) the re‡ection of the graph of y = f (x) in the x axis is the graph
of y = f (x) .
(b) the re‡ection of the graph of y = f (x) in the y axis is the graph
of y = f ( x) .
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 13 / 18

14. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example
The re‡ection of f (x) = x2 in the x axis is the graph of
f (x) = x2.
-4 -2 2 4
-20
-10
10
20
x
y f(x)
g(x) = -f(x)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 14 / 18

15. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example
The re‡ection of f (x) = x2 in the y axis is the graph of
f ( x) = ( x)2
.
-4 -2 2 4
-20
-10
10
20
x
y g(x) = f(-x)
f(x)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 15 / 18

16. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Shifting
De…nition 9
Let c > 0 is any constant. Vertical and horizontal shifts in the graph of
y = f (x) are represented as follows:
(a) Vertical shift c units upward: g (x) = f (x) + c;
(b) Vertical shift c units downward: g (x) = f (x) c;
(c) Horizontal shift c units to the right: g (x) = f (x c)
(d) Horizontal shift c units to the left: g (x) = f (x + c)
VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 16 / 18

17. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example
Let f (x) = x3. Then the graph of a function:
g (x) = x3 + 3 = f (x) + 3 is obtained by shifting the graph of
f (x) = x3, 3 unit upward.
-4 -2 2 4
-4
-2
2
4
x
y
f(x)
g(x) = f(x)+3
g (x) = x3 3 = f (x) 3 is obtained by shifting the graph of
f (x) = x3, 3 unit downward.
4y f(x)VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 17 / 18

18. Functions Increasing and Decreasing Functions New Functions From Old Transformations of Functions Important Functions
Example - continue
g (x) = (x + 3)3
= f (x + 3) is obtained by shifting the graph of
f (x) = x3, 3 unit to the left..
-4 -2 2 4
-4
-2
2
4
x
y
f(x)
g(x) = f(x+3)
g (x) = (x 3)3
= f (x 3) is obtained by shifting the graph of
f (x) = x3, 3 unit to the right..
4y
f(x)VillaRINO DoMath, FSMT-UPSI
(D0) Real-Valued Functions 18 / 18