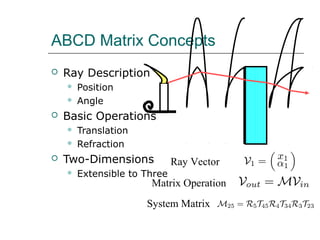
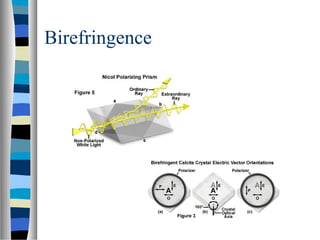
This document provides an overview of matrix concepts and their application to optics. It discusses: 1) How matrices can be used to represent optical systems and describe the propagation of light rays through multiple components using basic operations like translation and refraction. 2) Common matrix representations for optical elements like lenses, mirrors, and polarization elements. The determinant of cascaded matrices can be used to describe properties of the overall optical system. 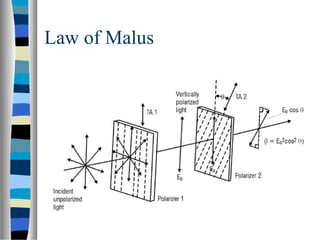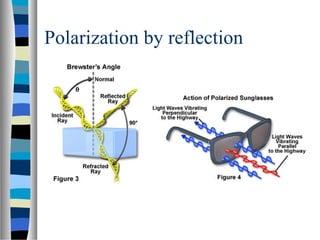3) How Jones matrices represent the change in polarization state of light passing through or reflecting off an optical element, allowing polarization effects to be analyzed.

1. ABCD Matrix Concepts
 Ray Description
 Position
 Angle
 Basic Operations
 Translation
 Refraction
 Two-Dimensions
 Extensible to Three
Ray Vector
Matrix Operation
System Matrix

2. Cascading Matrices








⋅ℑ=







'
1
'
12
2
2 1
νν
xx






⋅ℜ=







2
2
2'
2
'
2
νν
xx






⋅ℜ=







1
1
1'
1
'
1
νν
xx
Generic Matrix:
Determinant (You can show that
this is true for cascaded matrices)
V1 R1 T12 R2 V’2
Light Travels Left to Right, but
Build Matrix from Right to Left
1






⋅ℜ⋅ℑ⋅ℜ=







1
1
1122'
2
'
2
νν
xx
112212 ℜ⋅ℑ⋅ℜ=Μ

3. Matrices for Optical Components
 Free space
 Refraction at a planar
boundary
 Refraction at a spherical
boundary
 Transmission through thin
lens
 Reflection from a planar
mirror
 Reflection from a spherical
mirror








=ℑ
10
1
n
d
( )








−−=ℜ
1
01
12
R
nn








−=ℑ 1
1
01
f






=ℜ
10
01








=ℜ
1
2
01
R






=ℜ
10
01

4. Properties of a system from its matrix
 If D = 0, all rays entering the input plane
from the same point emerge at the
output plane making the same angle with
the axis. The input plane must be the
focal plane of the system
 If B = 0, all rays leaving the point O at
the input will pass through the same point
I at the output. This is the condition for
object-image relationship to occur. In
addition, A or 1/D will give the transverse
magnification produced by the system

5. Properties of a system from its matrix
 If C = 0, all rays which enter the system
parallel to one another will emerge
parallel to one another in a new direction.
This is a telescopic system.
 If A = 0, all rays entering the system at
the same angle will pass through the
same point in the output plane. The
system brings a bundle of parallel rays to
a focus at the output plane.

6. Matrix representing polarization
A monochromatic plane wave of frequency f traveling
in the z direction is completely characterized by the
complex envelopes Exo=ax exp (jδx) and Eyo=ay exp (jδy)
of the x and y component of the electric field. It is
convenient to write these complex quantities in the
form of a column matrix,








=








=





= δδ
δ
j
y
x
j
y
j
x
yo
xo
ea
a
ea
ea
E
E
J y
x
Jones vector
Where δ = δy - δx

7. Matrix representing polarization –
degenerate state
Linearly polarized wave in x
direction
Linearly polarized wave, plane
of polarization making angle θ
with x axis
Left circularly polarized
Right circular polarized




0
1




θ
θ
sin
cos




j
1
2
1






− j
1
2
1

8. Optical Element Jones Matrix
linear horizontal polarizer
linear vertical polarizer
linear polarizer at
linear polarizer at -45°
quarter-wave plate, fast axis vertical
quarter-wave plate, fast axis horizontal
circular polarizer, right-handed
circular polarizer, left-handed
Matrix representing polarization –
polarizing element

9. Matrix Representation of
Polarization Devices
Consider the transmission of a plane wave of
arbitrary polarization through an optical system that
maintains the plane wave nature of the wave, but
alters its polarization
The system is assumed to be linear, so that the
principle of superposition of optical fields is obeyed.
The complex envelopes of two electric –field
components of the input (incident) wave, E1x and E1y
and those of the output (transmitted or reflected )
wave , E2x and E2y, are in general related by the
weighted superpositions
E2x = T11E1x+T12E1y
E2y= T21E1x+T22E1y,

10. Matrix Representation of
Polarization Devices
Where T11, T12, T21 and T22 are constants describing the
device. The above equation are general relations that
all linear optical polarization devices must satisfy.
The linear relations in above equations may
conveniently be written in matrix notation by defining
a 2 x 2 matrix T with element T11, T12, T21, and T22 so
that






=





2221
1211
2
2
TT
TT
E
E
y
x






y
x
E
E
1
1 The matrix T, called the Jones
matrix, describes the optical
system, whereas the vectors J1
and J2 describe the input and
output waves.J2 = TJ1

11. Optical Material
Anisotropic Material: A dielectric medium is
said to be anisotropic if its macroscopic
optical properties depends on direction.
The macroscopic properties of matter are of
course governed by the microscope
properties: The shape and orientation of
the individual molecules and the
organization of the molecules in space.

12. Optical material – continued..
The following is description of the positional and
orientational types of order inherent in several kinds
of optical materials .
– If the molecules are located in space at totally random
position and are themselves is isotropic or are oriented
along totally random direction , the medium is isotropic.
Gases, liquids, and amorphous solid are isotopic.
– If the molecule and the orientation are not totally random,
the medium is anisotropic, even if the position are totally
random. This is the case for liquid crystals, which have
orientation order but lack complete positional order.

13. Optical material – continued..
– If the molecules are organized in space according
to the regular periodic pattern and are oriented in
same direction, as in crystal, the medium is in
general anisotropic.
– Polycrystalline materials have a structure in the
form of disjoined crystalline grains that are
randomly oriented relative to the each other. The
grains are themselves generally anisotropic, but
their average macroscopic behavior is isotropic.

14. Optical material – continued…
Polaroid Material
– Polaroid is the trade name for the most commonly
used dichroic material.
– It selectively absorbs light from one plane, typically
transmitting less than 1% through a sheet of
polaroid. It may transmit more than 80% of light in
the perpendicular plane.
– Polaroid materials accomplish polarization by
dichroism. At angles other than 90°, the
transmitted intensity is given by the Law of Malus.

15. Optical material – continued..
Dichroism
– Causes visible light to split into distinct
beams of different wavelengths, or
– One in which light rays having different
polarizations are absorbed by different
amount
There is a distinct difference between
dichroism and dispersion

16. Law of Malus
When unpolarized light passes through a polarizer,
the light intensity—proportional to the square of its
electric field strength—is reduced, since only the E-
field component along the transmission axis of the
polarizer is passed.
When linearly polarized light is directed through a
polarizer and the direction of the E-field is at an angle
θ to the transmission axis of the polarizer, the light
intensity is likewise reduced. The reduction in
intensity is expressed by the law of Malus, I=I0cos2
θ

17. Law of Malus

18. Polarization by reflection
Unpolarized light can also undergo polarization by
reflection off nonmetallic surfaces. The extent to
which polarization occurs is dependent upon the
angle at which the light approaches the surface and
upon the material which the surface is made of.
A person viewing objects by means of light reflected
off nonmetallic surfaces will often perceive a glare if
the extent of polarization is large.
Metallic surfaces reflect light with a variety of
vibrational directions; such reflected light is
unpolarized.

19. •For normal incidence case, the reflection
coefficient and transmission coefficient is
independent of polarization, because the
electric and magnetic fields are both always
tangential to the boundary
•This is not the case for wave with an
oblique angle, because the polarization is
not always tangential to the surface or
boundary
Polarization by reflection

20. Polarization by reflection
Brewster’s angle is an angle of incidence at which
light with a particular polarization is perfectly
transmitted through a transparent nonmetalic
surfaces.
θB = arctan (n2/n1)
The angle of reflection and angle of refraction adds
up to be 90o
Light that reflects from a surface at this angle is
entirely polarized perpendicular to the incident plane -
GLARE
If the angle is not exactly Brewster’s angle the
reflected ray will only be partially polarized

21. Polarization by reflection

22. Glare from water surface Glare blocked by vertical polarizer
Polarization by reflection

23. There are two types of polarization relative to the plane
of incidence
1. Parallel polarization
(TM polarization)
2. Perpendicular polarization
(TE polarization)
Plane of polarization is defined by the plane containing
the normal of the boundary and the direction of
propagation of the incident wave.
Relative to E
Polarization by reflection

24. Polarization by reflection

25. Perpendicular polarization
The reflection and transmission coefficients are given by
θηθη
θηθη
coscos
coscos
12
12
+
−
==Γ
⊥
⊥
⊥
i
ti
i
o
r
o
E
E
ti
i
i
o
t
o
E
E
θηθη
θη
τ
coscos
cos2
12
2
+
==
⊥
⊥
⊥
1+Γ= ⊥⊥τ

26. it
it
i
o
r
o
E
E
θηθη
θηθη
coscos
coscos
12
12
||
||
||
+
−
==Γ
it
i
i
o
t
o
E
E
θηθη
θη
τ
coscos
cos2
12
2
||
||
||
+
==
Parallel polarization
The Fresnel reflection and transmission coefficients are
given by
1|||| +Γ=τ

27. Polarization by refraction
•Polarization can also occur by
the refraction of light. Refraction
occurs when a beam of light
passes from one material into
another material.
•At the surface of the two
materials, the path of the beam
changes its direction. The
refracted beam acquires some
degree of polarization

28. Birefringence
Birefringence, or double refraction, is the division
of a ray of light into two rays (the ordinary ray and the
extraordinary ray) when it passes through certain
types of material, such as calcite crystals, depending
on the polarization of the light.
This is explained by assigning two different
refractive indices to the material for different
polarizations. The birefringence is quantified by:
Δn = ne - no
where no is the refractive index for the ordinary ray and ne is the
refractive index for the extraordinary ray.

29. Birefringence
When a beam of ordinary unpolarized light is incident
on a calcite or quartz crystal, there will be, in addition
to the reflected beam, two refracted beams in place
of the usual single one observed, e.g., in glass.
This phenomenon is called double refraction or
birefringence.
Upon measuring the angles of refraction for different
angles of incidence, one finds that Snell's law of
refraction holds for one ray but not for the other. The
ray for which the law holds is called the ordinary ray
and the other is called the extraordinary ray.

30. Birefringence
Unpolarized light entering a birefringent
crystal is split into two linearly polarized
beams which are refracted by different
amounts.
There are two refractive indices
Optic axis: this is the direction within the crystal along which
there is no double refraction.

31. Birefringence

32. Application of polarization
Linear polarizar
– The linear polarizer selectively removes all
or most of the E fields in a given direction,
while allowing fields in the perpendicular
direction to be transmitted.
– In most cases, the selectivity is not 100%
efficient, so the transmitted light is partially
polarized

33. Application of polarization
Phase retarder
– The phase retarder does not remove either
of the component orthogonal E fields but
introduces a phase difference between
them.
– If light corresponding to each vibration
travels with different speeds through such
a retardation plate, there will be cumulative
phase difference between the two waves

34. Application of polarization
Rotator
– The rotator has the effect of rotating the
direction of linearly polarized light incident
on it by some particular angle.
– The effect of the rotator element is to
transmit linearly polarized light whose
direction of vibration has rotated
counterclockwise or vice versa, by an
angle θ