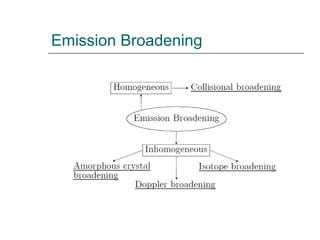
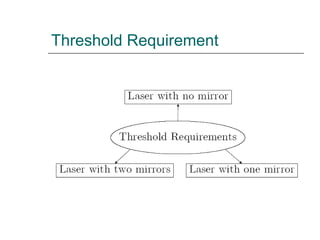
The document discusses key concepts related to laser emission and operation, including: 1. Stimulated emission cross section is a constant that determines the relationship between gain and stored energy in a laser medium. It depends on emission wavelength. 2. Homogeneous and inhomogeneous broadening contribute to the linewidth of laser emission. 3. Threshold requirements refer to the gain needed for a laser beam to reach saturation intensity after passing through an amplifier multiple times with mirrors. 4. Resonator stability depends on mirror curvature, with stable resonators keeping light near the axis and unstable resonators producing doughnut-shaped output beams. 5. Pumping techniques include direct, optical, and particle pumping to excite the

1. Emission Broadening

2. Emission Cross Section
Definition: material parameters for quantifying the likelihood or rate
of optical transition event
Stimulated Emission Cross Section
 It is a constant for a specific laser transition in a specific gain
medium
 It is strongly dependent on the emission wavelength
 Is essential for calculations of the expected performance because
it determines the relationship between the gain and the energy
stored
Homogeneous Broadening
æ
1
( ) ÷ ÷ø
H
ul n
s n 2
Inhomogeneous Broadening
ö
ç çè
= ul ul
H
D
o
A
n
l
p
2
4 2
ö
1/ 2 2 ln 2
æ
1
= æ D
ö çè
( ) ÷ ÷ø
ç çè
D
D
ul n
s n 2
÷ø
ul ul
o
A
n
l
p p
4
Linewidth of emission

3. Threshold Requirement
Definition
 The necessary requirements for the beam to grow to
the point at which it reaches the saturation intensity Isat
 The saturation intensity, Isat is arbitrarily defined as the
intensity at which the stimulated rate downward equals
the normal radiative decay rate,
I c
ul ( ) u
sat B n
n t
=

4. Threshold Requirement

5. Threshold Requirement
Laser With No Mirror
 The beam would meet the threshold gain requirement if,
= ( )D @ 12 ± 5 th sat ul ul sat g L s n N L
 This is to ensure that the beam can develop a well defined
direction before Isat is reached
 It is shown that,
2
ö
æ
e th sat L
16 ÷ ÷ø
ç çè
g L sat
=
a
d
Diameter of amplifier
Threshold gain
Laser beam divergence

6. Threshold Requirement
Laser With One Mirror
 Adding a mirror can be thought of as adding a second
amplifier
 Assuming that the beam just reaches Isat after two passes
through the amplifier, the gain medium would meet the
threshold gain requirement if,
g L = g (2L) = g L = ( )DN (2L) @ 12 ± 5 th sat th th eff ul ul s n
oThe beam is narrower, as it emerges from the end of the
amplifier

7. Threshold Requirement
Laser With Two Mirrors
 Placing a mirror at each end of the amplifier effectively
adds an infinite series of amplifiers behind the original
amplifier
 A slight amount of light is allowed to leak out the end
by using a mirror with 99.9% reflectivity
 Two factors determine if a two-mirror laser can reach Isat
1. Net gain per trip
2. Sufficient gain duration
 The beam emerges with a very narrow angular
divergence

8. Threshold Requirement
Net Gain per Round Trip
 The minimum round-trip steady-state
requirement for the threshold of lasing is
that the gain exactly equal the loss,
The solution for the threshold gain is then,

9. Resonator Stability

10. Resonator Stability
Stable Resonators
 The curvatures of the mirrors keep the light
concentrated near the axis of the resonator
 The only way light can escape from the resonator
is to go through one of the mirrors

11. Resonator Stability
Unstable Resonators
 The light rays continue to move away resonator axis
until eventually they miss convex mirror altogether
 The output beam from this resonator doughnut-like
shape with a hole in the middle
 The advantage is that they usually produce larger
beam volume inside the gain medium

12. Pumping Techniques

13. Pumping Techniques
Direct Pumping
 The excitation flux is sent directly to the upper laser
level u from a source or target state j, in which the
source state is the highly populated ground state 0
of the laser species

14. Pumping Techniques
Optical Pumping
 Often used for solid-state and
organic dye lasers
Particle Pumping
 Generally used for gas lasers and
also semiconductor lasers

15. Pumping Techniques
Direct Pumping
Disadvantages
 Several effects can prevent direct pumping from being an effective
excitation process for many potential lasers. These effects are listed
as follows.
 1. There may be no efficient direct route from the ground state 0 to
the laser state u. For optical pumping, that would mean that the B0u
associated with pump absorption is too small to produce enough gain;
for particle pumping, it would mean that the electron collisional
excitation cross section σ0u is too small.
 2. There may be a good direct route from 0 to u, but there may also
be a better route from 0 to l (the lower laser level) by the same
process. In this case Γ0l/Γ0u may be too large to allow an inversion.
 3. Even though there may be a good probability for excitation - via
absorption either of the pump light associated with B0u for optical
excitation or of σ0u
e for electron excitation - there may not be a good
source of pumping flux available. That is, there may be insufficient
intensity, I for optical pumping, or insufficient density Np (or electron
density ne) for particle pumping, at the specific energies necessary for
pumping population from level 0 to level u.

16. Pumping Techniques
Indirect Pumping
 Indirect pumping processes all involve an intermediate level
q and can be considered in three general categories as
diagrammed in the figure below: transfer from below,
transfer across, and transfer from above.

17. Cavity Modes
Longitudinal Laser Cavity Modes
 We have seen that one or more longitudinal laser mode
frequencies can occur when a two-mirror cavity is placed
around the laser gain medium and sufficient time
(typically 10 ns to 1 μs) is allowed for such modes to
develop. The total number of modes present is determined
by the separation d between the mirrors, as well as by the
laser bandwidth and type of broadening (homogeneous or
inhomogeneous) that is present. The actual laser mode
frequencies can be obtained by,
m c
2
ö çè
÷ø
= æ
nd
n
for lasers in which the index of refraction n is the same
throughout the pathway of the laser beam within the optical
cavity, as shown in the figure on the next slide.
Remember that m is a positive integer so as to satisfy the
standing-wave conditions of the Fabry-Perot resonator.

18. Cavity Modes
Longitudinal Laser Cavity Modes
 This expression is valid for almost all gas lasers, as well as
for solid-state and dye lasers in which the mirrors are
placed immediately at the ends of the gain medium. If a
laser has a space of length d - L between the gain medium
and the mirrors, and if that cavity space has a different
value for the index of refraction nc than the index nL of the
laser gain medium, then a specific laser mode frequency
associated with a mode number m can be expressed as,
ö
ù
1
[ ] ÷ ÷ø
æ
ç çè
úû
é
êë
- +
=
n d L n L
m c
c L
2
n