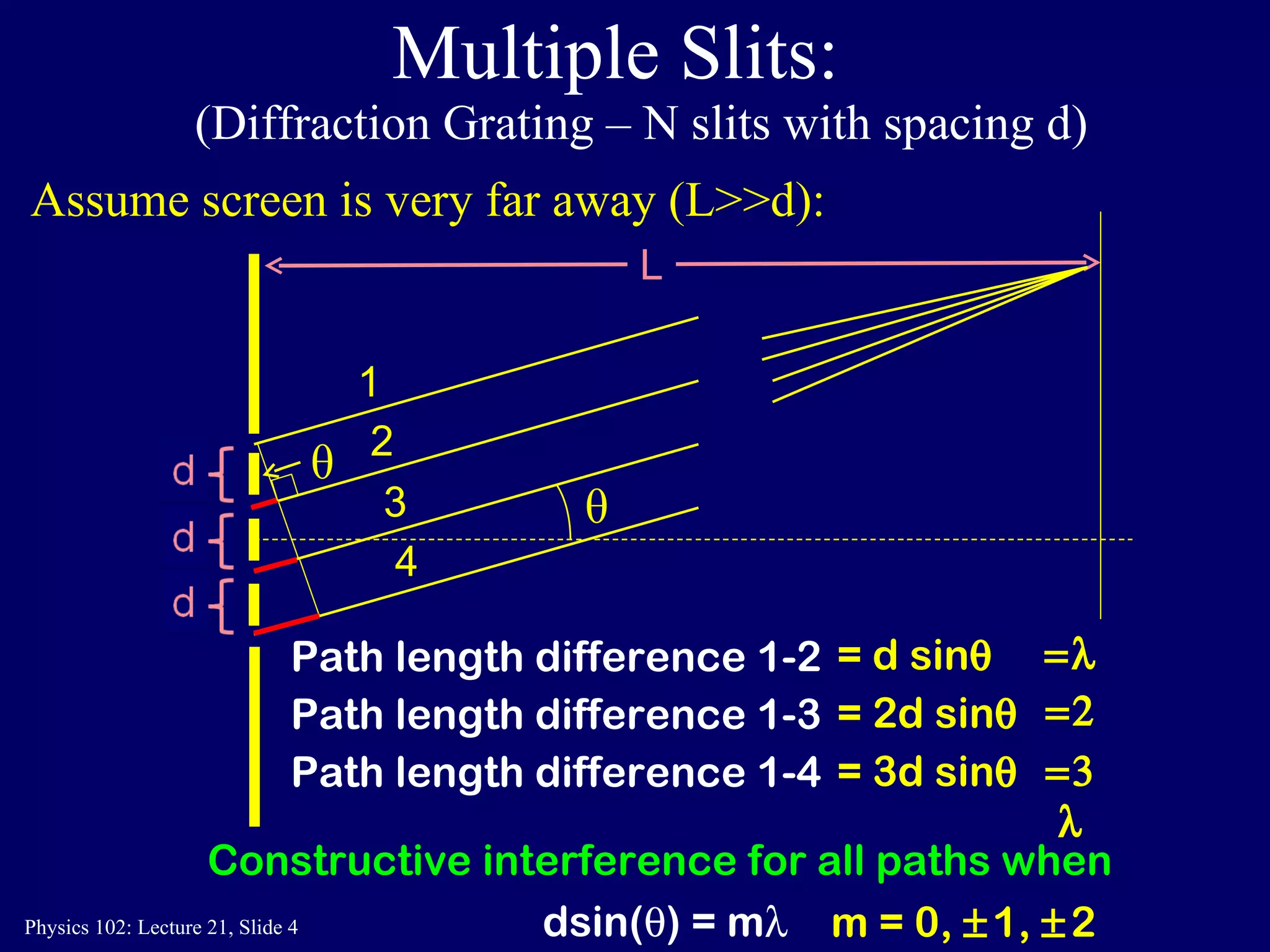
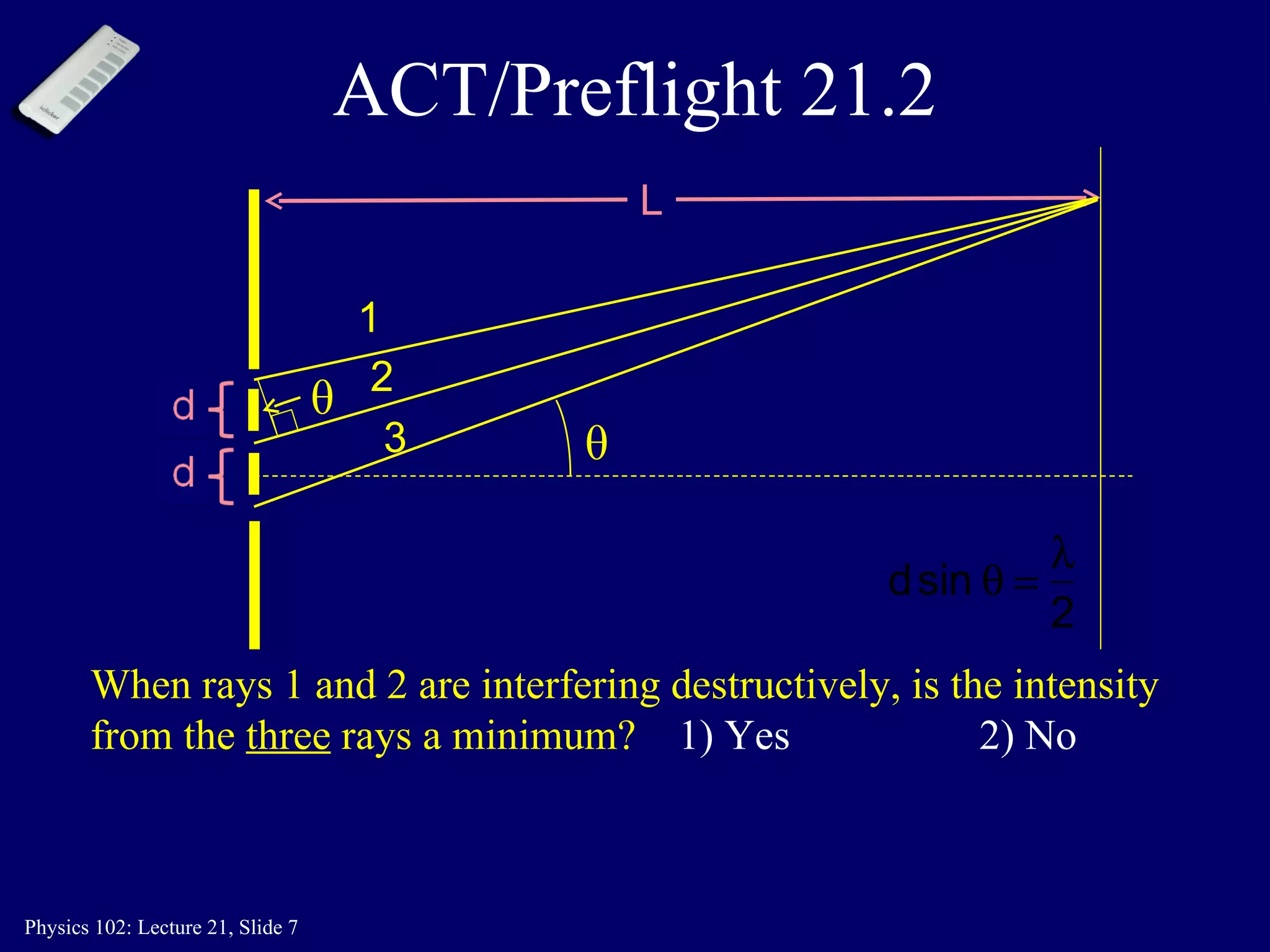
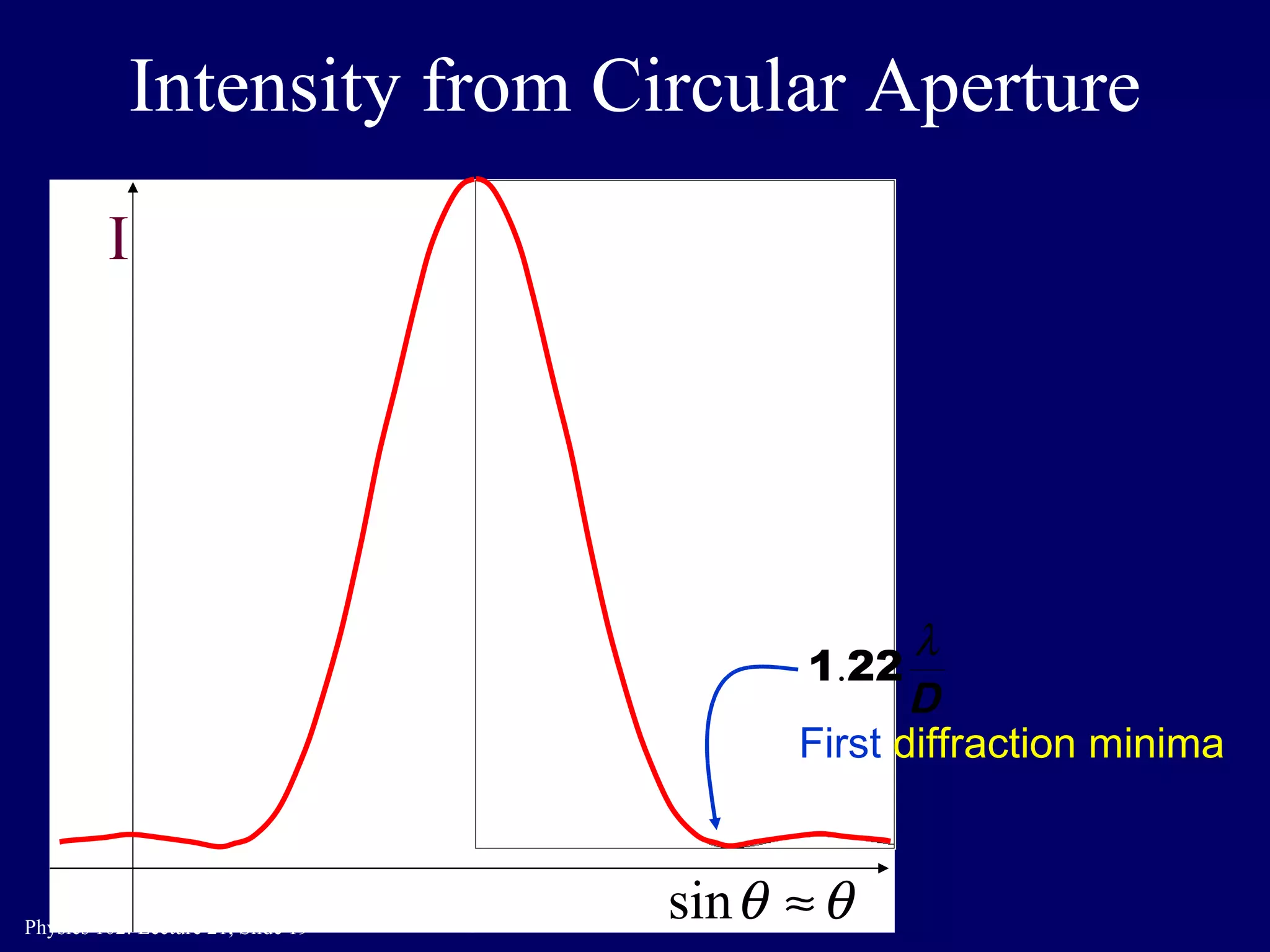
The document discusses various optical phenomena related to diffraction and interference of light, including: 1) Light passing through multiple slits will produce constructive interference when the path length difference is an integer multiple of the wavelength. 2) Single slit diffraction causes a diffraction pattern on a screen with alternating bright and dark bands. The location of the minima is determined by the slit width and wavelength. 3) Increasing the number of slits or decreasing the slit spacing results in narrower, brighter diffraction maxima.

1. Diffraction, Gratings, Resolving Power Physics 102: Lecture 21

2. Recall Interference (at least 2 coherent waves) Constructive (full wavelength difference) Destructive (half wavelength difference) Light (1 source, but different paths) Young’s double slit Thin films Multiple slit X-ray diffraction from crystal Diffraction/single slit Last lecture Today’s lecture

3. ACT: Double slit review θ L Which condition gives destructive interference? 1) dsin(  ) = m  2) dsin(  ) = (m+1/2)  m = 0,  1,  2 dsin(  ) θ y

4. Multiple Slits: (Diffraction Grating – N slits with spacing d) θ L Assume screen is very far away (L>>d): Path length difference 1-2 = d sin  Path length difference 1-3 = 2d sin  Path length difference 1-4 = 3d sin     Constructive interference for all paths when dsin(  ) = m  m = 0,  1,  2 θ 1 2 3 4

5. Multiple Slits: (Diffraction Grating – N slits with spacing d) θ L Assume screen is very far away (L>>d): m = 0,  1,  2 Holds for arbitrary N Constructive: dsin(  ) = m  Same condition as Young’s double slit! θ 1 2 3 4

6. θ L Preflight 21.1 All 3 rays are interfering constructively at the point shown. If the intensity from ray 1 is I 0 , what is the combined intensity of all 3 rays? 1) I 0 2) 3 I 0 3) 9 I 0 θ 1 2 3

7. θ L ACT/Preflight 21.2 When rays 1 and 2 are interfering destructively, is the intensity from the three rays a minimum? 1) Yes 2) No θ 1 2 3

8. Three slit interference I 0 9I 0

9. Multiple Slit Interference (Diffraction Grating) Region between maxima gets suppressed more and more as no. of slits increases – bright fringes become narrower and brighter. Peak location depends on wavelength! For many slits, maxima are still at 10 slits (N=10) intensity   0 2 slits (N=2) intensity   0

10. X-Ray Diffraction: A technique to study crystal structure 1 st maximum will be at 10 0 Crystal solid such as sodium Measure  , determine d Constructive interference: in NaCl For  =0.017nm X-ray d θ θ

11. Single slit interference? Monochromatic light travels through a screen with opening This is not what is actually seen! Bright spot Shadow

12. Diffraction/Huygens’ principle Huygens: Every point on a wave front acts as a source of tiny wavelets that move forward. Light waves originating at different points within opening travel different distances to wall, and can interfere! We will see maxima and minima on the wall! • • • • •

13. 1 st minima Central maximum

14. Single Slit Diffraction W Rays 2 and 2  also start w/2 apart and have the same path length difference. 1 st minimum at sin  =  /w Under this condition, every ray originating in top half of slit interferes destructively with the corresponding ray originating in bottom half. 1 1  2 2  When rays 1 and 1  interfere destructively.

15. Single Slit Diffraction w Rays 2 and 2  also start w/4 apart and have the same path length difference. 2 nd minimum at sin  = 2  /w Under this condition, every ray originating in top quarter of slit interferes destructively with the corresponding ray originating in second quarter. 1 1  2 2  When rays 1 and 1  will interfere destructively .

16. Single Slit Diffraction Summary Condition for quarters of slit to destructively interfere Condition for halves of slit to destructively interfere Condition for sixths of slit to destructively interfere THIS FORMULA LOCATES MINIMA !! Narrower slit => broader pattern All together… Note: interference only occurs when w >  (m =  1,  2,  3, …)

17. ACTS/Preflights 21.4, 21.5 A laser is shined onto a screen through a very small hole. If you make the hole even smaller, the spot on the screen will get: (1) Larger (2) Smaller Which drawing correctly depicts the pattern of light on the screen? (1) (2) (3) (4)

18. Diffraction from Circular Aperture Maxima and minima will be a series of bright and dark rings on screen Central maximum First diffraction minimum is at 1 st diffraction minimum  Diameter D light

19. Intensity from Circular Aperture I First diffraction minima

20. These objects are just resolved Two objects are just resolved when the maximum of one is at the minimum of the other.

21. Resolving Power To see two objects distinctly, need  objects >  min  min  objects Improve resolution by increasing  objects or decreasing  min  objects is angle between objects and aperture:  objects ≈ tan (d/y) sin  min ≈  min = 1.22  /D  min is minimum angular separation that aperture can resolve: D d y

22. ACT: Resolving Power How does the maximum resolving power of your eye change when the brightness of the room is decreased. 1) Increases 2) Constant 3) Decreases

23. Recap Interference: Coherent waves Full wavelength difference = Constructive ½ wavelength difference = Destructive Multiple Slits Constructive d sin(  ) = m  m=1,2,3…) Destructive d sin(  ) = (m + 1/2)  2 slit only More slits = brighter max, darker mins Single Slit: Destructive: w sin(  ) = m  m=1,2,3…)  Resolution: Max from 1 at Min from 2 opposite!