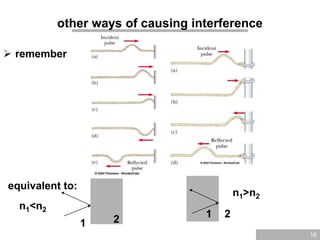
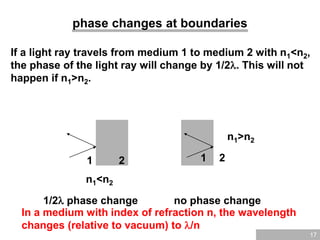
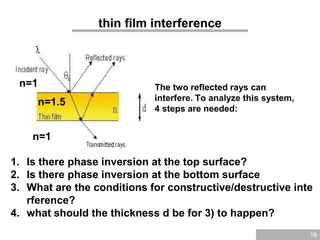
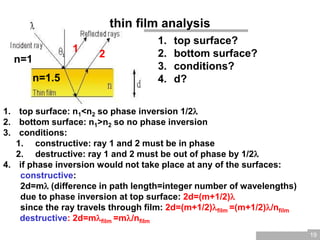
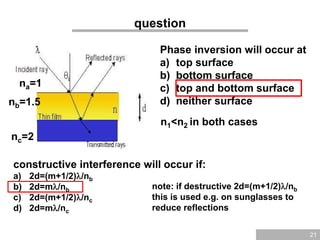
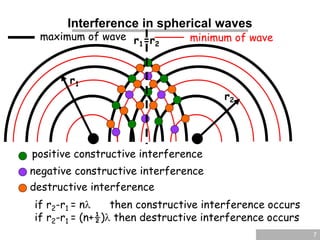
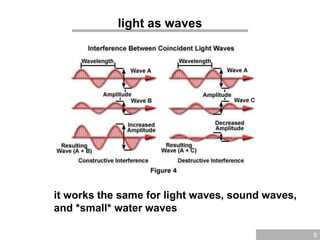
The document discusses wave optics, focusing on the wave nature of light and its phenomena such as interference, diffraction, and polarization. It explains concepts like coherence, monochromatic light, and the conditions for constructive and destructive interference, illustrated through Young's interference experiment and thin film interference. Additionally, it explores mathematical relationships governing these phenomena and presents questions to reinforce understanding.

1. WAVE OPTICS-I
Light has a dual nature and there are basic t
hree important phenomena which can be ex
plained if light is considered to have a wave
nature, e.g.
1. Interference
2. Polarization
3. Diffraction
1

2. INTERFERENCE

3. 3
light as waves
 so far, light has been treated as if it travels in straight lines
ray diagrams
refraction, reflection
 To describe many optical phenomena, we have to treat ligh
t as waves.
 Just like waves in water, or sound
waves, light waves can interact
and form interference patterns.
Remember c = f 

4. Interference
Coherence and Monochromatic
 No coherence between two light bulbs
Coherence time
Coherence length
Some later time or distance
coherence - two or more waves
that maintain a constant phase re
lation.
monochromatic - a wave that is c
omposed of a single frequency. H
eisenberg uncertainty relation.

5. 5
interference
constructive interference destructive interference
at any point in time one can construct the total amplitude
by adding the individual components

6. 6
Interference III
constructive interference
waves in phase
demo: interference
+
=
destructive interference
waves ½ out of phase
+
=





7. 7
Interference in spherical waves
maximum of wave minimum of wave
positive constructive interference
negative constructive interference
destructive interference
if r2-r1 = n then constructive interference occurs
if r2-r1 = (n+½) then destructive interference occurs
r1
r2
r1=r2

8. 8

9. 9
light as waves
it works the same for light waves, sound waves,
and *small* water waves

10. 10
double slit experiment
•the light from the two so
urces is incoherent (fi
xed phase with respect t
o each other
•in this case, there is
no phase shift between
the two sources
•the two sources of light
must have identical wave
lengths

11. 11
Young’s interference experiment
there is a path difference: depending on its size the waves
coming from S1 or S2 are in or out of phase

12. 12
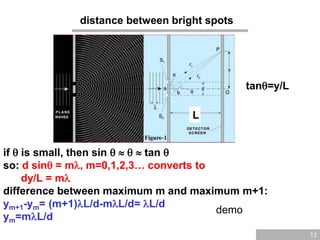
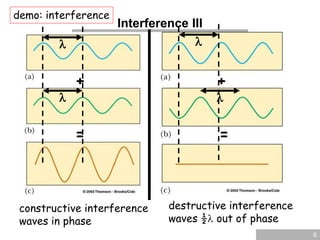
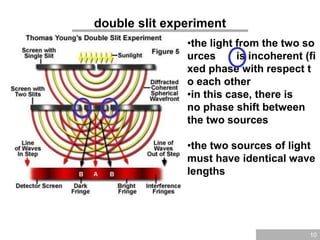
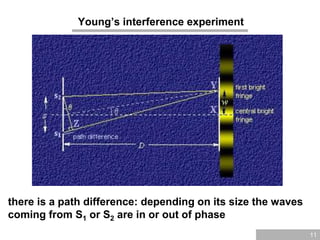
Young’s interference experiment
If the difference in distance between the scr
een and each of the two slits is such that th
e waves are in phase, constructive interfere
nce occurs: bright spot difference in distan
ce must be a integer multiple of the wavele
ngth:
d sin = m, m=0,1,2,3…
m = 0: zeroth order, m=1: first order, etc.
if the difference in distance is off by half a
wavelength (or one and a half etc.),
destructive interference occurs
(d sin = [m+1/2], m=0,1,2,3…)
path difference demo

13. 13
distance between bright spots
if  is small, then sin     tan 
so: d sin = m, m=0,1,2,3… converts to
dy/L = m
difference between maximum m and maximum m+1:
ym+1-ym= (m+1)L/d-mL/d= L/d
ym=mL/d
tan=y/L
L
demo

14. 14
question
 two light sources are put at a distance d from a screen. Eac
h source produces light of the same wavelength, but the so
urces are out of phase by half a wavelength. On the screen
exactly midway between the two sources … will occur
 a) constructive interference
 b) destructive interference
+1/2
distance is equal
so 1/2 difference:
destructive int.

15. 15
question
 two narrow slits are illuminated by a laser with a wavelength of 600 nm.
the distance between the two slits is 1 cm. a) At what angle from the be
am axis does the 3rd order maximum occur? b) If a screen is put 5 mete
r away from the slits, what is the distance between the 0th order and 3rd
order maximum?
a) use d sin = m with m=3
=sin-1(m/d)=sin-1(3x600x10-9/0.01)=0.01030
b) Ym = mL/d
m=0: y0 =0
m=3: y3 = 3x600x10-9x5/0.01 = 9x10-4 m = 0.9 mm

16. 16
other ways of causing interference
 remember
equivalent to:
1 2
n1<n2
n1>n2
1 2

17. 17
phase changes at boundaries
If a light ray travels from medium 1 to medium 2 with n1<n2,
the phase of the light ray will change by 1/2. This will not
happen if n1>n2.
1 2
n1<n2
1/2 phase change
n1>n2
1 2
no phase change
In a medium with index of refraction n, the wavelength
changes (relative to vacuum) to /n

18. 18
thin film interference
n=1
n=1.5
n=1
The two reflected rays can
interfere. To analyze this system,
4 steps are needed:
1. Is there phase inversion at the top surface?
2. Is there phase inversion at the bottom surface
3. What are the conditions for constructive/destructive inte
rference?
4. what should the thickness d be for 3) to happen?

19. 19
n=1
n=1.5
n=1
thin film analysis
1. top surface?
2. bottom surface?
3. conditions?
4. d?
1. top surface: n1<n2 so phase inversion 1/2
2. bottom surface: n1>n2 so no phase inversion
3. conditions:
1. constructive: ray 1 and 2 must be in phase
2. destructive: ray 1 and 2 must be out of phase by 1/2
4. if phase inversion would not take place at any of the surfaces:
constructive:
2d=m (difference in path length=integer number of wavelengths)
due to phase inversion at top surface: 2d=(m+1/2)
since the ray travels through film: 2d=(m+1/2)film =(m+1/2)/nfilm
destructive: 2d=mfilm =m/nfilm
1
2

20. 20
Note
The interference is different for light of different
wavelengths

21. 21
question
na=1
nb=1.5
nc=2
Phase inversion will occur at
a) top surface
b) bottom surface
c) top and bottom surface
d) neither surface
n1<n2 in both cases
constructive interference will occur if:
a) 2d=(m+1/2)/nb
b) 2d=m/nb
c) 2d=(m+1/2)/nc
d) 2d=m/nc
note: if destructive 2d=(m+1/2)/nb
this is used e.g. on sunglasses to
reduce reflections

22. The End……
PHY232 - Remco Zegers - interference, diffraction & polarization 22