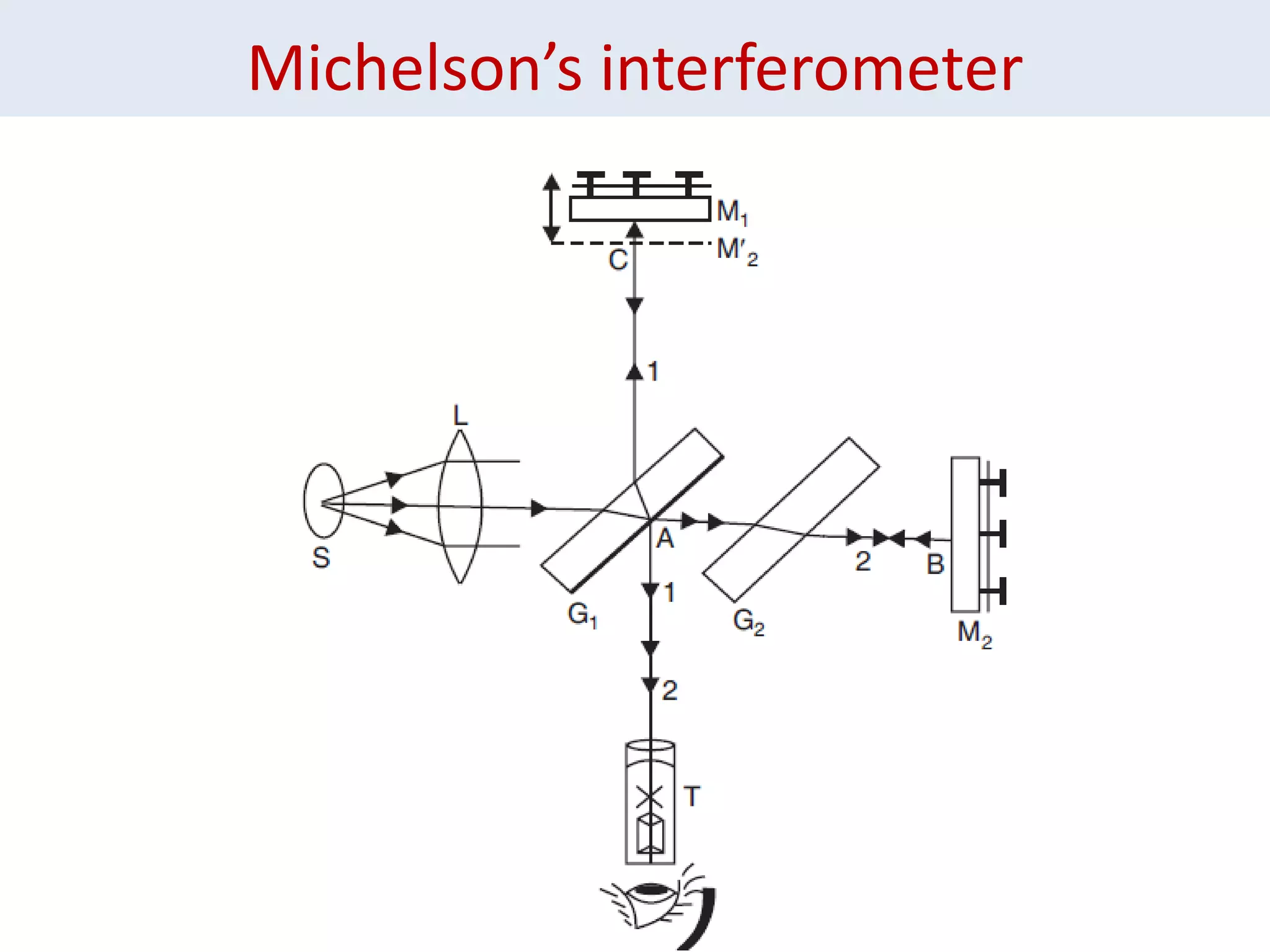
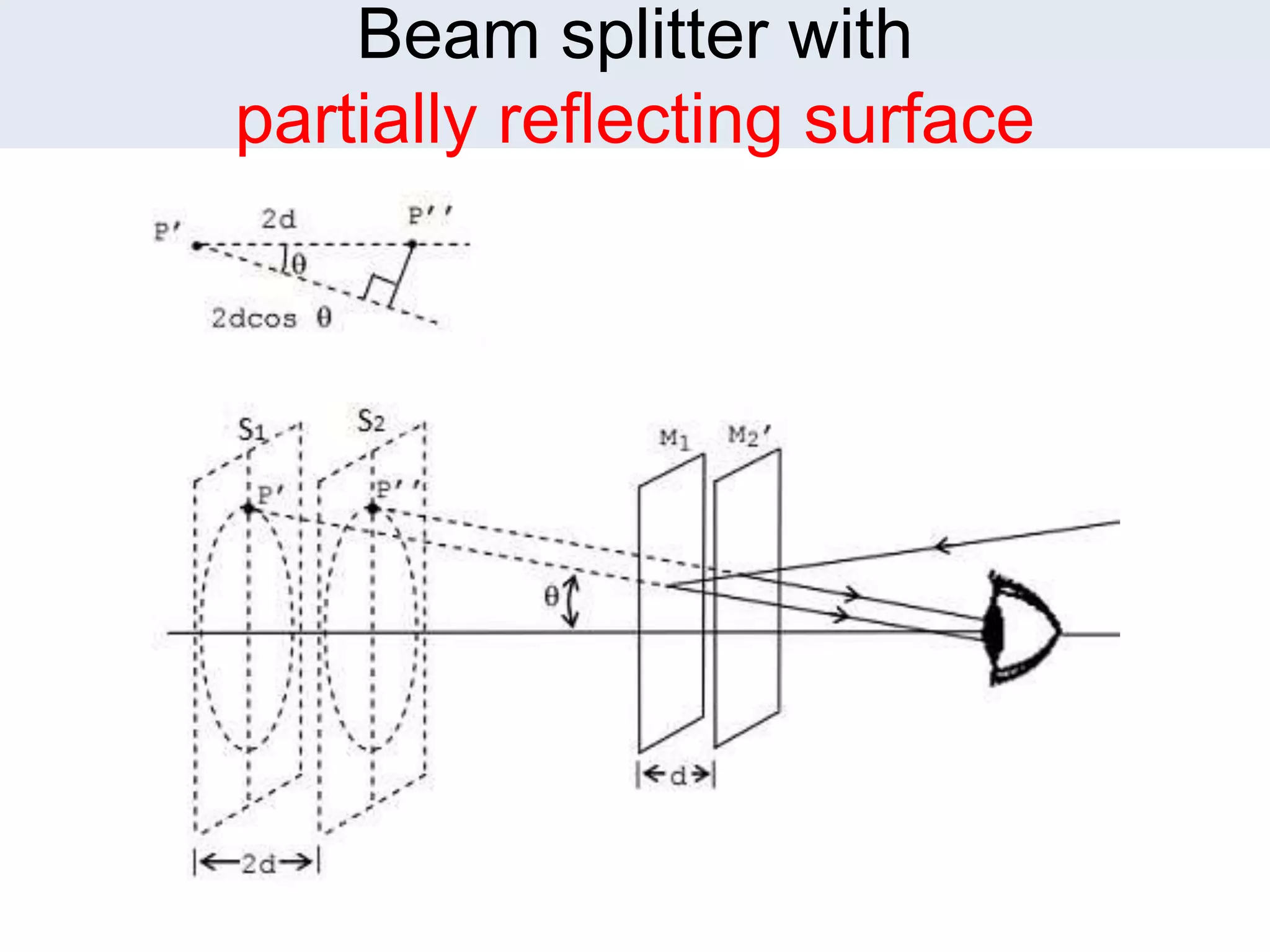
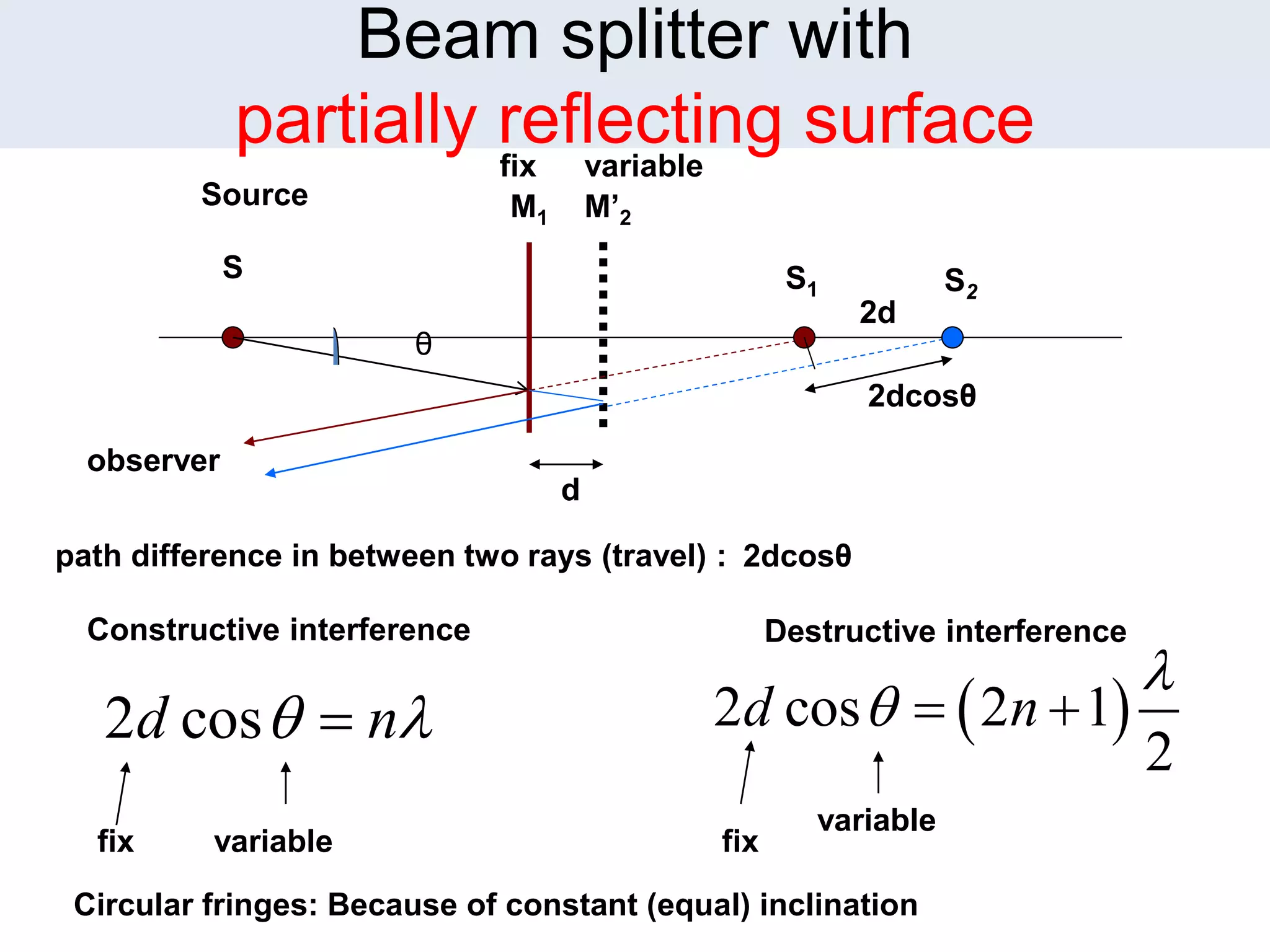
1. Michelson's interferometer uses a beam splitter to split light into two beams that travel different paths and are recombined, creating interference patterns of light and dark fringes. 2. The document discusses the conditions for constructive and destructive interference for Michelson's interferometer and how changing the orientation of the mirrors or using a glass plate as the beam splitter affects the interference patterns. 3. Methods for using Michelson's interferometer to determine properties are described, such as finding the wavelength of light, measuring differences in wavelengths, and determining the refractive index or thickness of transparent materials.

1. Applied Physics
Lecture – 4

2. Michelson’s interferometer

3. Beam splitter with
partially reflecting surface
Constructive interference:
Destructive interference =
2d n

 
2 2 1
2
d n

 

4. Beam splitter with
partially reflecting surface

5. M1
S S1
M’2
S2
d
2d
θ
2dcosθ
path difference in between two rays (travel) :
observer
fix variable
Circular fringes: Because of constant (equal) inclination
fix variable
Source
2 cos
d n
 

Beam splitter with
partially reflecting surface
2dcosθ
Constructive interference Destructive interference
 
2 cos 2 1
2
d n

  
fix
variable

6. Different orientation of the mirrors
When the two mirrors are tilted, the mirror M1 and the virtual
image M′2 are not parallel.
In this case the air path between them is wedge-shaped and the
fringes appear to be straight

7. Reflection and phase change
Reflected light will experience a 180 degree phase change when it
reflects from a medium of higher refractive index and no phase change
when it reflects from a medium of smaller refractive index

8. Beam splitter as Simple glass plate
Now, if the beam splitter is just a simple glass plate,
the beam reflected from mirror M2 will undergo an abrupt phase
change of  (when getting reflected by the beam splitter),
Constructive interference
Destructive interference
 
2 cos 2 1
2
d n

  
2 cos
d n
 


9. Beam splitter as Simple glass plate
Constructive interference when  = 0:
Destructive interference when  = 0
2d n

 
2 2 1
2
d n

 

10. 1. To find the wavelength of a given monochromatic
source of light
   
1 1
2 2
1 2 1 2
2
2
2
2
2
d m
d m
d d m m
x N
x
N







  



11. 2. Determination of the Difference in the Wavelength of
Two Waves
If a source of light consists of two wavelengths 1 and 2, which
differ slightly,
1 1 2 2
1 2 1 2
1 2
1 2 2
1 2 2
2
1 2
2d n n
If and n n, n n 1
2d n (n 1) (1)
n n
n( )
n (2)
( )
   
     
    
     
     


  
Where,
= wavelength
d = separation between two
position of distinctness
1 2
1 2
2
1 2
1 2
Substituting in eq 1
2d
2d 2d
 

  
  
     

12. 3. Determination of refractive index or
thickness of a plate
A transparent sheet of thickness t and refractive index  be
inserted in the path of one of the interfering beams.
The optical path of that beam increases because of the sheet.
It becomes ‘t’ instead of ‘t’.
Since the beam traverses the medium twice, the extra path
difference between the two interfering beams is
 
1
t t t
 
  
 
2 1
t 
 
If m is the number of fringes by which the fringe system is
displaced
 
 
2 1
2 1
t m
m
t
 


 



13. Diffraction
Diffraction of light is the phenomena bending of light around the
corners of an obstacle when the dimension of the obstacle is
comparable to the wavelength of the light

14. Diffraction

15. Difference between interference and
diffraction
Interference Diffraction
Produced from different
wave fronts.
Produced Different parts of
the same wave front
Good contrast between
maxima and minima
Poor contrast between
maxima and minima
width of the fringes may or
may not be equal
width of the fringes always
unequal
Intensity of bright fringes
equal
Intensity of bright fringes
unequal

16. Types of Diffraction
1. Fresnel diffraction:
The source of light or the screen or both at finite distances from
obstacle or aperture causing the diffraction.

17. Types of Diffraction
2. Fraunhofer diffraction
The source of light and the screen are effectively at infinite distances
from the obstacle or aperture which causes the diffraction
In practice, the arrangement for
Fraunhofer diffraction is achieved
by using two convergent lenses

18. Types of Diffraction
Our discussion is limited to Fraunhofer diffraction
In practice, the arrangement for Fraunhofer diffraction is
achieved by using two convergent lenses

19. Fraunhofer diffraction due to single slit
Em, Im

20. Fraunhofer diffraction due to single slit

21. Thank you