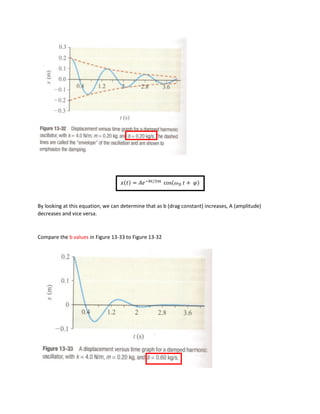
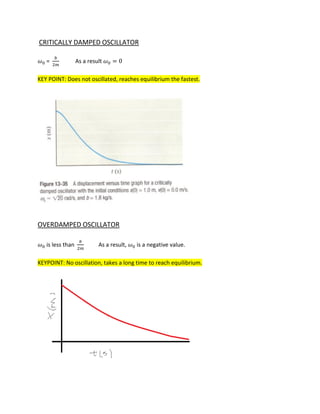
Damped oscillations are oscillations with drag force acting on the system, causing the amplitude to decrease exponentially over time. The oscillation frequency depends on the natural frequency, mass, and drag constant. In an underdamped oscillator, the natural frequency is greater than half the drag constant divided by the mass, resulting in a positive oscillation frequency and decreasing amplitude oscillations. Critically damped oscillators have a natural frequency equal to half the drag constant divided by the mass, reaching equilibrium without oscillations. Overdamped oscillators have a natural frequency less than half the drag constant divided by the mass, with no oscillations and a long time to reach equilibrium.

1. Damped Oscillation
Recall: Oscillation is “one complete back-and-forth motion”
Damped oscillations are oscillations with 𝐹𝐷 (drag force) acting on the system
Oscillation frequency:
𝜔 𝐷 = √
𝑘
𝑚
+ (
𝑏
2𝑚
)
2
𝜔 𝐷 = √ 𝜔0
2
+ (
𝑏
2𝑚
)
2
𝑤 𝐷 is oscillation frequency (Hz)
𝑤0 is natural frequency (Hz)
b is drag constant (kg/s)
m is mass (kg)
UNDERDAMPED OSCILLATOR
𝜔0 is greater than
𝑏
2𝑚
As a result, 𝑤 𝐷 is a positive value
KEY POINT: Amplitude decrease exponentially as time increases due to 𝐹𝐷!
𝑥(𝑡) = 𝐴(𝑡) cos(𝜔 𝐷 𝑡 + 𝜑)
where 𝐴(𝑡) = 𝐴𝑒−𝑏𝑡/2𝑚

2. 𝑥(𝑡) = 𝐴𝑒−𝑏𝑡/2𝑚
cos(𝜔 𝐷 𝑡 + 𝜑)
By looking at this equation, we can determine that as b (drag constant) increases, A (amplitude)
decreases and vice versa.
Compare the b values in Figure 13-33 to Figure 13-32

3. The b value in Figure 13-33 is greater than the b value in Figure 13-32.
Figure 13-33 with a greater b value has a smaller amplitude whereas Figure 13-32 with a smaller b value
has a greater amplitude.
This confirms that as b increases, A decreases.
QUESTION:
Which of the following graph has a greater b-value?
Answer: B
Rationale: The answer is definitely not D because D is not an exponentially decreasing graph.
This leaves A, B, and C.
Let’s examine A and C. As the drag constant increases, amplitude decreases, thus, A with
a greater amplitude is eliminated.
Now, only B and C remains.
At first glance, C may seem to be the correct answer; however, it is not. After carefully
examining the graph, it is shown that C has units in m and B has units in cm.
The smaller amplitude is seen in B.

4. CRITICALLY DAMPED OSCILLATOR
𝜔0 =
𝑏
2𝑚
As a result 𝜔0 = 0
KEY POINT: Does not oscillated, reaches equilibrium the fastest.
OVERDAMPED OSCILLATOR
𝜔0 is less than
𝑏
2𝑚
As a result, 𝜔0 is a negative value.
KEYPOINT: No oscillation, takes a long time to reach equilibrium.

5. Citation
Hawkes et al., (2015). Physics for Scientists and Engineers: An Interactive Approach. Toronto: Nelson
Education Ltd.