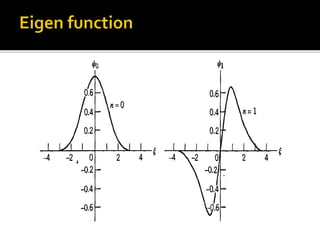
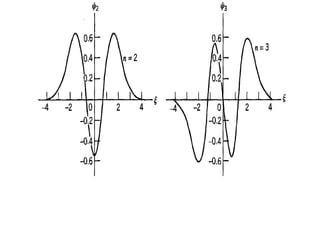
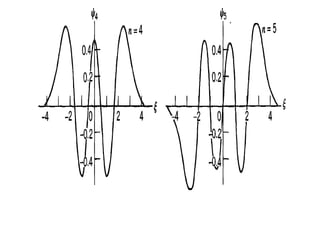
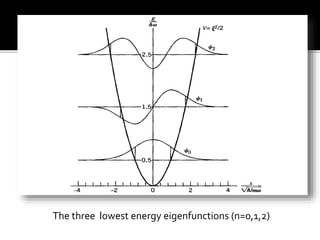
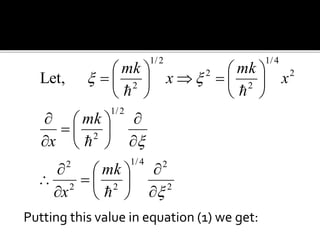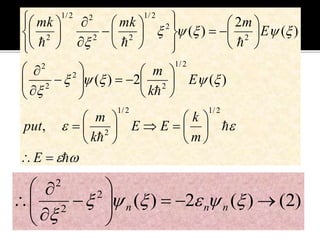The harmonic oscillator played a key role in early quantum theory. Planck, Einstein, and others assumed that atoms, radiation, and solids behaved like quantum harmonic oscillators to explain phenomena like blackbody radiation and heat capacities. This led to the development of quantum theory for electromagnetic and mechanical oscillators. Solving the Schrödinger equation for the harmonic oscillator yields discrete energy levels and eigenfunctions that describe its quantized energy spectrum.

1. Ahmed Haider Ahmed
s.M.Sc. Physics – ASU

3. The harmonic oscillator played a leading role in the
development of quantum mechanics. In 1900, Planck made the bold
assumption that atoms acted like oscillators with quantized energy when
they emitted and absorbed radiation; in 1905, Einstein assumed that
electromagnetic radiation acted like electromagnetic harmonic
oscillators with quantized energy; and in 1907, Einstein assumed that the
elastic vibrations of a solid behaved as a system of mechanical oscillators
with quantized energy. These assumptions were invoked to account for
black body radiation, the photoelectric effect and the temperature
dependence of the specific heats of solids. Subsequently, quantum
theory provided a fundamental description of both electromagnetic and
mechanical harmonic oscillators.

4. So, the potential energy will be:





kxdxxv
Fdxxv
kxF
)(
)(
2
2
1
)( kxxv 
Substituting in Schrödinger equation :

5. Schrödinger equation will be:
  )()()(
2
2
2
rErrv
m
 

In x direction
)()(
2
1
2
2
2
22
xExkx
xm
 










)1()(
2
)( 2
2
22
2









xE
m
xx
mk
x



6. 2
24/1
22
2
2/1
2
2
4/1
2
2
2/1
2
Let,










































mk
x
mk
x
x
mk
x
mk
Putting this value in equation (1) we get:

7. 





































































E
m
k
EE
k
m
put
E
k
m
E
mmkmk
2/12/1
2
2/1
2
2
2
2
2
2
2/1
22
22/1
2
,
)(2)(
)(
2
)(
)2()(2)(2
2
2









 

nnn

8.  The quantum energy spectrum consist of
discrete values according to energy levels
 n() is the angular function for state n and En
is the energy of the state n
 The problem now is to determine n , n

9. )(1
),(1
2
2
2
2
2
2
II
I


































































Applying factorization methods on equation (2).

10. )3()()12()( 










































 nnn
(3)with(2)equationcomparing
)(
:beillsolution wits
0)(
2
2
1
by
en
n














(*)11   nn 

11. (4)with(2)equationcomparing
)(
:beillsolution wits
0)(
2
2
1
by
en
n















)4()()12()( 











































nnn
(**)11   nn 

12. (Creation))()(
,ion)(Annihilat)()(
1
1
























nn
nn

13. This the quantized energy of harmonic oscillator
nn
nn
n





0
1
1n
1
1



Ebut,







2
1
nEn n = 0,1,2,3,….

17. The three lowest energy eigenfunctions (n=0,1,2)

18.  Introduction to Quantum Mechanics: A. C. Phillips, Physics
and Astronomy Dept. University of Manchester.
 Lecture notes in quantum mechanics by Dr. Mahmoud Salah
, Physics Dept., University of Minia, 2010
 Quantum Mechanics 3rd EDITION : Eugen Merzbacher
University of North Carolina at Chapel Hill.