The document covers the fundamentals of oscillations in engineering physics, including types of harmonic motion such as simple harmonic motion and damped harmonic motion. It further explores different cases of damping (over damped, critically damped, and under damped), their equations, and the concept of forced harmonic oscillators and resonance. Key ideas include the effects of damping on amplitude and frequency, as well as the quality factor which measures oscillation sharpness and damping levels.

1. Engineering Physics
Module I
1
OSCILLATIONS

2. Contents
2
Periodic Motion
Simple Harmonic
Motion
Damped
Harmonic Motion
Damped Harmonic Motion
Case 1: Over
damped
Damped Harmonic Motion
Case 2: Critically
damped
Damped Harmonic Motion
Case 3: Under
damped
Relaxation Time Q-factor
Forced Harmonic
Oscillator
Forced Harmonic Oscillator
Amplitude
Resonance
Forced Harmonic Oscillator
Sharpness of
Resonance
Forced Harmonic Oscillator
Q-factor at
Resonance
Electrical
Oscillator
Comparison of
electrical and
mechanical
oscillator
 Click on each content to go to the section
Table of Contents Next Page
Previous page

3. Periodic Motion
3
Periodic motion is any motion that is repeated in equal intervals of time

4. Periodic Motion: Oscillation vs Vibration
4
Vibration
Only part of the body executes to and fro motion about a mean position .
Oscillation
The whole body executes to and fro motion about a mean position .

5. Simple Harmonic Motion (SHM)
5
Simple harmonic motion is an oscillation where the restoring force is directly proportional
to the displacement from mean position and is always directed towards mean position.

6. 6
Force acting on a simple harmonic oscillator is
Restoring force = - Cx where C is the force constant
m
d2
x
dt2
= −Cx
Force equation of SHM is
--------------------------(1)
d2
x
dt2
+ ωo
2
x = 0 -------------------------(2)
where is the natural angular frequency
ωo = ඨ
C
m
Dividing through out with ‘m’
d2x
dt2
+
C
m
x = 0
Simple Harmonic Motion
where A is the maximum displacement and ϕ is the initial phase
Equation (2) is the differential equation of simple harmonic oscillator. General solution of this equation is
sin(ωot + φ)

7. Simple Harmonic Motion
7
 SHM will continue to be in motion indefinitely
sin(ωot + φ)
This term will vary between +1 and -1, sinusoidally
Value of ‘x’ will vary between +A and -A, sinusoidally
 In real world, simple harmonic motion (also called free harmonic oscillator) does not exist since there is
always some sort of resistive force acting on the oscillator

8. Damped Harmonic Motion
8
 Frictional forces or other external forces can lead to a loss (dissipation) of energy of an oscillator. This phenomenon is
called damping.
 Simple harmonic motion under the effect of damping forces is known as damped harmonic oscillation.
For smaller velocities, damping force is proportional to the velocity and is acting in opposite direction of the displacement.
Damping force w  is the damping coefficient
Force equation of a damped harmonic oscillator is
= 0
w C is the restoring force constant
Damping force
Consider a damped harmonic oscillator with mass ‘m’. Forces acting on a damped harmonic oscillator are damping force
and restoring force.

9. Damped Harmonic Motion
9
Dividing through out with ‘m’
d2
x
d t2
+2 k
dx
dt
+ωo
2
x=0
Equation (1) is the differential equation of damped harmonic oscillator.
---------------------------------------------------------- (1)
where k = is the damping constant and is the natural angular frequency in the absence of damping.
Let x =A be a possible solution of equation (1).
dx
d 𝑡
= A e
 t
d2
x
d t 2
=2 A et
Substituting in equation (1)
= 0

10. Damped Harmonic Motion
10
= 0
) = 0
Since A cannot be zero,
= 0
c = 0
x=
− b ± √b2
− 4 ac
2 a
=
− 2 k ± √4 k
2
− 4 ωo
2
2
=
−2 k ± 2 √k
2
− ωo
2
2
=− k ± √k
2
− ωo
2
1=−k+√k2
−ωo
2
2=−k −√k2
−ωo
2
Therefore general solution of equation (1) is of the form
x= A1 + A2
x= A1e
(−k+√k
2
−ωo
2
)t
+A 2e
(−k−√k
2
−ωo
2
)t --------------------------------- (2)

11. Damped Harmonic Motion
11
x= A1e
(− k +√k
2
− ωo
2
)t
+A 2e
(−k − √k
2
−ωo
2
)t
]
w A1 and A2 are two constants that depends on initial conditions of motion
--------------------------------- (2)
---------------------------- (3)
Displacement of the oscillator
from mean position at time ‘t’.
k is the damping constant.
ω0 is the natural angular frequency in the
absence of damping
Depending on relative values of k and ω0 we have three different cases.
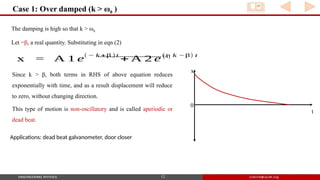
1. k > ω0 Over damped
2. k = ω0 Critically damped
3. k < ω0 Under damped

12. Case 1: Over damped (k > ω0 )
12
The damping is high so that k > ω0
Let =β, a real quantity. Substituting in eqn (2)
x = A 1 e
(− k+β )t
+ A 2 e
(− k −β) t
-------------------------------- (4)
Since k > β, both terms in RHS of above equation reduces
exponentially with time, and as a result displacement will reduce
to zero, without changing direction.
This type of motion is non-oscillatory and is called aperiodic or
dead beat.
x
t
0
Applications: dead beat galvanometer, door closer

13. Case 2: Critically damped (k = ω0 )
13
When k = ω0, eqn (3) becomes
) = B where B= --------------------------------- (5)
Since above equation has only one constant, it does not form solution of a second order differential equation.
Therefore, we shall put = h, a very small positive quantity (h→0).
]
}
]
]
]
where D= A1+A 2 and E=(A1− A2)h
x
t
0
Initially the displacement increases slightly due to the factor D+Et. But as time elapses, the exponential term become
dominant factor and as a result displacement will returns continuously to zero, without changing direction, even faster than
over damped condition. This type of motion is non-oscillatory or aperiodic.
Applications: speedometer, multimeter, pressure gauge

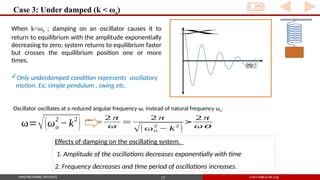
14. Case 3: Under damped (k < ω0 )
Whendamping is very low ,k<ω 0
= = i and i=
Substituting in eqn (3)
]
]
]
14
The displacement ‘x’ being a real quantity, both must be real and so both A1 and A2 are complex.
Let φ
and = φ
]
x =a 0 e−kt
sin ⁡¿
sin ⁡(A+B)=sinAcosB + cosAsinB
]
---------------------------- (6)

15. Case 3: Under damped (k < ωo)
15
When k<ω0 ; damping on an oscillator causes it to
return to equilibrium with the amplitude exponentially
decreasing to zero; system returns to equilibrium faster
but crosses the equilibrium position one or more
times.
𝑡𝑖𝑚𝑒(𝑡)
x
Only underdamped condition represents oscillatory
motion. Ex; simple pendulum , swing etc.
Oscillator oscillates at a reduced angular frequency ω, instead of natural frequency ωo.
ω=√(ωo
2
−k2
) T =
2 π
ω
=
2 π
√(ωo
2
− k
2
)
>
2 π
ω 𝑜
Effects of damping on the oscillating system.
1. Amplitude of the oscillations decreases exponentially with time
2. Frequency decreases and time period of oscillations increases.

16. Energy of Damped Harmonic Oscillator
16
Energy of harmonic oscillator is proportional to square of the amplitude. In case of a damped harmonic oscillator, amplitude is
where Eo is the initial energy of the oscillator at t = 0
The energy of oscillator decreases exponentially with time. Consider the case when
Eo e
−2 k
2 k
=
Eo
e
Et= Eo e− 2 kt
Et ∝(ao e
−kt
)
2
Time taken by the oscillator to reduce the energy to 1/e times its initial value is called relaxation time
of oscillator.
Relaxation Time
Relaxation Time
E 1
2 k
=¿

17. Quality Factor of Damped Harmonic Oscillator
17
 Quality factor (Q-factor) is defined as 2π times the ratio of energy stored to the average energy lost per cycle
𝐐=𝟐𝛑
𝐄𝐧𝐞𝐫𝐠𝐲𝐬𝐭𝐨𝐫𝐞𝐝
𝐄𝐧𝐞𝐫𝐠𝐲𝐥𝐨𝐬𝐭 𝐩𝐞𝐫𝐩𝐞𝐫𝐢𝐨𝐝
 Q-factor a dimensionless quantity and it is a measure of lack of damping of an oscillator.
 High Q means that the oscillation is lightly damped and larger the number of oscillations the system can
perform before coming to rest.
 The system performs Q/2π oscillations during relaxation time.

18. Quality Factor of Damped Harmonic Oscillator
18
For small value of damping, k2
can be neglected.
ω=√(ωo
2
−k
2
)
=
k =
𝑄=
√C
m
m
γ
Frequency x time = number oscillation in that time interval
 Oscillator will execute number of oscillations in the
relaxation time.
 Oscillator will execute number of oscillations when its
energy is reduced to (1/e)th
of its initial energy.

19. 19
Forced or Driven Harmonic Oscillator
External driving force where Fo is amplitude and p/2π is the frequency of applied periodic force
Force equation of a forced harmonic oscillator is
m
d2
x
d t
2
=− Cx − γ
dx
dt
+ F o sinpt
Forces acting on a forced harmonic oscillator are
Restoring force = - Cx where C is the force constant
Damping force w  is the damping coefficient
m
d2
x
d t
2
+γ
dx
dt
+Cx=F o sinpt
Every oscillating and vibrating system has its own natural frequency of oscillation. When excited, it will oscillate with its
natural frequency. If and external periodic force (driving force) is continuously applied, the body will continuously
oscillate with the frequency of applied force.
An oscillator which is forced to oscillate with the frequency of applied periodic force is called forced or driven harmonic
oscillation.

20. 20
Forced or Driven Harmonic Oscillator
d2
x
d t2
+2 k
dx
dt
+ωo
2
x=f o sinpt - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - (1)
Equation (1) is the differential equation of forced harmonic oscillator.
where k = is the damping constant
is the natural angular frequency of the oscillator.
fo = is a constant
Eqn (1) is a linear differential equation of second order and its solution contains two parts: a complementary function
and particular integral
1. Complementary function is the solution of
d2
x
d t
2
+2 k
dx
dt
+ωo
2
x=0
)
ω=√(ωo
2
−k2
)
where
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - (2)
Dividing through out with ‘m’
d2
x
d t
2
+
γ
m
dx
dt
+
C
m
x=
F o
m
sinpt

21. 21
Forced or Driven Harmonic Oscillator
2. Particular Integral is found by trial
At steady state, the body oscillates with the same frequency as the driving force, but the displacement lag behind applied
force. So particular integral can be of the form
x = A sin( pt −θ) - - - - - - - - - - - - - - - -- - - - - - (3)
where A is the amplitude of maintained oscillations
θ is the phase lag of displacement behind the applied force
d x
d t
= p A cos(pt −θ)
d 2x
d t 2
= − p2 A sin( pt −θ)
d2
x
d t
2
+2 k
dx
dt
+ωo
2
x=f o sinpt
− p 2 A sin( pt −θ)+2 kpA cos( pt −θ)+ωo
2
A sin( pt − θ)=f o sinpt
- - - - - - - - - - - - - - - - - - - - - - (4)
- - - - - - - - - - - - - - - - - - - - - (5)
Substituting from eqns (3), (4) and (5) in eqn (1) - - -- (1)

22. 22
Forced or Driven Harmonic Oscillator
− p 2 A sin( pt −θ)+2 kpA cos( pt −θ)+ωo
2
A sin( pt − θ)=f o sinpt
)
Comparing coeffieicents of sin ( pt −θ) ∧cos ( pt − θ)
(ω¿¿o2
− p2)A=focosθ¿
2kpA=f osin θ
- - - - - - - - - - - - - - - - - - - - - - (6)
- - - - - - - - - - - - - - - - - - - - - - (7)
Divide eqn(7)witheqn(6)
f osinθ
f ocosθ
=
2kpA
(ω¿¿ o
2
− p2) A¿
tan θ=
2 kp
ωo
2
− p 2
(ω¿¿o2
− p2)2 A2+4k2p2 A2=fo2cos2θ+f o2sin2θ¿
] =
A2=
f o2
(ω¿¿o
2
− p2)2+4k2p2¿
Squaring∧addingeqn(7)∧eqn(6)
A=
f o
√(ω¿¿o
2
− p2)2+4k2p2¿
- - - - - (8)

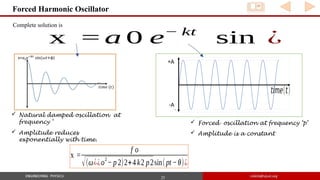
23. 23
Forced Harmonic Oscillator
So particular integral is
x =
f o
√(ω¿¿o2
− p2)2+4k2 p2sin(pt−θ)¿
- - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - (9)
Complete solution of equation (2) is {substituting from eqns (2) and (9)}
x = a o e− kt
sin ⁡
¿
where θ=tan
− 1
[ 2 kp
ωo
2
− p 2 ]

24. 24
Forced Harmonic Oscillator
Complete solution is
x = a 0 e− kt
sin ⁡¿
First term represents natural damped oscillation at frequency ‘ with amplitude reducing exponentially with time. Second
term represents forced oscillation at frequency ‘p’, with a constant amplitude ‘A’. Initially both vibrations will ebe present,
but with the passage of time, the first term vanishes and the motion of the body can be completely represented by the
second term . So the displacement of the forced harmonic oscillator is given by the equation
x =
f o
√(ω¿¿o2
− p2)2+4k2 p2sin(pt−θ)¿
Refer next slide

25. 25
Forced Harmonic Oscillator
Complete solution is
x = a 0 e− kt
sin ⁡¿
 Natural damped oscillation at
frequency ‘  Forced oscillation at frequency ‘p’
 Amplitude reduces
exponentially with time.
 Amplitude is a constant
x =
f o
√(ω¿¿o2
− p2)2+4k2 p2sin(pt−θ)¿
-1
0
1
𝑡𝑖𝑚𝑒(𝑡)
+A
-A

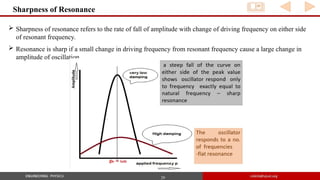
26. 26
Amplitude Resonance
Resonance is the phenomenon by which the amplitude of the forced harmonic oscillator becomes maximum at
a particular driving frequency which is very close to its natural frequency.
Frequency at which resonance occur is known as resonant frequency (pR).
A=
f o
√(ω¿¿o
2
−p2)2+4k2p2¿
Amplitude of a forced harmonic oscillator is given by
Value of A =Amax when the denominator is minimum.
]= 0
−2 (ω ¿¿ o2
− p 2) x 2 p+ 8 k 2 p=0 ¿
−(ω ¿¿ o2
− p 2) x 4 p+ 2 k 2 x 4 p=0 ¿
− (ω ¿¿ o2
− p 2)+ 2 k 2= 0 ¿
p 2= ω o
2
− 2 k 2
p=p R=√ωo
2
− 2 k 2
is the resonant frequency

27. 27
Amplitude at Resonance
Amax=
f o
√(ω¿¿o2
− p R2)2+4k 2 pR 2¿
When p=pR
A max=
f o
√[ω ¿¿ o
2
−(√ωo
2
−2 k 2)2]2+4 k 2 p R 2¿
A max =
f o
2 k √ k 2 + p R 2
For low damping k2
can be neglected and so
p = p R = ω o
𝐀𝐦𝐚𝐱=
𝐟 𝐨
𝟐𝐤 𝛚𝐨
=
𝐟 𝐨𝛕
𝛚𝐨 pR
Low damping
Medium
damping
High damping

28. 28
Quality Factor at Amplitude Resonance
=
A max=
f o
2 kωo
=
f o τ
ωo
Q
Q
Quality Factor at amplitude resonance is defined as the ratio of amplitude at resonance to
amplitude at zero driving frequency.
Q

29. 29
Sharpness of Resonance
 Sharpness of resonance refers to the rate of fall of amplitude with change of driving frequency on either side
of resonant frequency.
 Resonance is sharp if a small change in driving frequency from resonant frequency cause a large change in
amplitude of oscillation.

30. 30
LCR Circuit as an Electrical Analogue of Mechanical Oscillator
V L= L
di
dt
=L
d 2q
dt 2
V R=Ri=R
dq
dt
V C=
q
C
L
d 2 q
dt 2
+R
dq
dt
+
q
C
=Vapplied
m
d2
x
d t
2
+γ
dx
dt
+ kx=F applied
Potential difference across inductor
Potential difference across resistor
Potential difference across capacitor
The sum of Potential difference across each circuit element is equal to the applied voltage
Force equation of forced harmonic oscillation of an oscillator of mass ‘m’ is
Above force equation is similar to voltage equation of LCR circuit. The electric charge oscillates between capacitor (C) and
inductor (L) through resistor (R) similar to mechanical oscillations of the oscillator. The resistance (R) causes the dissipation
of electric energy where as damping causes dissipation in mechanical oscillator.

31. 31
Comparison of Mechanical and electrical Oscillator
No. Quantity in Mechanical Oscillator Quantity in Electrical Oscillator
1 Mass (m) Inductance (L)
2 Displacement (x) Charge (q)
3 Damping Coefficient () Resistance (R)
4 Velocity () Current (i=)
5 Force Constant (k) Reciprocal of Capacitance (1/C)
6 Potential Energy () Energy stored in Capacitor ( = )
7 Kinetic Energy () Energy stored in Inductor()
8 Angular frequency Angular frequency
9 Quality factor Q Quality factor Q

32. 32