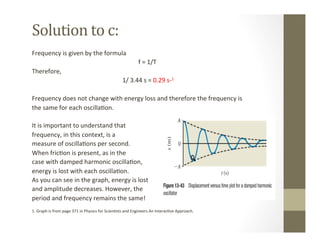
This document provides the solution to calculating properties of a damped harmonic oscillator. It is a 3 kg block attached to a spring with a 10 N/m constant. The initial energy is 0.300 J and 0.140 J is lost after 4 oscillations. The damping constant b is calculated to be 0.167 kg/s. The percentage decrease in amplitude after 4 oscillations is 31.8%. The frequency is calculated to be 0.29 s-1 for each oscillation, as the frequency does not change even as energy is lost and amplitude decreases over multiple oscillations.

1. Damped Harmonic
Oscillator

2. Question:
• A
damped
harmonic
oscillator
of
a
block
has
mass
3.00
kg
and
a
spring
constant
10.0
N/m.
The
ini<al
total
energy
of
the
oscillator
is
E(0)
=
0.300
J
and
the
amount
of
energy
lost
during
four
oscilla<ons
is
0.140
J.
Assuming
that
the
damping
force
is
of
the
form
FD,x
=
-­‐bvx,
calculate1:
a) The
value
of
the
damping
constant
b) The
percentage
decrease
in
amplitude
aLer
four
oscilla<ons.
c) The
frequency
of
the
fourth
oscilla<on.
How
does
the
frequency
of
the
fourth
oscilla<on
compare
to
the
frequency
of
the
first
oscilla<on?
1.
Ques<on
was
derived
from
example
13-­‐11
in
Physics
for
Scien<sts
and
Engineers
An
Interac<ve
Approach.

3. Solution
to
a:
First
we
must
calculate
the
period.
Since
we
are
given
the
amount
of
energy
lost
during
four
oscilla<ons
to
be
0.150
J
we
can
determine
that
the
damping
is
weak
and
therefore
assume
that
wD
=
w0.
T
=
2π/w0
=
2π√(m/k)
=
2π√(3.00
kg
/
10.0
N/m)
=
3.44
s
To
find
the
damping
constant,
we
must
solve
for
b
in
the
following
equa<on:
E(4T)
=
E(0)e-­‐4bT/m
We
have
the
values
for
E(0),
t,
and
m,
but
we
need
to
find
the
value
for
E(4T)
so
that
we
can
use
the
equa<on
to
isolate
for
b.

4. Solution
to
a
cont’d:
We
know
that,
E(4)
=
E(0)
–
Energy
lost
in
4
oscilla<ons
E(4)
=
0.300
J
–
0.140J
=
0.160J
Plugging
this
back
into
the
previous
equa<on
we
get,
E(4T)
=
E(0)e-­‐4bT/m
0.140
J
=
0.300
J
x
e-­‐4b
x
3.44
s/
3.00
kg
0.467
=
e-­‐4b
x
3.44
s/
3.00
kg
ln
(0.467)
=
(-­‐4b
x
3.44
s)
/
3.00
kg
b
=
ln
(0.467
J)
x
3.00
kg
=
0.167
kg/s
(-­‐4
x
3.44
s)

5. Solution
to
b:
Now
that
we
know
the
damping
constant,
we
can
use
the
following
equa<on
to
relate
the
amplitude
at
t
=
0s
and
the
amplitude
aLer
four
oscilla<ons.
Let
x
=
the
percentage
of
the
ini<al
amplitude
aLer
four
oscilla<ons
A(4T)
=
A*e-­‐4bT/2m
=
x*A
e-­‐4bT/2m
=
x
e(-­‐4
x
0.167
kg/s
x
3.44
s
)
/
(2
x
3.00
kg)
=
0.682
Now
we
know
the
percentage
of
the
ini<al
amplitude
that
remains
aLer
four
oscilla<ons.
However,
the
ques<on
is
asking
the
percentage
of
amplitude
that
is
lost
aLer
four
oscilla<ons.
Thus,
1
–
0.682
=
0.318
or
31.8%
of
amplitude
height
is
lost
during
the
four
oscilla<ons.

6. Solution
to
c:
Frequency
is
given
by
the
formula
f
=
1/T
Therefore,
1/
3.44
s
=
0.29
s-­‐1
Frequency
does
not
change
with
energy
loss
and
therefore
the
frequency
is
the
same
for
each
oscilla<on.
It
is
important
to
understand
that
frequency,
in
this
context,
is
a
measure
of
oscilla<ons
per
second.
When
fric<on
is
present,
as
in
the
case
with
damped
harmonic
oscilla<on,
energy
is
lost
with
each
oscilla<on.
As
you
can
see
in
the
graph,
energy
is
lost
and
amplitude
decreases.
However,
the
period
and
frequency
remains
the
same!
1.
Graph
is
from
page
371
in
Physics
for
Scien<sts
and
Engineers
An
Interac<ve
Approach.