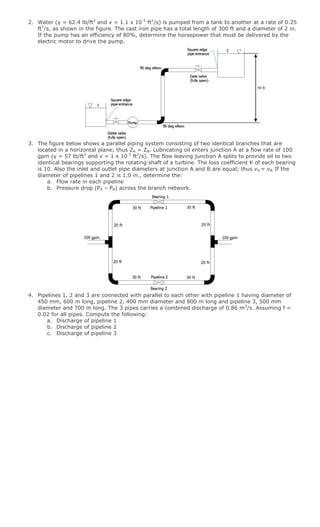
The document discusses flow of fluids in pipelines including: 1. Laminar and turbulent flow and the factors that determine the transition between the two such as Reynolds number. 2. Methods for calculating head losses and pressure drops in pipes due to friction including the Darcy-Weisbach equation. 3. Factors that affect friction losses such as pipe roughness, geometry, and flow characteristics. 4. Analysis of flow in non-circular pipes using concepts like hydraulic diameter. 5. Examples of problems calculating flow characteristics like velocity and pressure changes in series and parallel pipe networks.

1. LECTURE UNIT NO. 8
FLOW OF VISCOUS FLUIDS IN PIPELINES
 Laminar flow
Illustration:
In Laminar, streamline or viscous flow, the fluids are moving in paths parallel to the pipe
centerline.
 Turbulent flow
Illustration:
In the beginning of turbulent flow, the movement of each particle becomes random and fluctuates
up and down in a direction perpendicular as well as parallel to the centerline of the pipe.
CIRCULAR PIPES
REYNOLDS NUMBER, NR
Experiment performed by Osborne Reynolds (British Engineer) in 1883 to determine the conditions
governing the transition from laminar to turbulent flow.
v = the fluid velocity, m/s
D = pipe inside diameter, m
ρ = fluid density, kg/m3
μ = absolute viscosity of the fluid, N/m2 – s or Pa - s
Since: kinematic viscosity v equals absolute viscosity μ divided by density ρ.
If NR ≤ 2000, the flow is laminar
If NR ≥ 4000, the flow is turbulent
If 2000 < NR < 4000, the flow can be either laminar or turbulent (critical zone).
For energy loss calculation and the flow is in critical zone, assume the flow to be turbulent.
Total Head Loss or Fluid Frictional Losses
HT = hf1 + hp + hf2 + hetc.
hf1 = pipe friction loss at suction
hp = head loss at the pump
hf2 = pipe friction loss at discharge
PIPE FRICTION LOSS, h
The Darcy-Weisbach Equation
The Darcy-Weisbach equation can be used for either laminar and turbulent flow depending on how
friction factor f is determined.
L = pipe equivalent length (Page 97)
Using Mechanical Engineering Tables and Chartd (SI units) 4th Edition
L = Lpipe + Lelbows + Lvalves + Lfittings + Letc.

2. Equivalent Length Method
Applicable only if the system has equal velocities (that is head losses across valves and fittings are
equal for the same flow rate and pipe diameter).
Friction Factor, f
Usual range: 0.016 – 0.023
Use: 0.02 if not given
Friction factor for laminar flow
Friction factor for turbulent flow
ε
D
ε = pipe inside surface roughness or absolute roughness
Table 8.1 Values of absolute roughness ε for new pipes
Page 225 Fluid Mechanics with Engineering Applications SI Metric Edition
By: Dougherty, Franzini and Finnemore
Relative roughness can also be determined using Figure 8.12 Page 227
Fluid Mechanics with Engineering Applications SI Metric Edition
By: Dougherty, Franzini and Finnemore
To determine the Friction Factor f, Plot Reynolds Number vs. Relative Roughness using MOODY DIAGRAM
Figure 8.11 Friction factor for pipes (Moody Diagram)
Page 226 Fluid Mechanics with Engineering Applications SI Metric Edition
By: Dougherty, Franzini and Finnemore
LOSSES IN VALVES AND FITTINGS
k = loss coefficient factor of the valve or fitting
Table 8.3 Values of loss factors for pipe fittings
Page 239 Fluid Mechanics with Engineering Applications SI Metric Edition
By: Dougherty, Franzini and Finnemore
LOSSES IN PIPE ENTRANCES, EXITS, CONTRACTIONS AND EXPANSION
Pipe Entrances
Square-edged kL = 0.5
Well-rounded kL = 0.04
Reentrant kL = 1.0
Pipe Exits
Square-edged kL = 1.0
Rounded kL = 1.0
Reentrant kL = 1.0

3. Sudden Contraction
Sudden Expansion
Gradual Expansions
NONCIRCULAR PIPES
Hydraulic Diameter, Dh
w
d
A = cross-sectional area of pipe
P = perimeter of the pipe

4. Dh for rectangular pipe of depth d and width d:
Dh for square duct of side s:
Dh for circular pipe of diameter D:
Hence, Darcy-Weisbach equation is still valid for non circular pipe.
Determination of f for Laminar Flow in Noncircular Pipe
C = empirical constant, depends on the cross sectional shape
C = 64 for circular pipe
C = 57 for square (d/w = 1)
NRh = Reynolds Number
If NRh ≤ 2000, the flow is laminar
If NRh ≥ 4000, the flow is turbulent
If 2000 < NRh < 4000, the flow can be either laminar or turbulent (critical zone).
Reynolds Number for Noncircular Pipes
Noncircular Pipe Head loss
f = C/NRh for laminar flow
f using Moody Diagram for turbulent flow
Problems:
1. A pipe has a diameter of 20 mm and a length of 80 m. A liquid having a kinematic viscosity of 4 x
10-5 m2/s is flowing thru the pipe at a viscosity of 3 m/s. (a) Compute for the Reynolds number (b)
determine the friction factor (c) compute for the head loss of the pipe.
2. Oil flows thru a 50 mm dia. Pipe having a head loss if 12 m. The length of pipe is 120 m. long. If
the oil has a Reynolds number equal to 1600, (a) Compute the velocity of the oil flowing in the pipe
(b) What is the kinematic viscosity of oil in m2/s (c) What is equivalent viscosity of oil in strokes.
3. SAE oil ρ = 869 kg/m3 flows through a cast iron pipe at a velocity of 1.0 m/s. The pipe is 45 m.
long and has a diam. Of 150 mm. Absolute viscosity μ = 0.0814 Pa-s. Compute the following: (a)
Reynolds number (b) Determine the type of flow (c) Head loss due to friction.
4. The industrial scrubber B as shown in the figure consumes water (v =0.113 x 10-5 m2/s) at the rate
of 0.1 m3/s. I the pipe is 150 mm commercial pipe and f = 0.016, compute the following (a)
Reynolds number (b) The total head loss from A to B (c) The necessary tank pressure.

5. 295m
25m
150m
300m
5. The bunker storage tank is filled with oil up to a height of 6 m. and the pressure at top of oil
surface is 34 kPa. A 150 mm discharge pipeline is connected at the bottom of the tank having a
length of 135 m. The point of withdrawal is 9 m. below the bottom of the tank and the pipe
discharges freely into the oil tanker for disposal to the different industrial plants utilizing oil for
their production. Viscosity of oil is 500 centistroke and the oil has a specific gravity of 0.80.
Assuming coefficient of discharge C = 0.90. (a) Determine the rate of flow of oil to the tank. (b)
Determine the Reynolds number (c) Determine the time to fill up one tanker if it has a capacity of
14 m3.
SERIES AND PARALLEL PIPING SYSTEM
There are two basic categories of fluid piping systems, the series and parallel.
I. Series
a. Total HL = hf1 + hf2 + hf3
b. Q1 = Q2 = Q3
II. Parallel
a. Total HL = hf1 + hf2 + hf5
b. Q1 = Q5
c. Q1 = Q2 + Q3 + Q4
d. hf2 = hf3 = hf4
Problems:
1. Find the pressure drop P1 – P2 across the entire pipeline shown in the figure. The flow rate
of water (γ = 9800 N/m3 and v = 1 x 10-6 m2/s) is 0.05 m3/s and the pipe diameter is 100
mm. The elevation difference between points 1 and 2 is 4 m and the total length of the cast
iron pipe between points 1 and 2 is 30 m. K90°elbow = 0.75

6. 2. Water (γ = 62.4 lb/ft3 and v = 1.1 x 10-5 ft2/s) is pumped from a tank to another at a rate of 0.25
ft3/s, as shown in the figure. The cast iron pipe has a total length of 300 ft and a diameter of 2 in.
If the pump has an efficiency of 80%, determine the horsepower that must be delivered by the
electric motor to drive the pump.
50 ft
3. The figure below shows a parallel piping system consisting of two identical branches that are
located in a horizontal plane; thus ZA = ZB. Lubricating oil enters junction A at a flow rate of 100
gpm (γ = 57 lb/ft3 and v = 1 x 10-3 ft2/s). The flow leaving junction A splits to provide oil to two
identical bearings supporting the rotating shaft of a turbine. The loss coefficient K of each bearing
is 10. Also the inlet and outlet pipe diameters at junction A and B are equal; thus vA = vB. If the
diameter of pipelines 1 and 2 is 1.0 in., determine the:
a. Flow rate in each pipeline
b. Pressure drop (PA – PB) across the branch network.
4. Pipelines 1, 2 and 3 are connected with parallel to each other with pipeline 1 having diameter of
450 mm, 600 m long, pipeline 2, 400 mm diameter and 800 m long and pipeline 3, 500 mm
diameter and 700 m long. The 3 pipes carries a combined discharge of 0.86 m 3/s. Assuming f =
0.02 for all pipes. Compute the following:
a. Discharge of pipeline 1
b. Discharge of pipeline 2
c. Discharge of pipeline 3

7. FLOW OF GASES IN PIPES
Analysis Technique for Evaluating Pressure Losses in Compressed Air Lines
1. Air is supplied to a small pneumatic hand drill via a flexible hose of ½ inch inside diameter.
Included in the line are two 90° elbows, one fully open gate valve, one ball check valve (K L = 2.2),
and one line flow tee. The air receiver contains compressed air at 100 psig and a temperature of 80
°F. The rate of air consumption of the drill is 5 scfm. Determine the maximum allowable length of
hose that may be used if the drill requires an air pressure of 95 psig. The relative roughness of the
hose is 0.002.
P1
1
SPEED OF SOUND AND MACH NUMBER
Speed of Sound
The speed of sound is defined as the rate at which a pressure disturbance propagates in a medium
such as a liquid or a gas. The speed of sound is greater in liquid than in a gas.
c = speed of sound
β = bulk modulus of liquid
ρ = density of liquid
For Gasses:
k = gas isentropic exponent
k = 1.4 for air, hydrogen, nitrogen and oxygen
k = 1.3 for carbon dioxide and methane
k = 1.66 for helium
P = absolute pressure
ρ = density of air
R = gas constant
R = 1716 ft-lbf/lbm - °R = 0.287 KJ/kg – K
T = absolute temperature
Isentropic Process
P1V1K = P2V2K
Mach number
Mach number (NM) is defined as the velocity (v) of a fluid (or velocity of an object in the fluid)
divided by the speed of sound (c) in the same fluid.
if NM < 1 Subsonic flow
NM = 1 Sonic flow
NM > 1 Supersonic flow
1. A commercial jet airliner travels at a speed of 500 mph at an altitude of 35,000 ft where the
temperature is -65°F. Determine the Mach number of the airliner.