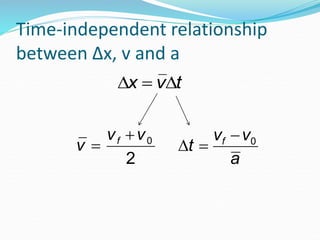
The document discusses equations for calculating velocity, acceleration, displacement, and time for objects moving with constant velocity or uniform acceleration. It provides the key equations: 1) For constant velocity, average velocity (v) equals displacement (Δx) over time (Δt), and displacement equals velocity times time. 2) For uniform acceleration, final velocity (vf) equals initial velocity (v0) plus acceleration (a) times time (Δt), and displacement equals initial velocity times time plus one-half acceleration times time squared. 3) A single equation relates displacement, initial velocity, final velocity, and acceleration, which can be rearranged to solve for any of those variables.

2. Constant velocity
Average velocity equals the slope of a position vs time
graph when an object travels at constant velocity.

v 
x
t

3. Displacement when object
moves with constant velocity
The displacement is the area under a velocity vs time
graph

x  v t

4. Uniform acceleration
This is the equation of the line of the velocity vs time graph
when an object is undergoing uniform acceleration.
The slope is the
acceleration
The intercept is the
initial velocity
vf  at v0

5. Displacement when object
accelerates from rest
 Displacement is still the area under the velocity vs
time graph. Use the formula for the area of a triangle.
x  1
2
vt
 From slope of v-t graph:
v  a t
 Now, substitute for Δv:
x  1
2
a t  t
x  1
2
a (t )2

6. Displacement when object
accelerates with initial velocity
Break the area up into two parts:
 the rectangle representing
displacement due to initial velocity
 and the triangle representing
displacement due to acceleration

x  v0t
x  1
2
a(t )2

7. Displacement when object
accelerates with initial velocity
Sum the two areas:
x  v0 t  1
2
a( t )2
Or, if starting time = 0, the
equation can be written:

x  v0t  1
2
at 2

8. Time-independent relationship
between Δx, v and a
Another way to express average velocity is:

v 
x
t

v 
vf v0
2

9. Time-independent relationship
between Δx, v and a
We have defined acceleration as:
a 
This can be rearranged to:
v
t
and then expanded to yield :


t 
v
a
t 
vf v0
a

10. Time-independent relationship
between Δx, v and a
Now, take the equation for displacement
and make substitutions for average velocity and Δt

x  v t

11. Time-independent relationship
between Δx, v and a

x  v t

v 
vf v0
2

t 
vf v0
a

12. Time-independent relationship
between Δx, v and a

x  v t

x 
vf  v0
2

vf v0
a

13. Time-independent relationship
between Δx, v and a
Simplify

x 
vf  v0
2

vf v0
a
x 
2 v0
vf
2
2a

14. Time-independent relationship
between Δx, v and a
Rearrange

x 
2 v0
vf
2
2a

2  v0
2a x  vf
2

15. Time-independent relationship
between Δx, v and a
2  v0
Rearrange again to obtain the more common form:

2a x  vf
2

2  v0
vf
2  2a x

16. Which equation do I use?
 First, decide what model is appropriate
 Is the object moving at constant velocity?
 Or, is it accelerating uniformly?
 Next, decide whether it’s easier to use an algebraic or a
graphical representation.

17. Constant velocity
If you are looking for the velocity,
 use the algebraic form
 or find the slope of the graph (actually the same thing)

v 
x
t

18. Constant velocity
 If you are looking for the displacement,
 use the algebraic form
 or find the area under the curve

x  v t

19. Uniform acceleration
 If you want to find the final velocity,
 use the algebraic form
vf  at  v0
 If you are looking for the acceleration
 rearrange the equation above

 which is the same as finding the slope of a velocity-time
graph

a 
v
t

20. Uniform acceleration
If you want to find the displacement,
 use the algebraic form
 eliminate initial velocity if the object
starts from rest
 Or, find the area under the curve

x  v0t  1
2
at 2

21. If you don’t know the time…
You can solve for Δt using one of the earlier equations,
and then solve for the desired quantity, or
You can use the equation
2  v0
 rearranging it to suit your needs

vf
2  2a x

22. All the equations in one place
constant velocity uniform acceleration
2  v0
vf
2  2ax
x  v t

x  v0t  1
2
at 2

a 
v
t

vf  at v0
v 
x
t
