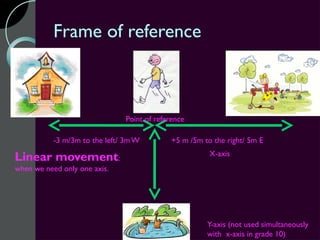
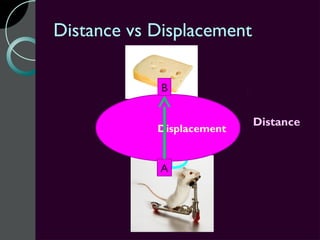
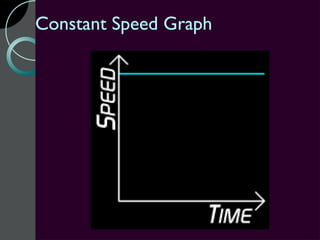
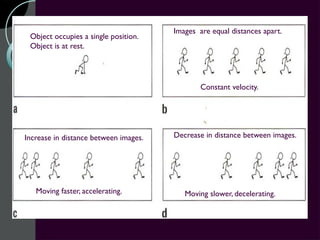
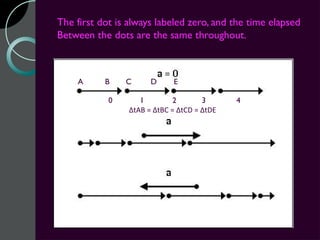
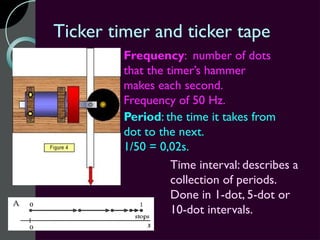
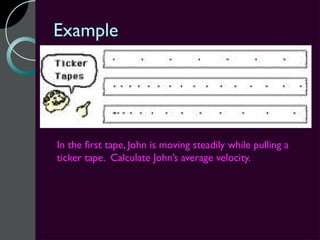
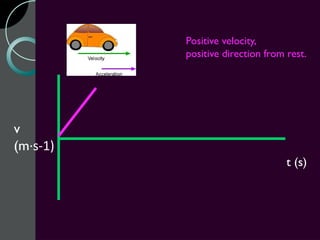
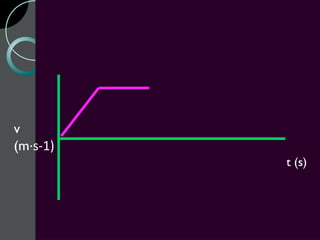
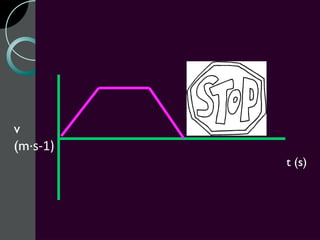
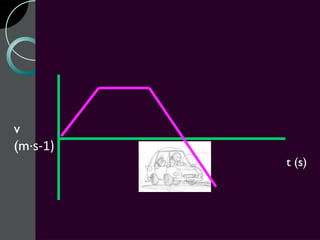
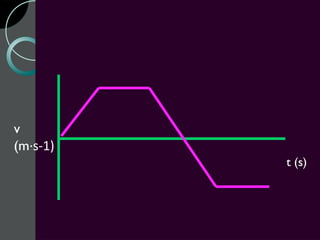
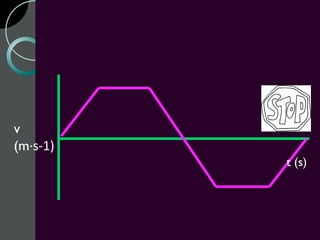
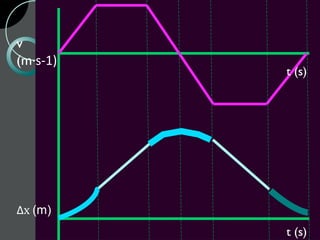
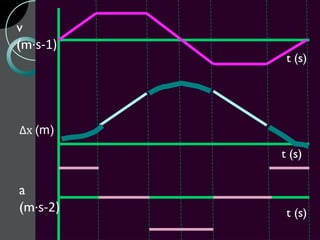
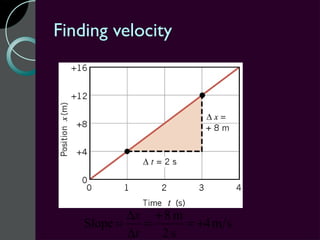
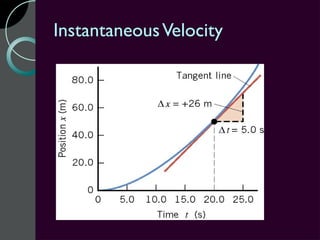
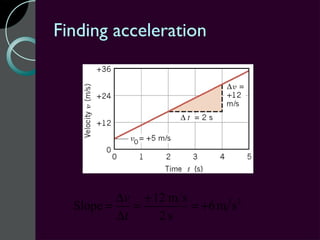
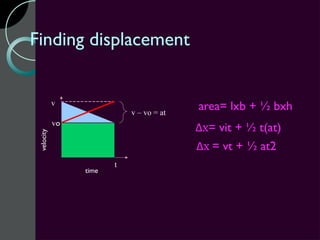
Motion can be described using concepts like position, displacement, distance, speed, velocity, and acceleration. Position refers to an object's location relative to a reference point, while displacement is the change in position. Distance is how far an object moves, while speed is the rate of change of distance over time. Velocity includes both speed and direction of motion. Acceleration describes the rate of change of velocity over time. Motion diagrams, graphs, and equations are used to quantitatively analyze and describe one-dimensional motion.

1. Equations of motion

2. Motion in one dimension

3. What is motion?
Motion is when an object
changes position.
How do you know that
the race car moved?
◦ It changed its position on
the track.

4. How can you tell something has
changed position?
Inorder to see if something has changed position
(motion) you need a reference point.
◦ For example, the starting or finishing line of a racetrack.
Click to edit Master text styles
Second level
Third level
Fourth level
Fifth level

5. Position
Ifsomething moves, it constantly changes
position.
When you describe position, you refer to
a point of reference/origin (zero).
When you have chosen your point of
reference all positions will be chosen
relative to this point of origin.
Position is the place where an object is as
observed from a point of reference.

6. Frame of reference
Point of reference
-3 m/3m to the left/ 3m W +5 m /5m to the right/ 5m E
X-axis
Linear movement:
when we need only one axis.
Y-axis (not used simultaneously
with x-axis in grade 10)

7. GPS
24 satellites
At least 4 sattelites will be visible at any
time from any point
Each sattelite sends a signal to GPS
receivers
The position of the receier can be
determined
Position is given in latitude, longitude and
height

8. Distance and
displacement

9. What is distance?
Easy question!
Distance is how far an object has moved.
We measure distance in METERS!
Distance is the actual path length that is
taken.

10. Distance vs Displacement
B
Distance
Displacement
A

11. What is displacement?
Suppose a runner jogs north to the 50-m
mark and then turns around and runs back
south 30-m.
Total distance is 80-m.
Two directions - north and south.
Displacement is the distance and direction.

12. Displacement
Displacement is the change in position of the
object.
In other words, a straight line.
The magnitude of the displacement will
be smaller than or equal to the distance
that was covered.
Displacement will be represented by Δx
on the horisontal line, and Δy on the
vertical.

13. Calculating distance and displacement
Δx = xf – xi = _m
Let’s try this:
You move from your front porch to your
neighbours’ house 400 m away. Now
calculate your displacement.
Moving from your front door (xi = 0 m ), and
to your neighbours’ house (xf = 400 m).
Δx = xf – xi = 400 – 0 = 400 m to the right

14. Calculating distance and displacement II
Now, you move from your neighbours’ house
and move back towards your house, but move
beyond and travel to the cafe 600 m from your
home. Now calculate your displacement from
the moment you left home.
Moving from your front door (xi = 0 m ), and to
the cafe (xf = 600 m).
Δx = xf – xi = 600 – 0 = 600 m to the left.

15. Scalars and vectors
Scalars
are quantities that has only magnitude.
Examples: distance time mass volume, energy, work and
potential difference
Vectors are quantities that posesses both
magnitude and direction.
Examples: displacement velocity acceleration force weight

16. Speed and velocity

17. What is speed?
Speed is the distance an object travels
over time.
Any change over time is called a RATE.
Speed is the rate at which distance is
traveled.

18. SPEED FORMULA
Speed = Distance / Time
v = Δx / t
Click to edit Master text styles
Second level
Third level
Fourth level
Fifth level

19. Speed Example
 Suppose you ran 2 km in 10 min.
◦ What is your rate?
v = Δx / t
v= 2 km /10 min.
v= 0.2 km/min.
Click to edit Master text styles
Remember the units! Second level
Third level
Fourth level
Fifth level

20. Constant Speed…
What does constant mean?
Ifyou are driving on the highway and you
set your cruise control, you are driving at
a constant speed.
What would a constant speed graph look
like?

21. Constant Speed Graph

22. Do you always go the same speed?
No! Most of the time you are increasing speed,
decreasing speed, or stopping completely!
Think about driving a car or riding a bike!
Click to edit Master text styles
Second level
Third level
Fourth level
Fifth level

23. What would a changing speed graph look
like?

24. What is average speed?
How do you find an average?
Average speed is the total distance
traveled over the total time
v = Δxtotal / ttotal

25. What is Instantaneous speed?
What does a speedometer in a car do?
◦ It shows how fast a car is going at one point
in time or at one instant.
Instantaneous speed is the speed at a
given point in time.

26. What is Velocity?
Speed is how fast something is moving.
Velocity is how fast something is moving
and in what direction it is moving.
Why is this important?
◦ Hurricanes
◦ Airplanes

27. Speed or Velocity?
Ifa car is going around a racetrack, its speed may
be constant (the same), but its velocity is changing
because it is changing direction.
Click to edit Master text styles
Second level
Third level
Fourth level
Fifth level

28. Speed or Velocity?
Escalators have the
same speed (constant),
but have different
velocities because they
are going in different
directions.
Click to edit Master text styles
Second level
Third level
Fourth level
Fifth level

29. acceleration

30. Acceleration
When an object's velocity changes, it
accelerates.
Acceleration shows the change in
velocity during a period of time.
Acceleration = change in velocity /
time
a = Δv/Δt = vf - vi
tf-ti
m·s-2

31. Acceleration II
Magnitude is calculated using the formula.
The direction can be determined as long
as motion is in one dimension.
v = increase, a in the same direction.
v = decrease, a in opposite direction.

32. Positive acceleration
Positive values show that the a
is in the same direction as the
motion. An increase in v.
Negative acceleration
Negative values show that the a
is in the opposite direction from
the motion. A decrease in v.
Constant or uniform acceleration
We only use constant acceleration. Because we
work with constant a, instantaneous and average
acceleration will always be the same. This means
we use the same formula to calculate all three
types of acceleraion.

33. Describing motion with
diagrams

34. What is a motion diagram?
Click to edit Master text styles
◦ Second level
 Third level
 Fourth level
 Fifth level

35. Images are equal distances apart.
Object occupies a single position.
Object is at rest.
Constant velocity.
Increase in distance between images. Decrease in distance between images.
Moving faster, accelerating. Moving slower, decelerating.

36. Sketches and uses
Sketch a row of dots to represent the
object.
Refer to previous slide to get the spaces
right.
Draw a vector from each dot to show
velocity.
If acceleration occurs, add one more
vector to illustrate acceleration.

37. The first dot is always labeled zero, and the time elapsed
Between the dots are the same throughout.
A B C D E
0 1 2 3 4
ΔtAB = ΔtBC = ΔtCD = ΔtDE

38. Ticker timer and ticker tape
Frequency: number of dots
that the timer’s hammer
makes each second.
Frequency of 50 Hz.
Period: the time it takes from
dot to the next.
1/50 = 0,02s.
Time interval: describes a
collection of periods.
Done in 1-dot, 5-dot or
10-dot intervals.

39. Determine the magnitude of the avg
velocity
You will need Δx and Δt for each specific
interval.
Δx = determined by measuring spaces
between intervals.
Δt = determined by multiplying the
spaces with the period.

40. Example
In the first tape, John is moving steadily while pulling a
ticker tape. Calculate John’s average velocity.

41. Determining the avg acceleration
You need four sets of information:
vf, vi, tf and ti
vf – vi = Δv for first interval, and for last
interval.
tf – ti = Δt where time is relative to the
time in the centre of the first and the last
interval.

42. Example
Click to edit Master text styles
◦ Second level
 Third level
 Fourth level
 Fifth level
In the third tape, Sarah walks faster, while pulling
a ticker tape. Calculate Sarah’s average acceleration.

43. Description of motion
using graphs

44. Calculus – the abridged edition
Slope of the line
(derivative)
Displacement Velocity acceleration
Area under the curve
(integral)

45. Movement and velocity

46. Positive velocity,
positive direction from rest.
v
(m·s-1)
t (s)

47. v
(m·s-1)
t (s)

48. v
(m·s-1)
t (s)

49. v
(m·s-1)
t (s)

50. v
(m·s-1)
t (s)

51. v
(m·s-1)
t (s)

52. Position-time graphs for velocity

53. v
(m·s-1)
t (s)
Δx (m)
t (s)

54. Movement with acceleration

55. v
(m·s-1)
t (s)
Δx (m)
t (s)
a
(m·s-2) t (s)

56. Finding velocity
∆x + 8 m
Slope = = = +4 m s
∆t 2s

57. Instantaneous Velocity

58. Finding acceleration
∆v + 12 m s
Slope = = = +6 m s 2
∆t 2s

59. Finding displacement
v
v – vo = at
area= lxb + ½ bxh
vo
Δx= vit + ½ t(at)
velocity
Δx = vt + ½ at2
t
time

60. Equations of motion

61. Symbols
vi = initial velocity in m·s-1
vf = final velocity in m·s-1
a = acceleration in m·s-2
Δx or Δƴ = displacement in m
t = time in s

62. The formulas
vf = vi +aΔt
Δx = viΔt + ½ aΔt2
Δx = (vf2+ vi)Δt
Vf2 = vi2 + 2aΔx

63. Principles
When using v, a and Δx, remember that they are
vectors, so take direction into account. Original
direction of motion = +.
If an object starts from rest, vi = 0 m/s
If an object stops, vf = 0 m/s
If chosen direction is +, then all v, and Δx
substitutions are +.
 If velocity increases, it is +.
If velocity decreases, it is -.
Equations can only be used for motion with constant
acceleration in a straight line.
Work in SI units.