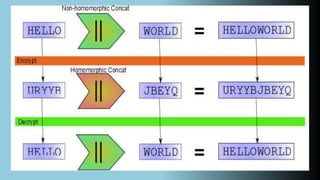
This document provides an overview of homomorphic encryption. It begins by defining homomorphic encryption as a form of encryption that allows specific types of computations to be performed on ciphertext and generate an encrypted result that matches the operations performed on the plaintext when decrypted. It then discusses different types of homomorphic encryption including partially homomorphic (additive or multiplicative), fully homomorphic encryption, and provides examples like RSA, ElGamal, and Paillier. The document concludes by listing some applications of homomorphic encryption such as e-voting, biometric verification, and discusses Paillier encryption specifically.

1. HOMOMORPHIC
ENCRYPTION
By,
Sreelakshmy.R
A Ganga Mythily

2. Private Search
Delegate PROCESSING of data
without giving away ACCESS to it
► You: Encrypt the query, send to Google
(Google does not know the key, cannot “see” the query)
► Google: Encrypted query → Encrypted results
(You decrypt and recover the search results)
2 of 32

3. Private Cloud Computing
Delegate PROCESSING of data
without giving away ACCESS to it
(Input: x) (Program: P)
Enc(x), P → Enc(P(x))
Encrypt x
3 of 32

4. A form of encryption which allows specific types of
computations to be carried out on ciphertext and
generate an encrypted result which, when decrypted,
matches the result of operations performed on the
plaintext.
What is homomorphic encryption?

6. Different types of HE
- Partially Homomorphic - (Additively or Multiplicatively)
- RSA
- ElGamal
- Paillier
- Fully Homomorphic
- Gentry’s System

7. Applications
- E-voting
- Biometric verification
- Protection of mobile agent
- Lottery protocol

8. Electronic Voting- Protecting Data

9. A Symmetric Homomorphic
Encryption Scheme over Integers
Shared key: odd integer p
● To encrypt a bit m:
Choose at random large q, small r (|r| < p/2)
Cipher c = pq + 2r + m [ Ciphertext is close to a multiple of p ]
● To decrypt c:
Message m = (c mod p) mod 2

10. How is it homomorphic?
Homomorphic Addition
c1 = q1p + 2r1 + m1
c2 = q2p + 2r2 + m2
c1 + c2 = (q1 + q2)p + 2(r1 + r2) + (m1 + m2)
c’ = q’p + 2 r’ + m’

11. How is it homomorphic?
Homomorphic Multiplication
c1 = q1p + 2r1 + m1
c2 = q2p + 2r2 + m2
c1 *c2 =(c1q2+q1c2q1q2)p + 2(2r1r2 + r1m2 + m1r2) + m1m2
c’ = q’p + 2 r’ + m’

12. Paillier Encryption
- Pascal Paillier in 1999
- Probabilistic algorithm
- Additively homomorphic system
m = plaintext, c = ciphertext
E(m) is encryption of m, D(c) is decryption of c
D(E(m1) E(m2)) = m1 + m2

13. Thank you