The document explains homomorphic encryption, highlighting its ability to perform operations on encrypted data without decryption, which enhances privacy in various applications such as medical records and spam filtering. It discusses different types of homomorphisms and compares various encryption schemes, emphasizing the importance of selecting an appropriate scheme for specific applications. Practical examples illustrate how homomorphic encryption can facilitate secure computations while maintaining data privacy.




![July 2013:
Change in "De-Mail-Gesetz" defining De-Mail as
secure [1]
● Needs to be decrypted by
provider to "check for viruses"
● (Secret) key on server of provider
○ Server becomes juicy target
● Homomorphic encryption
○ Can check without decryption
[1] http://www.spiegel.de/netzwelt/netzpolitik/de-mail-bundestag-erklaert-bundes-mail-per-gesetz-als-sicher-a-895361.html
Current context
5](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-5-320.jpg)






























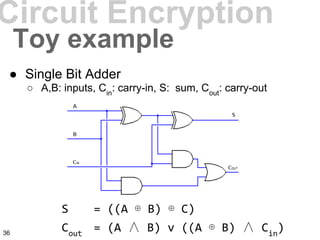






![Encrypted Memory Access
●
row3
= ao
∧ a1
∧ m3
row2
= ¬ao
∧ a1
∧ m2
row1
= ao
∧ ¬a1
∧ m1
row0
= ¬ao
∧ ¬a1
∧ m0
c = row0
∨row1
∨row2
∨row3
[1] M Brenner, J Wiebelitz, G von Voigt. Secret program execution in the cloud applying homomorphic encryption. 201143](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-43-320.jpg)








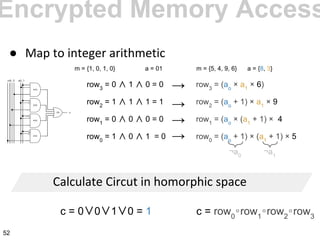






![Gentry's approachGentry's approach
@ł€¶ħæſðđŋæſþðøđł«»¢„
0101100101000101111
@ł€¶ħæſðđŋæſþðøđł«»¢„
³½¬³½¬[¬¼]²′³}³¬½¼¬³²³]
qebrgibfvjkadfnvarskdjhfq
þø»«ĸ@ł½{µ„þøþ@↓ðħþ
plaintext
ciphertext
refreshed ciphertext
ciphertext
secret key
encryption of secret key
59 catechism, flickr (CC BY-NC-SA 2.0)](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-59-320.jpg)

![[...] a simple string search using
homomorphic encryption is about a trillion
times slower than without encryption. [1]
Issues
1 000 000 000 000x
61 [1] CryptDB: A practical encrypted relational DBMS, RA Popa, N Zeldovich, H Balakrishnan, 2011](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-61-320.jpg)

![Fully hom. enc. IRL
● HELib by Shai Halevi (2013)
○ Implementation of Brakerski-Gentry-Vaikuntanathan[1]
scheme
○ Using many optimizations in literature[2][3] for speed
○ Does not implement bootstrapping (yet)
[1] Zvika Brakerski, Craig Gentry, Vinod Vaikuntanathan: (Leveled) fully homomorphic encryption without bootstrapping. ITCS 201
[2] Nigel P. Smart, Frederik Vercauteren: Fully Homomorphic SIMD Operations. IACR Cryptology ePrint Archive 2011: 133 (2011)
[3] Craig Gentry and Shai Halevi and Nigel P. Smart Homomorphic Evaluation of the AES Circuit, CRYPTO 2012
Performance
Modulus Time for addition (ms) Time for multiplication
(ms)
257 0.7 39
8209 0.7 38
65537 2.9 177
Even numbers < 65537,
80 Bits of security
63](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-63-320.jpg)
![Visions of a fully homomorphic cryptosystem
have been dancing in cryptographers' heads for
thirty years. [...] It will be years before a
sufficient number of cryptographers examine
the algorithm that we can have any confidence
that the scheme is secure. [1]
—Bruce Schneier, cryptographer, April 2013
Criticism
“ “
64
[1] Homomorphic Encryption Breakthrough, Schneier on Security, Bruce Schneier https://www.schneier.
com/blog/archives/2009/07/homomorphic_enc.html](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-64-320.jpg)


![Conclusion
— Halevi, 2012
“ “
67
[1] Recent Advances in Homomorphic Encryption, presentation by Shai Halevi, IBM Research, Feb. 13, 2012, http://n
csail.mit.edu/sys-security/FHE.pptx](https://image.slidesharecdn.com/introductiontohomomorphicencryption-130918131259-phpapp01-140319061012-phpapp01/85/Introduction-to-Homomorphic-Encryption-67-320.jpg)

