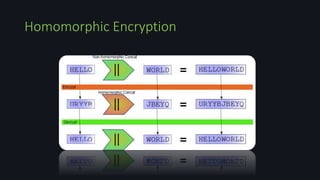
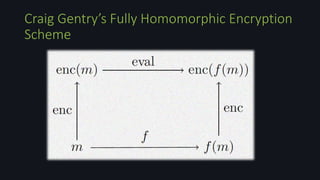
Homomorphic encryption allows computations to be performed on encrypted data without decrypting it first. This document discusses homomorphic encryption techniques including partially homomorphic encryptions that support either addition or multiplication operations, and fully homomorphic encryption introduced by Craig Gentry that supports both types of operations. It also covers the use of ideal lattices in lattice-based cryptosystems and the bootstrapping technique used to "refresh" ciphertexts and prevent noise from accumulating during homomorphic computations.

1. Homomorphic Encryption
Rüstem Göktuğ SEREZ

2. Computations on the Encrypted Data
• The user can be able to make operations his/her encrypted data
without decrypting it.
• The user can also encrypt the queries that send to the encrypted
data.

3. Usage of Homomorphic Encryption
• Secure Voting Systems
• Cloud Security
• Private Information Retrieval (PIR)
• Collision Resistant Hash-Functions
• Hybrid Wireless Network

4. Homomorphic Encryption

5. People currently working on Homomorphic
Encryption
• Craig Gentry, the creator of first homomorphic scheme
• Shai Halevi
• Zvika Brakerski
• Vinod Vaikuntanathan
• Marten van Dijk
• Eleanor Rieffel
• Nigel Smart
• Victor Shoup

6. Cloud Computing
• Compute on encrypted data

7. What is the term ‘Homomorphism’
• In ancient Greek it is translated into the ‘Same Form’
• Subtypes of Homomorphism
• Isomorphism
• Automorphism
• Endomorphism

8. Groups (recall from previous lecture)
• A group is a pair (G,●) consisting of a nonempty set G and a binary
operation ●, (closed) on G, such that (∀ P,Q,R ∈ G)
• Binary operation is associative; (P ● Q) ● R = P ● (Q ● R)
• A unique identity exists; 0 ● P = P ● 0 = P
• Every element has a unique inverse; P ● Q = Q ● P = 0
• Furthermore, (G,+) is abelian if P ● Q = Q ● P ∀ P,Q ∈ G

9. Group Homomorphism
Let (G1 ,●) and (G2 , ●) be groups, and let f : G1 -> G2 be a function. Then
f is said to be a group homomorphism if
f(a ● b) = f(a) ● f(b)
for all a,b in G1.
Every isomorphism is an one-to-one and onto homomorpism.

10. Group Homomorphism
G2G1
a
b
a●b
f(a)
f(b)
f : G1 -> G2
f(a) ● f(b)
f
f
f

11. Homomorphic Encryption
• Fully Homomorphic Encryption
• Partially Homomorphic Encryption

12. Partially Homomorphic Encryptions
• Multipications
• Raw RSA
• ElGamal
• Additions
• Paillier
• Goldwasser-Micali

13. Raw RSA
Encrypt(m) = 𝑚 𝑒 𝑚𝑜𝑑 𝑛
Homomorphic property of RSA is;
• Encrypt(𝑚1) * Encrypt(𝑚2)
= 𝑚1
𝑒 ∗ 𝑚2
𝑒 𝑚𝑜𝑑 𝑛= (𝑚1 ∗ 𝑚2) 𝑒 𝑚𝑜𝑑 𝑛
= Encrypt(𝑚1 ∗ 𝑚2)

14. Raw RSA MAGMA code
p:=NextPrime(Random([1..2^124]));
q:=NextPrime(Random([1..2^124]));
n:=p*q;
phi:=(p-1)*(q-1);
repeat
e:=Random([1..phi]);
until GCD(e,phi) eq 1;
g,x,y:=XGCD(e,phi);
d:=x mod phi;
//ENCRYPTION
m:=Random([0..n]);
c:=Modexp(m,e,n);
m;
//DECRYPTION
Modexp(c,d,n);

15. Partially Homomorphism of Raw RSA MAGMA code
p:=NextPrime(Random([1..2^124]));
q:=NextPrime(Random([1..2^124]));
n:=p*q;
phi:=(p-1)*(q-1);
repeat
e:=Random([1..phi]);
until GCD(e,phi) eq 1;
g,x,y:=XGCD(e,phi);
d:=x mod phi;
//ENCRYPTION
m1:=Random([0..n]);
m2:=10;
c:=Modexp(m1*m2,e,n);
(Modexp(m1,e,n)*Modexp(m2,e,n)) mod n;
c;
//DECRYPTION
Modexp(c,d,n);
(m1*m2) mod n;

16. ElGamal
Encrypt(M) =𝑃 𝑟, 𝑀 ∗ 𝑄 𝑟
Homomorphic property of ElGamal is;
• Encrypt(𝑀1) * Encrypt(𝑀2)
= 𝑃 𝑟1+𝑟2, (𝑀1*𝑀2)*𝑄 𝑟1+𝑟2
= Encrypt(𝑀1 ∗ 𝑀2)

17. ElGamal MAGMA code
G := IntegerRing(558494556463);
P := G!197214177966;
k := Random(#G);
Q := P^k;
//ENCRYPTION
M := G!37498469442;
M;
r := Random(#G);
C0 := P^r; //C0 := r*P
C1 := M*(Q^r); //C1 := M+r*Q
//DECRYPTION
C1/C0^k; //C1-k*C0

18. Partially Homomorphism of ElGamal MAGMA code
G := IntegerRing(558494556463);
P := G!197214177966;
k := Random(#G);
Q := P^k;
//ENCRYPTION
M1 := G!37498469442;
M2 := G!48494459451;
r1 := Random(#G);
r2 := Random(#G);
C00 := P^r1; //C00 := r1*P
C10 := M1*(Q^r1); //C10 := M1+r1*Q
C01 := P^r2; //C01 := r2*P
C11 := M2*(Q^r2); //C11 := M2+r2*Q
Ca := P^(r1+r2); //Ca := P*(r1+r2)
Cb := M1*M2*(Q^(r1+r2)); //Cb := (M1 + M2)+Q*(r1+r2)
C00 * C01;
C10 * C11;
Ca;
Cb;
//DECRYPTION
Cb/Ca^k;
M1*M2;

19. Paillier
• Encrypt(m) = 𝑔 𝑚 𝑟 𝑛 𝑚𝑜𝑑 𝑛2
Homomorphic property of Paillier is;
• Encrypt(𝑚1) * Encrypt(𝑚2)
= (𝑔 𝑚1 𝑟1
𝑛)* (𝑔 𝑚2 𝑟2
𝑛)
= 𝑔 𝑚1+𝑚2 ∗ (𝑟1 𝑟2) 𝑛
= Encrypt((𝑚1 + 𝑚2) 𝑚𝑜𝑑 𝑛2
)

20. Fully Homomorphic Encryption
Plaintext and Ciphertext are both in 𝑧2 ring
Function E in homomorphic for both addition and multipication if;
E(x) + E(y) = E(x + y)
E(x) * E(y) = E(x * y)

21. Fully Homomorphic Encryption
• Is there an encryption function (E) such that both E(x + y) and E(x.y)
are easy to compute from E(x) and E(y)? (Rivest 1978)

22. What is ‘Fully Homomorphic’?
• Function ‘Evaluate’ must output a ciphertext which can be efficiently
computed without any loss.

23. Craig Gentry’s Fully Homomorphic Encryption
Scheme
An additional ‘Evaluate’ function on encrypted data.
𝐶∗ ← Evaluate (pk, C, 𝐶∗
1, . . . , 𝐶∗
𝑡)

24. Craig Gentry’s Fully Homomorphic Encryption
Scheme

25. Craig Gentry’s Fully Homomorphic Encryption
Scheme
• Somewhat Homomorphic Encryption
• Bootstrapping

26. Noise Parameter
• The multipication and addition is done by
attached «noise parameter» in ciphertext
which is smaller than N.

27. Somewhat Homomorphism
• Encryption outputs a ciphertext with small noise less than n.
• But, decryption works as long as the noise is less than some threshold
N ≫ n.
• Depth of circuits roughly is; log log N − log log n

28. Suppose we have ‘Recrypt’ function which has;
• Input: ciphertext E(a) with noise 𝑁′ < 𝑁 .
• Output: «fresh» ciphertext E(a) with noise 𝑁′′ < 𝑁.
(Also encrypts ‘a’ again)
This operation is done recursively.
Then, we can constract a fully homomorphic scheme for ‘Recrypt’
function out of somewhat homomorphic scheme for addition and
multipication.
The term ‘Fully Homomorphic’

29. Somewhat Homomorphic Scheme Example
using Integers
• KeyGen = Odd(p) > 2N
• Plaintext is b = {0,1}
• x = Random(-n/2, n/2)
• k ∈ ℤ
• Ciphertext is c = b + 2x + k*p which b + 2x ∈ −𝑁, 𝑁 ⊂ (−p/2, p/2)
• Noise is c mod p
• Decryption is b = (Noise) mod 2

30. Somewhat Homomorphic Scheme
• To add two ciphertexts;
𝑐 = 𝑐1 + 𝑐2 = 𝑏1 + 𝑏2 + 2 𝑥1 + 𝑥2 + 𝑘1 + 𝑘2 𝑝 = 𝑏1⨁ 𝑏2 + 2𝑥 + 𝑘𝑝
Decryption recovers the 𝑏1⨁ 𝑏2 as long as (𝑏1 + 2𝑥1) + (𝑏2 + 2𝑥2) ∈ [-N,N]
• To multiplicate two ciphertexts;
𝑐 = 𝑐1 ∗ 𝑐2 = 𝑏1 ∗ 𝑏2 + 2 𝑏1 𝑥2 + 𝑏2 𝑥1 + 2𝑥1 𝑥2 + 𝑘𝑝 = 𝑏1 ∗ 𝑏2 + 2x +𝑘𝑝
Decryption recovers the 𝑏1 ∗ 𝑏2 as long as (𝑏1 + 2𝑥1) * (𝑏2 + 2𝑥2) ∈ [-N,N]

31. Lattice Based Cryptosystems
• Cryptosystems based on computational hardness of several lattice
problems which are;
• Shortest Vector Problem (SVP)
• Closest Vector Problem (CVP)
• Shortest Independent Vector Problem (SIVP)
• Bounded Distance Decoding Problem (BDDP)
• Ideal Coset Problem (ICP)

32. Rings and Ideals
• A ring is a set which are closed under addition, multiplication and
have an addivite identitiy ‘0’ and multiplicative identitiy ‘1’
• An ideal I of a ring R is a subset 𝐼 ⊆ 𝑅 such that 𝑗=1
𝑡
𝑖𝑗 ∗ 𝑟𝑗 ∈ 𝐼 for
any 𝑖1, … , 𝑖 𝑡 ∈ 𝐼 and 𝑟, … , 𝑟𝑡 ∈ 𝑅
E.g. 2 is an ideal of ℤ consisting of the set of even numbers.

33. • An ideal lattice, is simply an ideal in ℤ[x]/(f(x)).
• f(x) of degree n; each such ideal can be represented by a lattice
generated by the columns of a lattice basis 𝐵𝚤 , an n × n matrix.
Ideal Lattices

34. Ideal Lattices
• Ideal lattices gives the public key scheme of the somewhat
homomorhpic encryption.
• «Good» representation of an ideal lattice can be used as secret key.
• «Bad» representation of an ideal lattice can be used as public key.
• Where is the security of it?

35. Ideal Coset Problem (ICP)
This problem is close to the decision problem of Closest Vector
Problem.
R is a ring,
I and J are relatively prime ideals if I + J = R.
𝐵𝚤 is the basis of the given lattice L
Fix R, 𝐵𝚤, algorithm IdealGen, and an algorithm Samp1 that efficiently
samples R.

36. The challenger sets b ← 𝑅
{0, 1} and (𝐵J
sk 𝐵J
pk
) ← 𝑅
IdealGen(R, 𝐵𝚤).
If b = 0, it sets r ← 𝑅
Samp1(R) and t ← r mod 𝐵J
pk
.
If b = 1, it samples t uniformly from R mod 𝐵J
pk
.
The problem: guess b given (t, 𝐵J
pk
).
Ideal Coset Problem (ICP)

37. Subset Sum problem
Gives security against recovering secret key from additional data due to
squashing the decryption circuit.

38. • Let J is an ideal lattice in ring R
• j ∈ J
• Plaintext is b = {0,1}
• x = Random(-n/2, n/2)
• k ∈ ℤ
• Ciphertext is c = b + 2x + J which b + 2x ∈ −𝑁, 𝑁 ⊂ (−p/2, p/2)
• Decryption is b = (Noise) mod 2
Back to Somewhat Homomorphic Scheme

39. Noise Problem
• While addition and multipication operations are being occured, the
«noise» increases.
• If «noise» ∉ −𝑛, 𝑛 then decryption will be wrong.
• An extra operation needed for «refreshing» the cyphertext if the
secret key is unknown.

40. • A self-sustaining process without requiring any external help.
Bootstrapping

41. Bootstrapping
• The noise parameter increases every computation on encrypted data.
• A «Refresh» is needed for the ciphertext every once in a while.

42. • If the bootstrapping can be made, than we can refresh ciphertext via
recryption.
• Suppose we have two public-secret key pairs;
• (𝑠𝑘1, 𝑝𝑘1) = (𝑠𝑘2, 𝑝𝑘2)
• Then;
• Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘1, Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘1,m)) = m
• Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘2, Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘2,m)) = m
for any message.
Bootstrapping

43. • Take an encryption of 𝑠𝑘1 under the public key 𝑝𝑘2
• Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘2, 𝑠𝑘1) = 𝐸1
• Take an encryption of the initial ciphertext under the public key pk2
• Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘2, Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘1,m)) = 𝐸2
Bootstrapping

44. • Consider;
• Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝐸1,𝐸2) = Encrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑝𝑘2,m)
The inner encryption is removed
• Assume the scheme «Evaluate» can homomorphically evaluate;
• Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘,𝑐1) + Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘,𝑐2)
• Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘,𝑐1) * Decrypt 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒(𝑠𝑘,𝑐2)
Then the «Evaluate» is bootstrappable
Bootstrapping

45. Advantages of using Ideal Lattices
• Very low circuit complexity compared to RSA or ElGamal.
• Security can be based on standard problems over ideal lattices, that
seem to be as hard as standard well-studied problems over general
lattices.

46. Inefficiency of Craig Gentry ’s scheme
• Computation time increases sharply with the security level of the
homomorphic scheme.
• The computation time and ciphertext size in Craig Gentry’s scheme
are high-degree polynomials.
• Decryption circuit depth is larger than what EvaluateE function can
handle.

47. Second Homomorphic Encryption Scheme
An additional secret key is added into ciphertext scheme,
c * s = b + 2e
Security is based on the hardness of Learning with Errors problem.
• Improved noise behavior
• Improved security reductions
• Significant efficiency improvements using “batching”

48. Implementations
• Using Homomorphic Encryption for Large Scale Statistical Analysis
• Private Database Queries using Somewhat Homomorphic Encryption
• HElib library, the implementation of Brakerski-Gentry-
Vaikuntanathan (BGV) scheme focusing;
• Effective use of the Smart-Vercauteren ciphertext packing techniques
• Gentry-Halevi-Smart optimizations

49. HElib
https://github.com/shaih/HElib
• Has been developed in C++ and NTL Number Theory math library by
Victor Shoup and Shai Halevi
• Provides low level operations for multipication, addition etc.
• Suppors multi-threading

50. Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA
//SOMEWHAT HOMOMORPHIC ENCRYPTION using RSA
//
//
//Rüstem Göktuğ SEREZ
//
//
//Referenced by
//Computing Arbitrary Functions of Encrypted Data, Craig
Gentry
//http://crypto.stanford.edu/craig/easy-fhe.pdf

51. //lambda is the security parameter
init := function(lambda)
l := lambda;
N := 2^lambda;
P := 2^(lambda^2);
Q := 2^(lambda^5);
return l,N,P,Q;
end function;
l,N,P,Q := init(3);
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

52. //randomly select odd number of P bits with base 2
keygen := function()
p := Random([1,P-1]);
if (p mod 2) eq 0 then
p := p + Random([1,2]);
end if;
return p;
end function;
p := keygen();
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

53. //compute m' = m mod 2, c = m' + pq
encrypt := function(m)
mprime := Random([1,N-1]);
mprime := mprime - mprime mod 2 + m mod 2;
q := Random([1,Q-1]);
return mprime + p*q;
end function;
//compute m = (c mod p) mod 2
decrypt := function(c)
return (c mod p) mod 2;
end function;
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

54. //RSA
p1:=NextPrime(Random([1..2^124]));
q1:=NextPrime(Random([1..2^124]));
n1:=p1*q1;
phi:=(p1-1)*(q1-1);
repeat
e:=Random([1..phi]);
until GCD(e,phi) eq 1;
g,x,y:=XGCD(e,phi);
d:=x mod phi;
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

55. //RSA ENCRYPTION
m1:=Random([1..n1]);
c1:=Modexp(m1,e,n1);
printf "Plaintext: %on",m1;
printf "Ciphertext: %on",c1;
//value that we will add to ciphertext
op := 128;
//binary conversions
mbin := IntegerToSequence(m1,2);
opbin := IntegerToSequence(op,2);
cbin := IntegerToSequence(c1,2);
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

56. //noise parameter must be smaller than b
//HOMOMORPHIC ENCRYPTION
for i in [1..#opbin] do
cbin[i] := encrypt(cbin[i]) + encrypt(opbin[i]);
end for;
//HOMOMORPHIC DECRYPTION
for i in [1..#cbin] do
cbin[i] := decrypt(cbin[i]);
end for;
//decimal conversion
c2 := SequenceToInteger(cbin,2);
printf "Summed Ciphertext: %on",c2;
printf "Addend value to Ciphertext: %on",AbsoluteValue(c2 - c1);
printf "Noise: %o",c2 mod 2;
Implementation of Somewhat Homomorphic
Encryption over Integers on MAGMA

57. References
• http://blog.cryptographyengineering.com/2012/01/very-casual-introduction-to-fully.html
• http://en.wikipedia.org/wiki/Homomorphic_encryption
• http://en.wikipedia.org/wiki/Homomorphism
• https://github.com/shaih/HElib
• https://martinralbrecht.wordpress.com/2010/08/19/somewhat-homomorphic-encryption/
• http://crypto.stanford.edu/craig/easy-fhe.pdf
• C. Gentry, A FULLY HOMOMORPHIC ENCRYPTION SCHEME, September 2009
• Homomorphic Encryption and Applications, By Xun Yi, Russell Paulet, Elisa Bertino.
• Homomorphic Cryptosystems, Edlyn Teske-Wilson, University of Waterloo, University of Waterloo
• 5 years of FHE, Zvika Brakerski, Weizmann Institute of Science, Aarhus MPC Workshop, May 2014
• Open problems in lattice-based cryptography, Steven Galbraith
• Public Key Ciphers, Hüseyin HIŞIL, Spring, 2014-2015
• Homomorphic Encryption, Shai Halevi, Crypto 2011

58. Thank you for listening