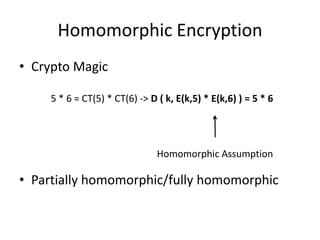
Homomorphic encryption allows computations to be carried out on encrypted data without decrypting it first. This summary discusses Craig Gentry's scheme for fully homomorphic encryption based on ideal lattices. The scheme works by encrypting bits as ciphertexts with small noise that grows with computations. A bootstrapping procedure called re-crypt reduces the noise to keep ciphertexts decryptable. While promising for applications like cloud computing, the scheme has high computational costs that scale poorly with security level. Current research aims to make homomorphic encryption more efficient and practical.

1. Homomorphic Encryption
Craig Gentry scheme

2. Why homomorphic encryption?
• Proposed by Rivest, Adleman and Dertouzos
• Confidentiality problems
• Ability to compute over ciphertext instead of
plaintext
• One could use information without knowing the
content of that information
• Privacy garanteed

3. Homomorphic Encryption
• Crypto Magic
5 * 6 = CT(5) * CT(6) -> D ( k, E(k,5) * E(k,6) ) = 5 * 6
Homomorphic Assumption
• Partially homomorphic/fully homomorphic

4. Homomorphic Encryption
• Partially homomorphic schemes
– RSA: CT(x)*CT(y) = (xe mod M) * (ye mod M) = xeye
mod M = (xy)e mod M = CT(x*y), where e is the
exponent key and M the modulus
• p=61;
• q=53;
• N=3233;
• Φ(N)=60*52=3120;
• e=17;
• d=2753;

5. Homomorphic Encryption
• Partially homomorphic schemes
– RSA: Obtain 5*6 performing RSA(5)*RSA(6)
• RSA(5) = 517 (mod 3233) = 3086;
• RSA(6) = 617 (mod 3233) = 824;
• 3068*824 = 2542864;
• RSA-1(2542864) = 25428642753 (mod 3233) = 30;
• 5*6 = 30;

6. Homomorphic Encryption
• Fully homomorphic schemes
– Craig Gentry scheme
• Based on ideal lattices
– Zaryab Khan scheme
• Based on perfectly colorblind function

7. Craig Gentry scheme
• Suppose a scheme with a “noise parameter”
attached to each CT;
• Encryption algorithm outputs a CT with a small noise
parameter (say less than n);
• Decryption algorithm only works if noise is less than
some parameter N >> n;
• To compute E(a+b) / E(a*b), include noise;
• This gives a “somewhat homomorphic” scheme.

8. Craig Gentry scheme
• Now suppose a new algorithm RECRYPT, such that:
– Input: E(a), with noise N’ < N
– Output: E’(a), with noise √N
• “Somewhat homomorphic” -> fully homomorphic!
• Apply RECRYPT to E(a) and E(b) to ensure that the
noise in E(a*b) or E(a+b) is smaller than N
• “Bootstrappable”

9. Craig Gentry scheme (integers)
• Key: odd integer p > 2N
• Encryption algorithm: given a bit b -> E(b) = c = b +
2x + kp, where x is in [-n/2,n/2] and k is an integer
chosen from some range
• Decryption algorithm: b = (c mod p) mod 2, where (c
mod p) is the noise and belongs to [-n,n]
• Decryption works if b + 2x ∈ [-N,N] ⊂[-p/2,p/2]

10. Craig Gentry scheme (integers)
• Graig Gentry scheme’s homomorphic assumptions
– Addiction: c1 + c2 = b1+ b2 + 2(x1+x2) + (k1+k2)p =
b1 xor b2 + 2x + kp
• Decryption works if (b1+2x1) + (b2+2x2) is in [-
N,N]
– Multiplication: c1*c2 = b1*b2 + 2(b1x2 + b2x1 +
2x1x2) + kp = b1*b2 + 2x + kp
• Decryption works if (b1+2x1) * (b2+2x2) is in [-
N,N]

11. Craig Gentry scheme (integers)
• Addition example: 4+4
– CT(100):
22 21 21
• CT(1) = 1 + 2*3 + 5*3 = 22
+22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21
44 42 42
• CT(0) = 0 + 2*3 + 5*3 = 21
– D(44 42 42):
• D(44) = 44 mod 3 = 2
• D(42) = 42 mod 3 = 0
1000 = 8 = 4+4
• D(42) = 42 mod 3 = 0

12. Craig Gentry scheme (integers)
• Multiplication example: 4*4
– CT(100):
• CT(1) = 1 + 2*3 + 5*3 = 22
22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21 ×22 21 21
• CT(0) = 0 + 2*3 + 5*3 = 21 484 924 1365 882 441
– D(484 924 1365 882 441):
• D(484) = 484 mod 3 = 1
• D(924) = 924 mod 3 = 0
• D(1365) = 1365 mod 3 = 0
10000 = 16 = 4*4
• D(882) = 882 mod 3 = 0
• D(441) = 441 mod 3 = 0

13. Craig Gentry scheme (ideal lattices)
• Replace integers by ideal lattices
• Ideal lattices have many representations or
“bases”
• Bases:
– Good: good to decrypt, bad to encrypt
– Bad: bad to decrypt, good to encrypt
• Public key scheme, where good bases are
private keys and bad bases are public keys

14. Cryptography over lattices
• L = ζ(B) = {Bc : c ∈ Zk}, B ∈ Rn×k, where the k
columns of the basis are linearly independent
• NP-hard problems over lattices:
– SVP (shortest vector problem): given a basis for
lattice L of size n, find the shortest nonzero vector
v ∈ L s.t. ||v|| = λ(L);
– CVP (closest vector problem): given a basis for
lattice L of size n and a vector t ∈ Rn, find a
nonzero vector v ∈ L s.t. ||t-v|| ≤ γ;

15. Cryptography over lattices
• NP-hard problems over lattices:
– SIVP (shortest independent vector problem): like
the SVP, except the output are linearly
independent vectors v1, …, v2 ∈ L of length at
most λ(L);
– BDDP (bounded distance decoding problem):
same as CVP but with the promise that there is a
unique solution.

16. Craig Gentry scheme
• Why inefficient?
– CT size and computation time increase sharply as
the security level increases;
– 2k security -> CT size and computation time are
high-degree polynomials in k;
– Efforts are being made to reduce the
computational requirements of Craig Gentry
construction

17. Homomorphic Encryption
• Nowadays:
– Craig Gentry presented a working implementation
of the fully homomorphic system, including the
bootstrapping function
– Exists a practical application of homomorphic
encryption to a hybrid wireless network
– Perform statistical tests over encrypted data such
as temperature, humidity, etc.
– There are also some practical implementations of
simplifications of this scheme over databases

18. Problems solved
• Cloud security
• Problems related to personal records like
medical records
• Work with information stored in databases
• Querys to search engines
• …

19. My Project
• Design an API and include it on a Web Service
that will work over CLOUD platforms
• The API should provide homomorphic
encryption functions to be used
• Create a prototype that will work under the
constructed API

20. QUESTIONS?