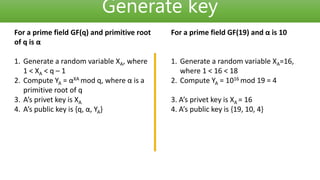
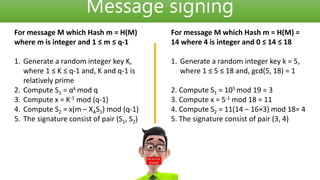
The ElGamal digital signature scheme was described by Tahir Elgamal in 1985. It uses a key pair consisting of a public key and private key, where the private key is used to generate signatures and the public key is used to verify signatures. Signatures provide message authentication, integrity, and non-repudiation by proving the message was signed by the private key holder. The document then proceeds to describe the technical process of generating keys, signing messages, and verifying signatures using ElGamal signatures with an example.

1. ElGamal signature scheme
Welcome
Md.Kawsar Ahmed
Department of Information and Communication
engineering
Pabna University of Science and Technology

2. Teacher CR Student
A story back in 1985

3. ElGamal signature scheme
The ElGamal digital signature scheme was described by Tahir Elgamal in 1985.
• The algorithm uses a key pair consisting of a public key and a private
key.
• The private key is used to generate a digital signature for a message,
and such a signature can be verified by using the signer's
corresponding public key.
• The digital signature provides message
 Authentication (the receiver can verify the origin of the message),
 Integrity (the receiver can verify that the message has not been modified since it was signed)
 Non-repudiation (the sender cannot falsely claim that they have not signed the message).

4. Arithmetic
3
Public Key
2
Privet Key
1
- Randomly
choice-
-
Calculate from
Privet key
-
-
Modulo Arithmetic
-
- Roll 160641 –
- Primitive Root -
- Roll 160621 -
Background Knowledge

5. Generate key
For a prime field GF(q) and primitive root
of q is α
1. Generate a random variable XA, where
1 < XA < q – 1
2. Compute YA = αXA mod q, where α is a
primitive root of q
3. A’s privet key is XA
4. A’s public key is {q, α, YA}
For a prime field GF(19) and α is 10
1. Generate a random variable XA=16,
where 1 < 16 < 18
2. Compute YA = 1016 mod 19 = 4
3. A’s privet key is XA = 16
4. A’s public key is {19, 10, 4}

6. Message signing
For message M which Hash m = H(M)
where m is integer and 1 ≤ m ≤ q-1
1. Generate a random integer key K,
where 1 ≤ K ≤ q-1 and, K and q-1 is
relatively prime
2. Compute S1 = αk mod q
3. Compute x = K-1 mod (q-1)
4. Compute S2 = x(m – XAS1) mod (q-1)
5. The signature consist of pair (S1, S2)
For message M which Hash m = H(M) =
14 where 4 is integer and 0 ≤ 14 ≤ 18
1. Generate a random integer key k = 5,
where 1 ≤ 5 ≤ 18 and, gcd(5, 18) = 1
2. Compute S1 = 105 mod 19 = 3
3. Compute x = 5-1 mod 18 = 11
4. Compute S2 = 11(14 – 16×3) mod 18= 4
5. The signature consist of pair (3, 4)

7. Verify Signature
For verifying a digital signature we have
sender public key {q, α, YA} , message M
which Hash is m and signature (S1, S2)
1. Compute V1 = αm mod q
2. Compute V2 = (𝑌𝐴) 𝑆1(𝑆1) 𝑆2 𝑚𝑜𝑑 𝑞
For verifying a digital signature we have
sender public key {19, 10, 4}, message M
which Hash is 14 and signature (3, 4)
1. Compute V1 = 1014 mod 19 = 16
2. Compute V2 = (4)3(3)4 𝑚𝑜𝑑 19 = 16
3. If V1 = V2, The signature is valid