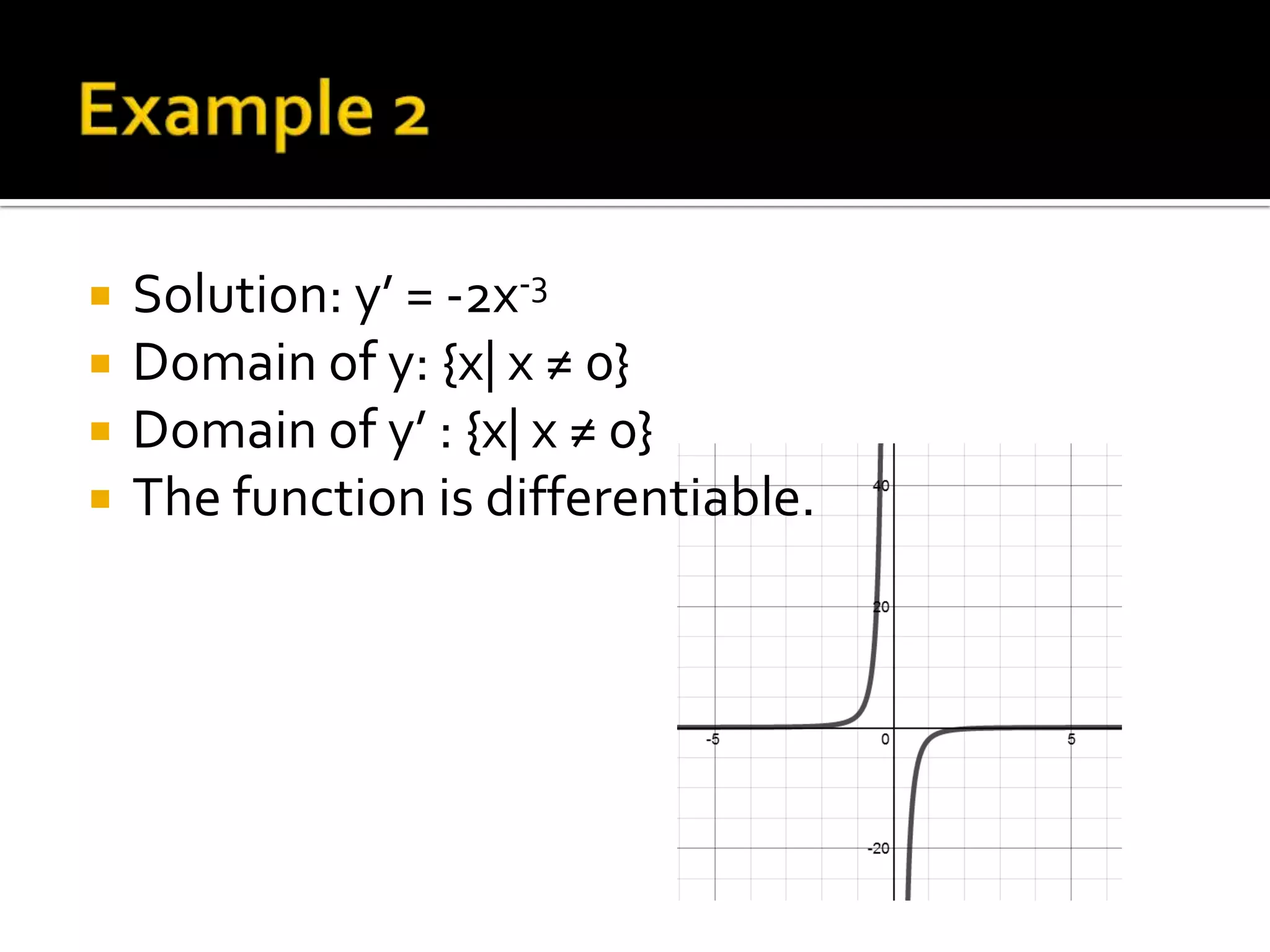
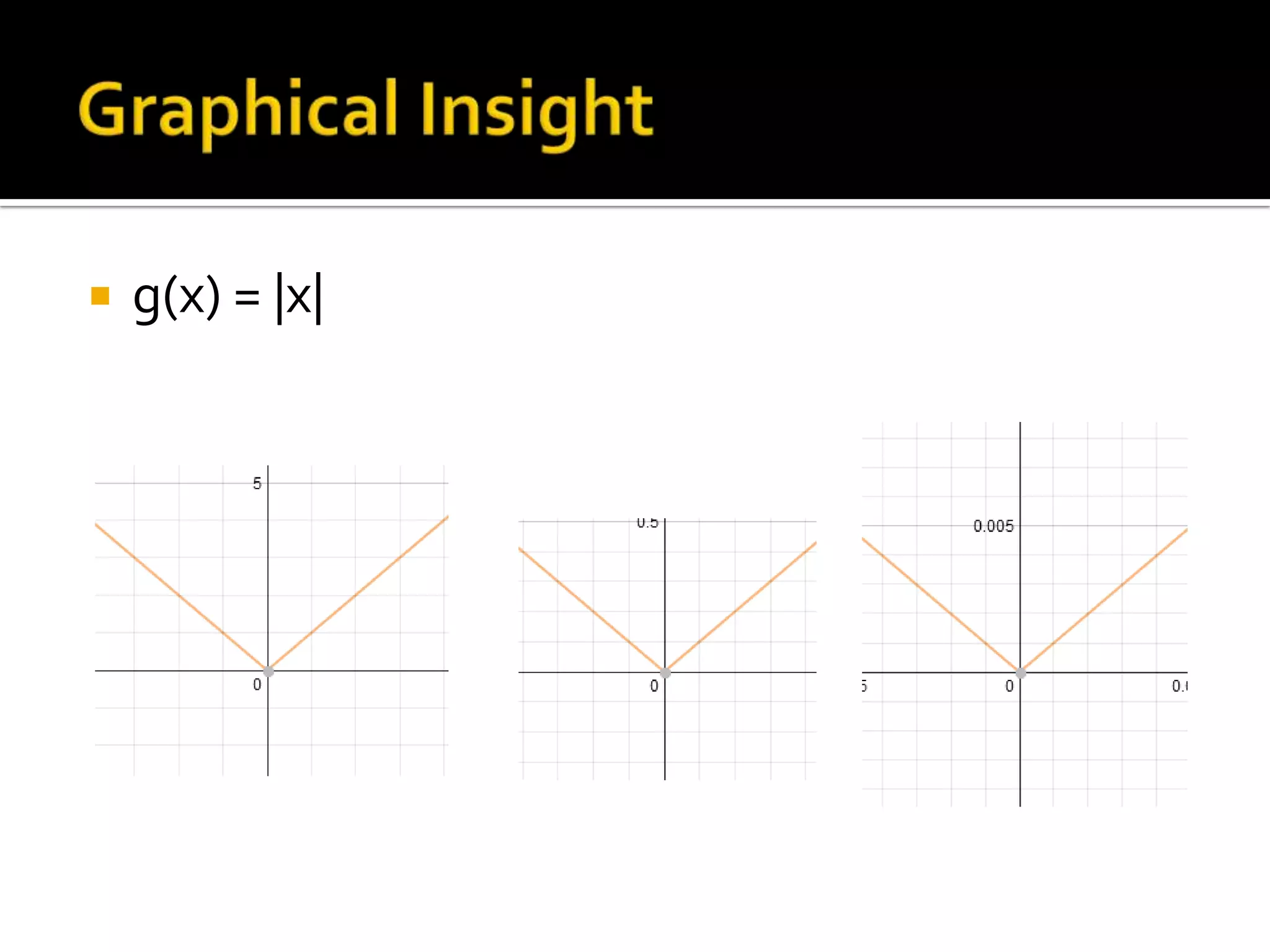
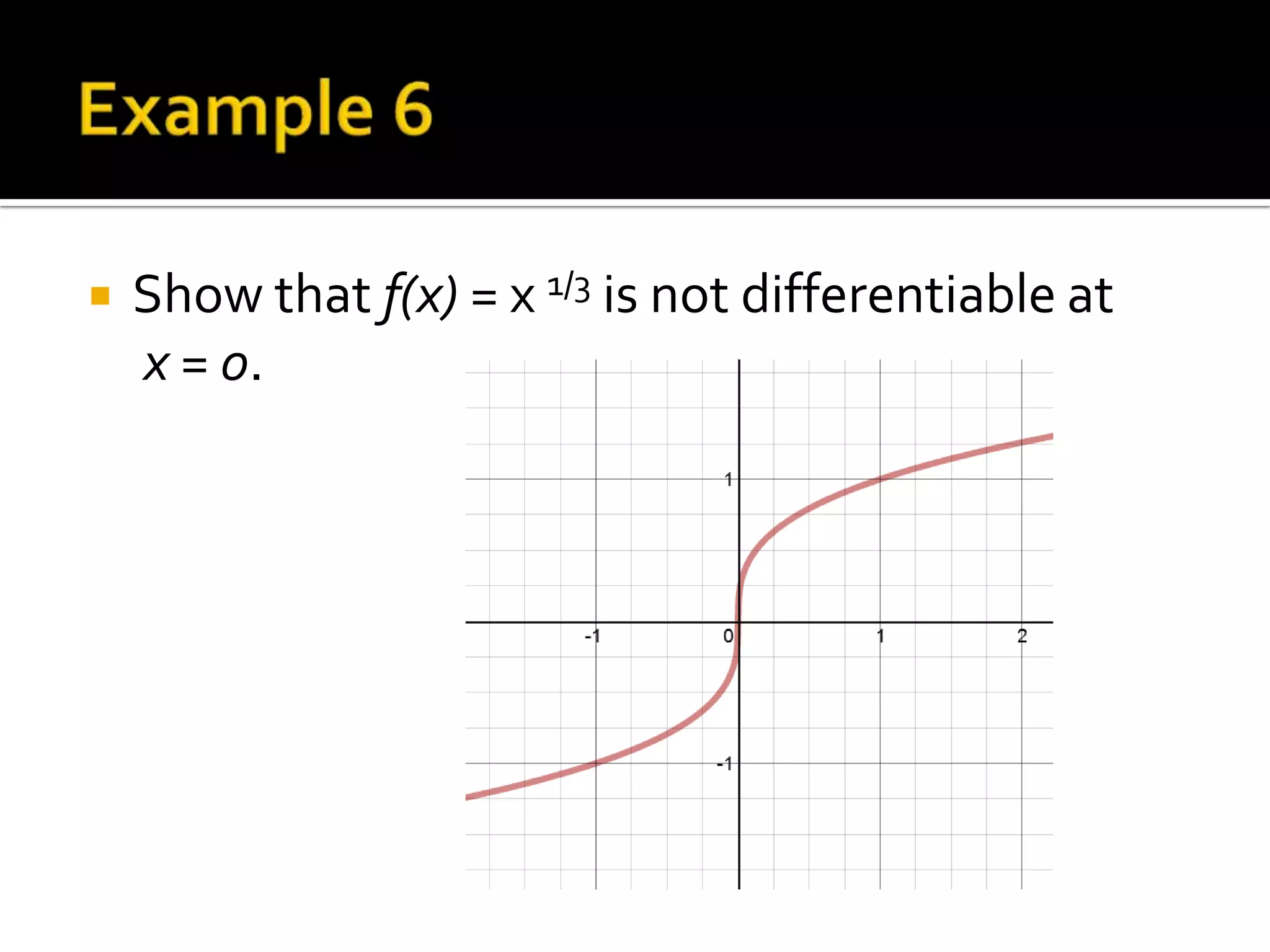
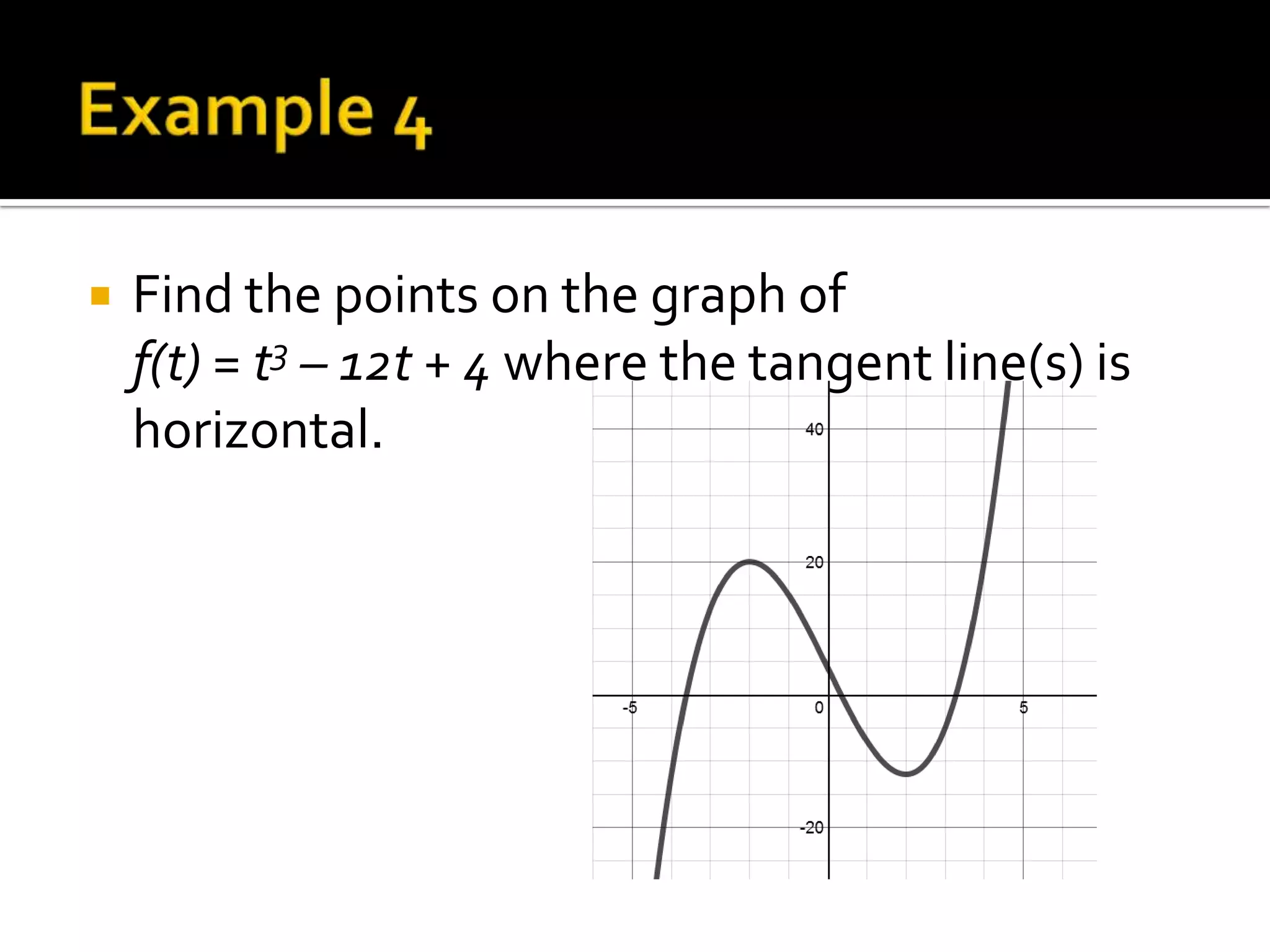
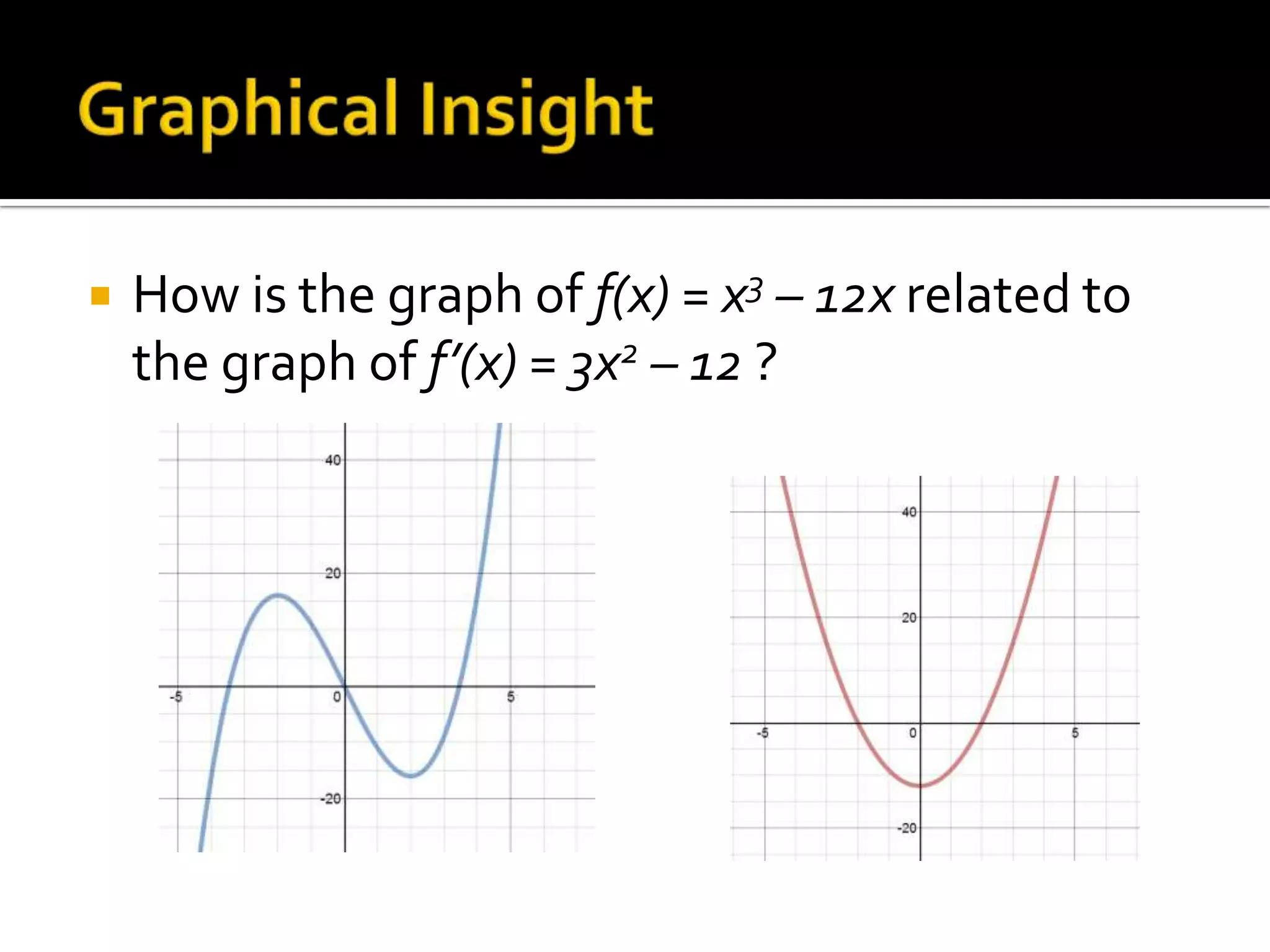
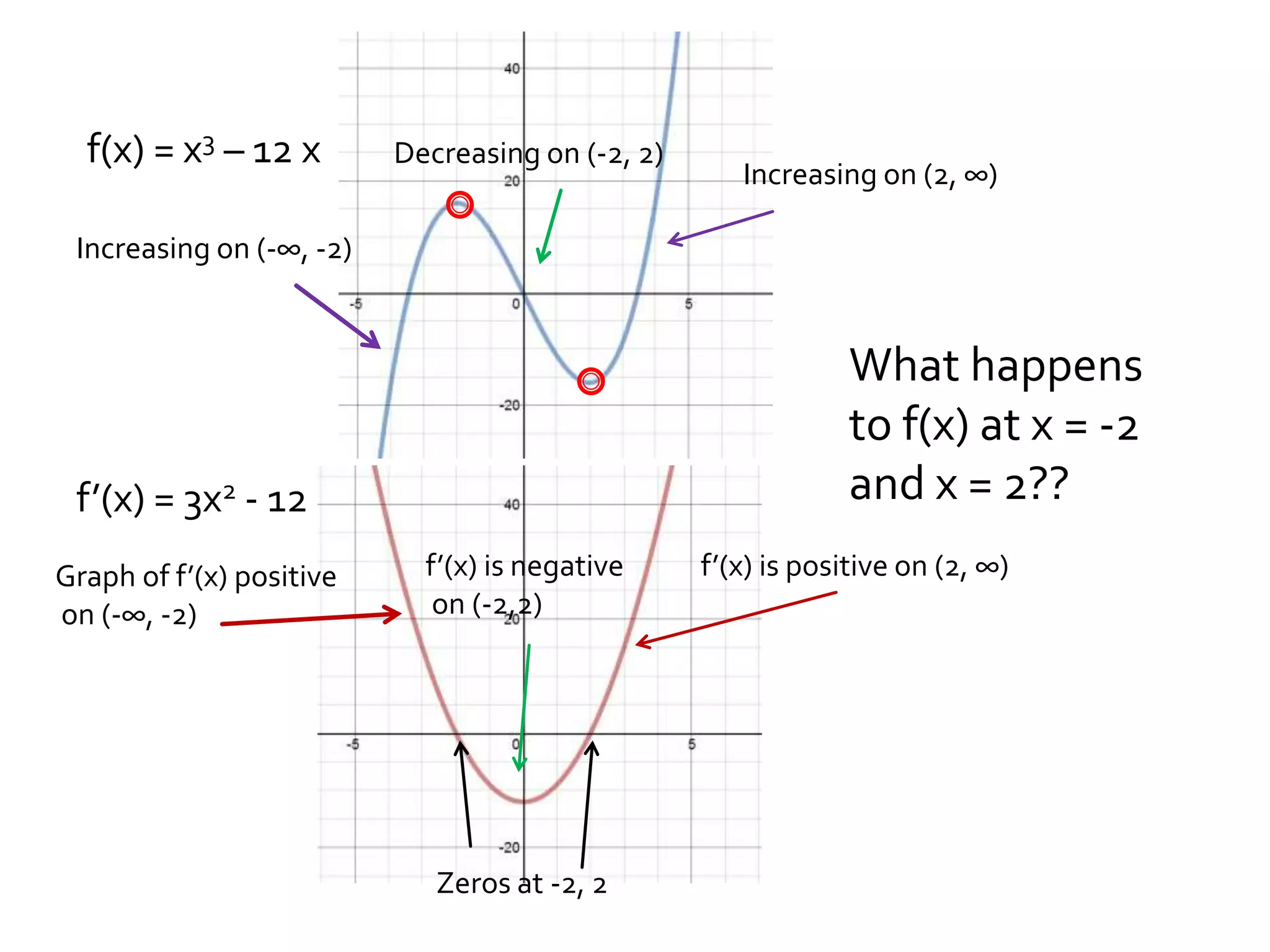
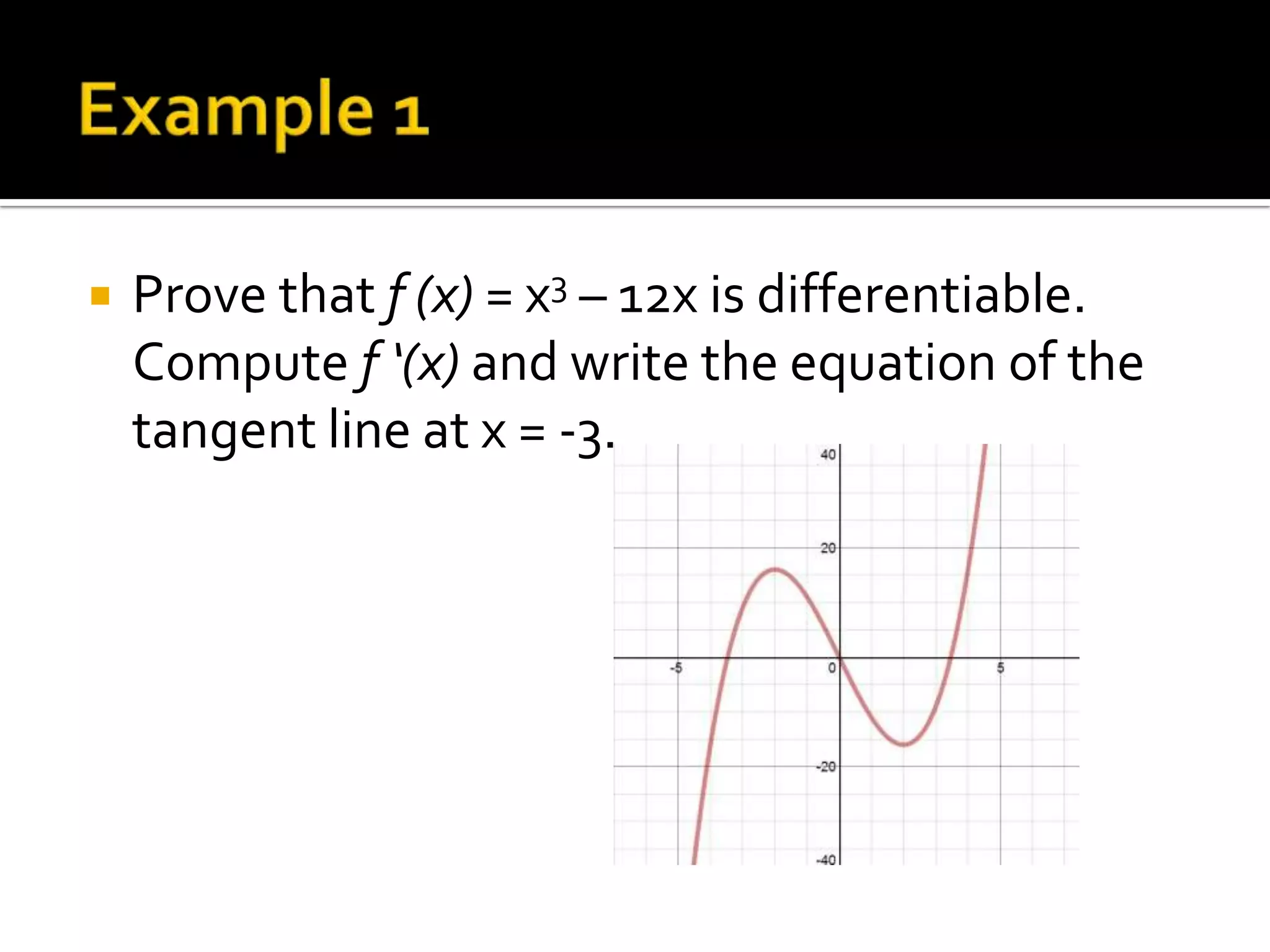
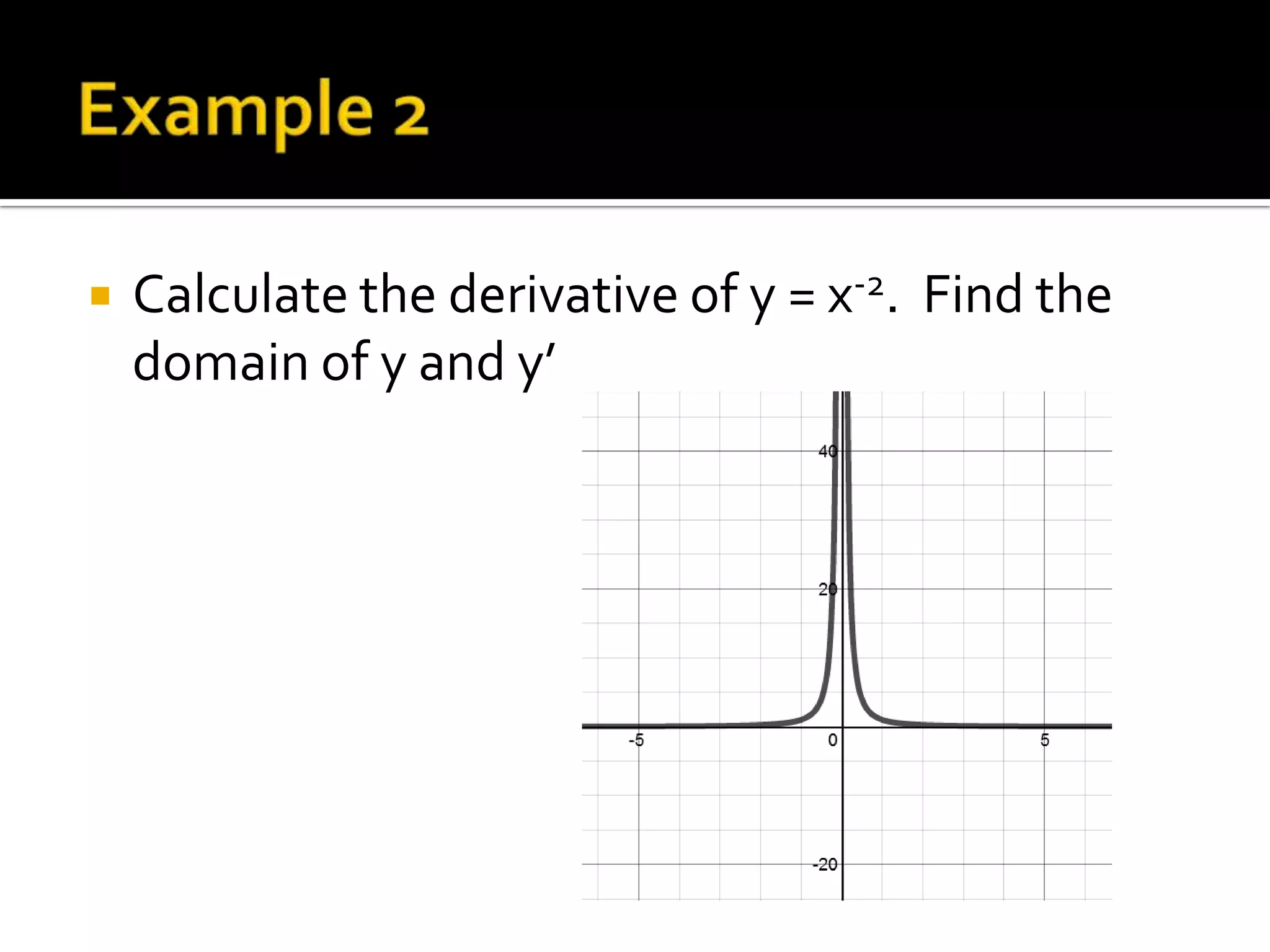
This document covers key concepts in calculus including: - Computing derivatives using notation such as f'(a) and dy/dx - Relationships between differentiability and continuity - Using derivatives to find horizontal tangents, max/min points, and inflection points - Applying derivative rules such as the sum and constant multiple rules - Examples of computing derivatives of various functions and determining differentiability

1. AP Calculus

2.  Derivative f’ (a) for specific values of a

3.  Function f’ (x)

4.  Domain of f’ (x) is all values of x in domain of
f (x) for which the limit exists.
 F’ (x) is differentiable on (a, b) if f ‘(x) exists
for all x in (a, b).
 If f’ (x) exists for all x, then f (x) is
differentiable.

5.  Prove that f (x) = x3 – 12x is differentiable.
Compute f ‘(x) and write the equation of the
tangent line at x = -3.

6.  F ‘(x) = 3x2 – 12
 Equation of tangent line at x = -3
y = 15x + 54

7.  Calculate the derivative of y = x-2. Find the
domain of y and y’

8.  Solution: y’ = -2x-3
 Domain of y: {x| x ≠ 0}
 Domain of y’ : {x| x ≠ 0}
 The function is differentiable.

9.  Another notation for writing the derivative:
 Read “dy dx”
 For the last example y = x-2, the solution could
have been written this way:

10.  For all exponents n,

12.  Calculate the derivative of the function below

13.  Solution:

14. Assume that f and g are differentiable
functions.
 Sum Rule: the function f + g is differentiable
(f + g)’ = f’ + g’
 Constant Multiple Rule: For any constant c,
cf is differentiable and
(cf)’ = cf’

15.  Find the points on the graph of
f(t) = t3 – 12t + 4 where the tangent line(s) is
horizontal.

16.  Solution:

17.  How is the graph of f(x) = x3 – 12x related to
the graph of f’(x) = 3x2 – 12 ?

18. f(x) = x3 – 12 x Decreasing on (-2, 2)
Increasing on (2, ∞)
Increasing on (-∞, -2)
What happens
to f(x) at x = -2
f’(x) = 3x2 - 12 and x = 2??
Graph of f’(x) positive f’(x) is negative f’(x) is positive on (2, ∞)
on (-∞, -2) on (-2,2)
Zeros at -2, 2

19.  Differentiability Implies Continuity
 If f is differentiable at x = c, then f is continuous at
x = c.

20.  Show that f(x) = |x| is continuous but not
differentiable at x = 0.

21.  The function is continuous at x = 0 because

22.  The one-sided limits are not equal:
 The function is not differentiable at x = 0

23.  Local Linearity
 f(x) = x3 – 12x

24.  g(x) = |x|

25.  Show that f(x) = x 1/3 is not differentiable at
x = 0.

26. The limit at x = 0 is infinite
f’(0) =
The slope of the tangent line is
infinite – vertical tangent line