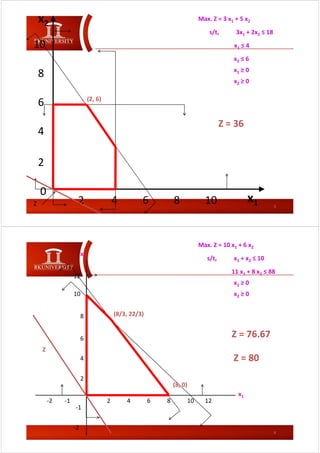
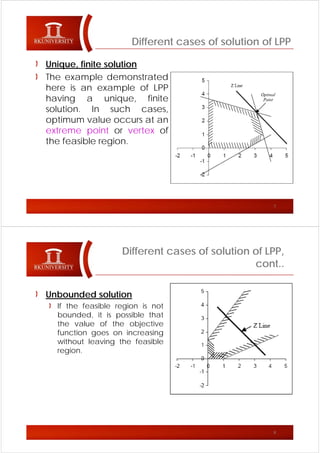
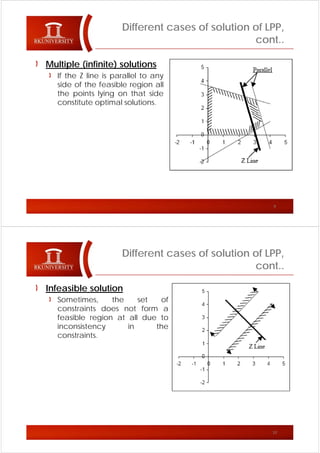
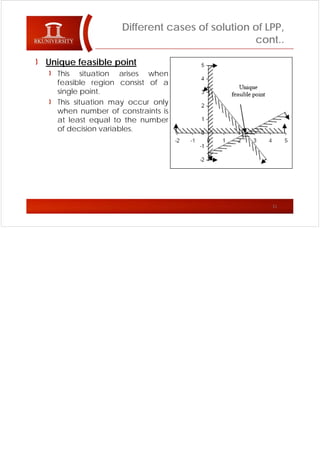
The document discusses the graphical method for solving linear programming problems (LPP), noting that the feasible region must be convex and the optimal solution occurs at an extreme point; it also outlines different cases for the solution such as it being unique and finite, unbounded, having multiple solutions, being infeasible, or having a unique feasible point. The cases discussed include problems having a unique, finite optimal solution; an unbounded feasible region where the objective continues increasing; multiple optimal solutions along a parallel constraint; an infeasible feasible region due to inconsistent constraints; and a single feasible point occurring when constraints equal variables.

1. Graphical method to solve LPPGraphical method to solve LPP
Prof. Keyur P Hirparay p
Assistant Professor
keyur.hirpara@rku.ac.in
9879519312
1
C t d N tConvex set and Non-convex set
Convex set
if any two points of the polygon are selected arbitrarily then
a straight line segment joining these two points lies
completely within the polygoncompletely within the polygon.
Extreme points of convex set are the basic solution to the
LPP
2
Convex Non Convex

2. x2
Max. Z = 3 x1 + 5 x2
s/t, 3x1 + 2x2 ≤ 18
10 x1 ≤ 4
x2 ≤ 6
8 x1 ≥ 0
x2 ≥ 0
6 (2, 6)
4
Z = 36
22
0
2 4 6 8 10 x1
0
Z 3
Max. Z = 10 x1 + 6 x2
s/t, x1 + x2 ≤ 10
x2
11 x1 + 8 x2 ≤ 88
x1 ≥ 0
12
x2 ≥ 0
8
10
(8/3 22/3)
6
8 (8/3, 22/3)
Z = 76.67
4
6
Z
Z = 80
2
(8, 0)
‐1
2 4 6 8 10‐1‐2 12
x1
‐2
4

3. Max. Z = 6 x1 + 5 x2
s/t, 2x1 ‐ 3x2 ≤ 5
x1 + 3x2 ≤ 11
4 x1 + x2 ≤ 15
x2
x1 ≥ 0
x2 ≥ 0
4
5
3
4
(3.09, 2.64)
2
3
Z = 31.73
1
Z
‐1
1 2 3 4 5‐1‐2 x1
‐2
5
x2
Min. Z = 3 x1 + 5 x2
s/t, 3x1 + 2x2 ≥ 18
10 x1 ≤ 4
x2 ≤ 6
Z
8 x1 ≥ 0
x2 ≥ 0
6
4
Z = 27
2
(4, 3)
2
0
2 4 6 8 10 x1
0
6

4. Diff t f l ti f LPPDifferent cases of solution of LPP
Unique finite solutionUnique, finite solution
The example demonstrated
here is an example of LPPhere is an example of LPP
having a unique, finite
solution. In such cases,
optimum value occurs at an
extreme point or vertex of
th f ibl ithe feasible region.
7
Different cases of solution of LPP,
contcont..
Unbounded solution
If the feasible region is not
bounded it is possible thatbounded, it is possible that
the value of the objective
function goes on increasing
ith t l i th f iblwithout leaving the feasible
region.
8

5. Different cases of solution of LPP,
contcont..
Multiple (infinite) solutionsMultiple (infinite) solutions
If the Z line is parallel to any
side of the feasible region allg
the points lying on that side
constitute optimal solutions.
9
Different cases of solution of LPP,
contcont..
Infeasible solutionInfeasible solution
Sometimes, the set of
constraints does not form a
f i ifeasible region at all due to
inconsistency in the
constraints.
10

6. Different cases of solution of LPP,
contcont..
Unique feasible pointUnique feasible point
This situation arises when
feasible region consist of a
i isingle point.
This situation may occur only
when number of constraints iswhen number of constraints is
at least equal to the number
of decision variables.
11