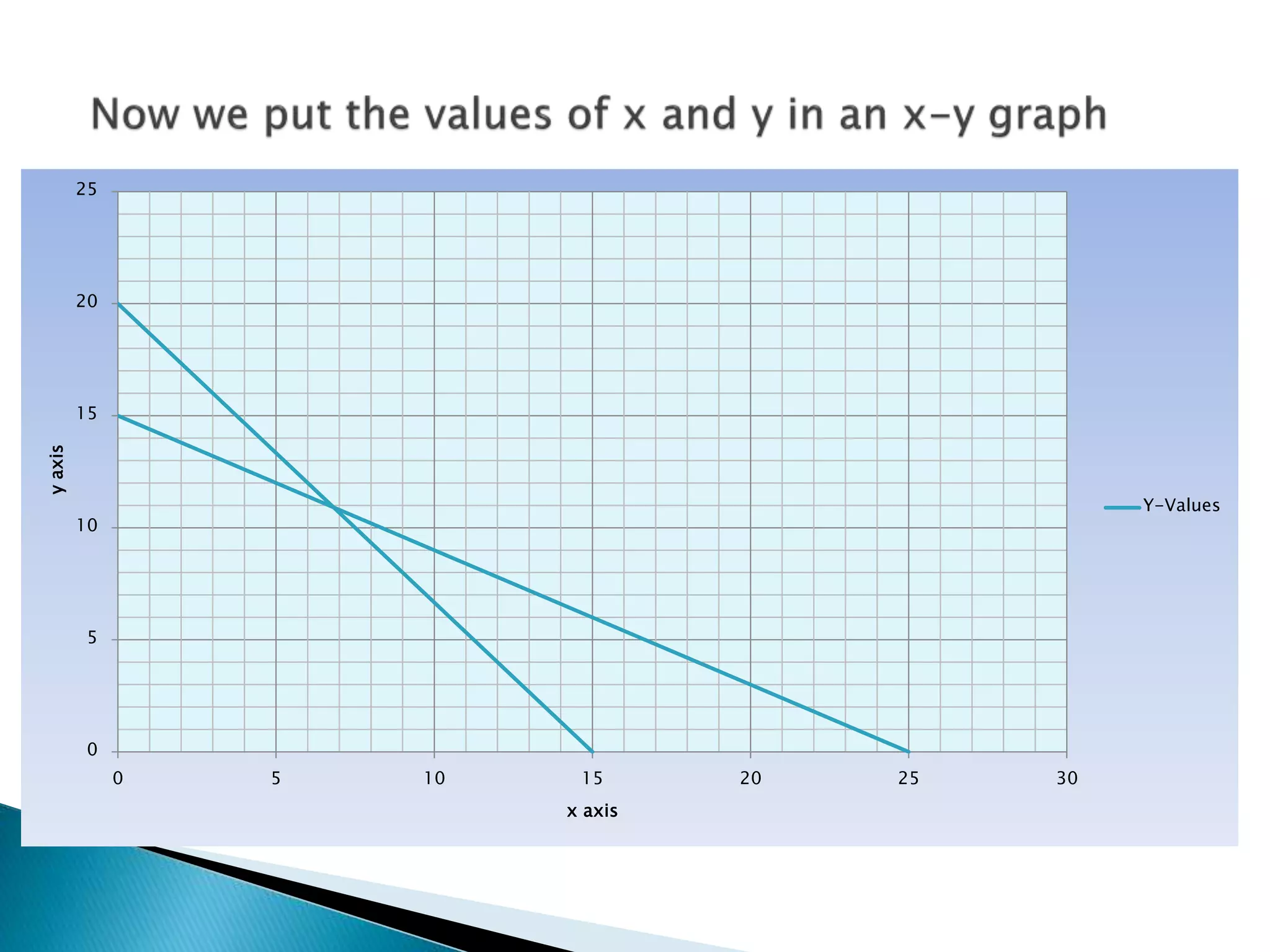
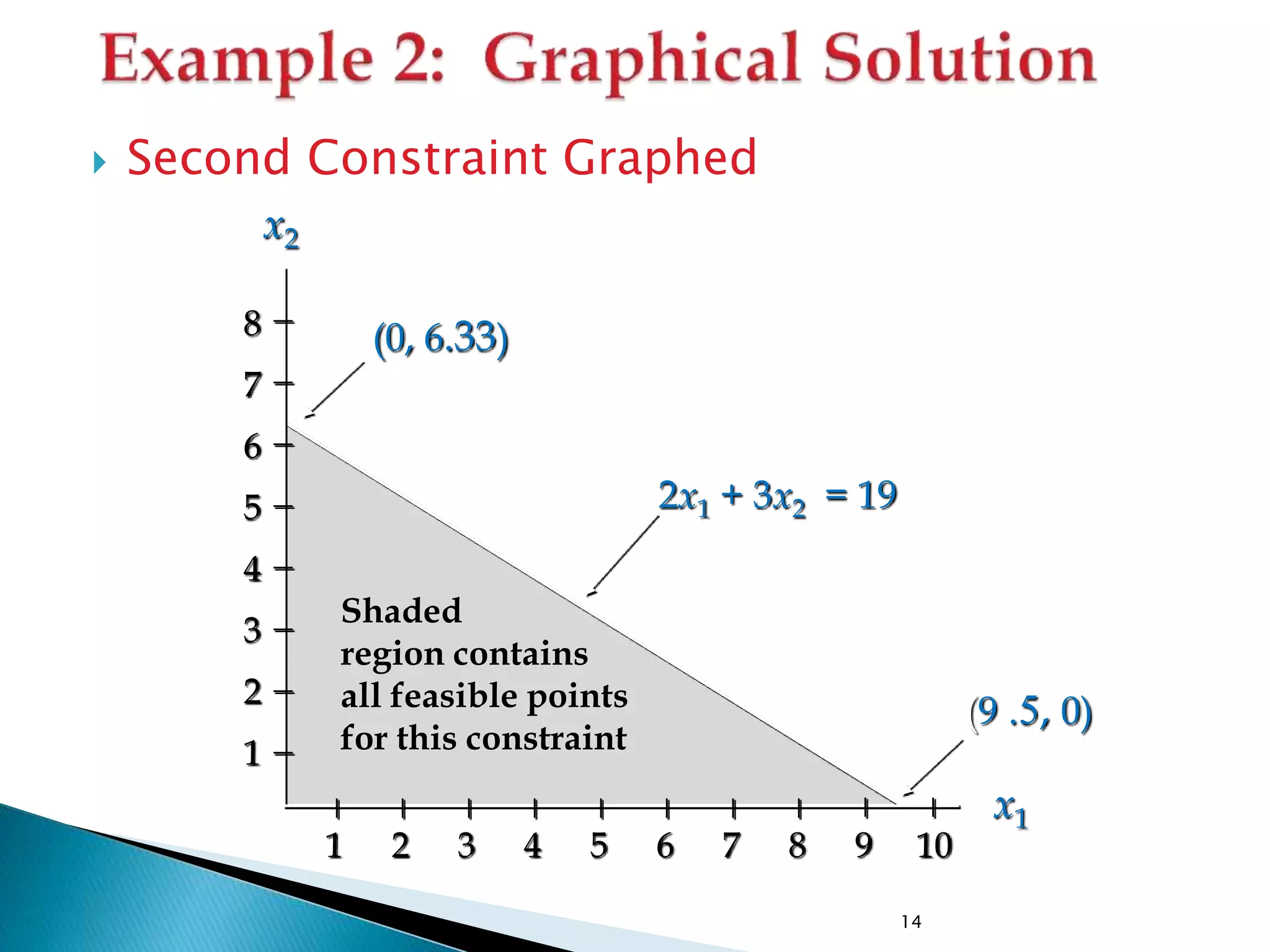
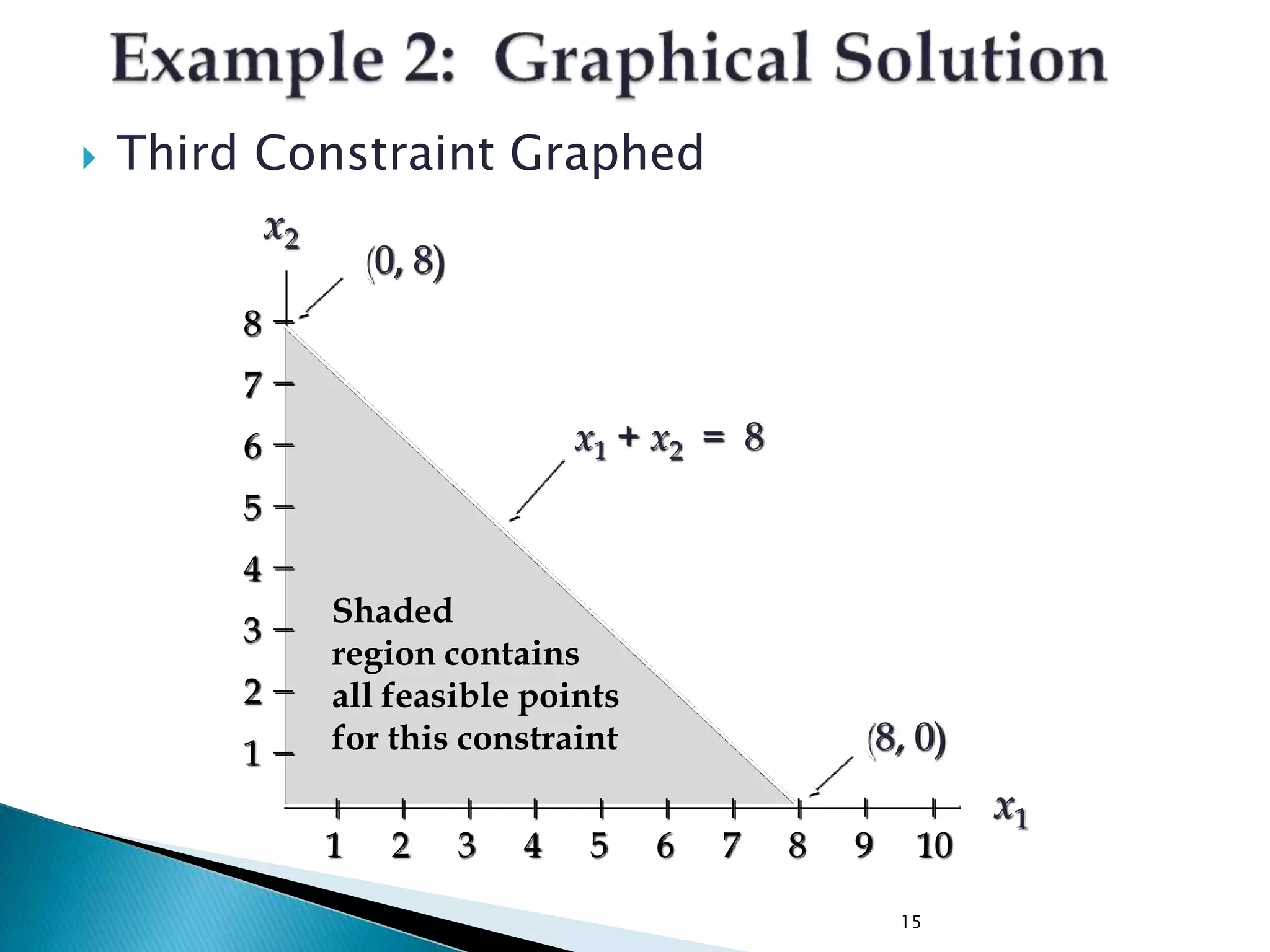
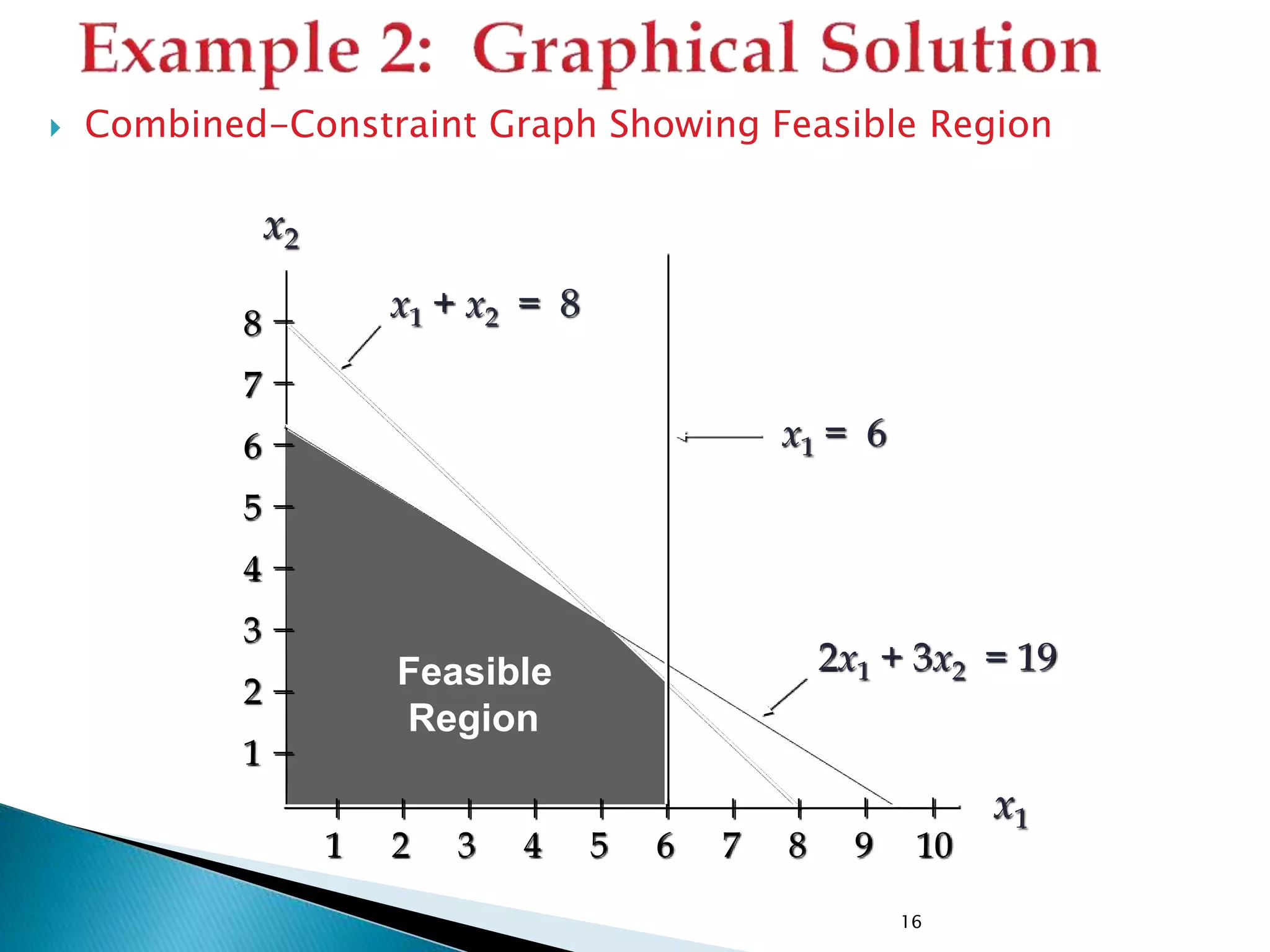
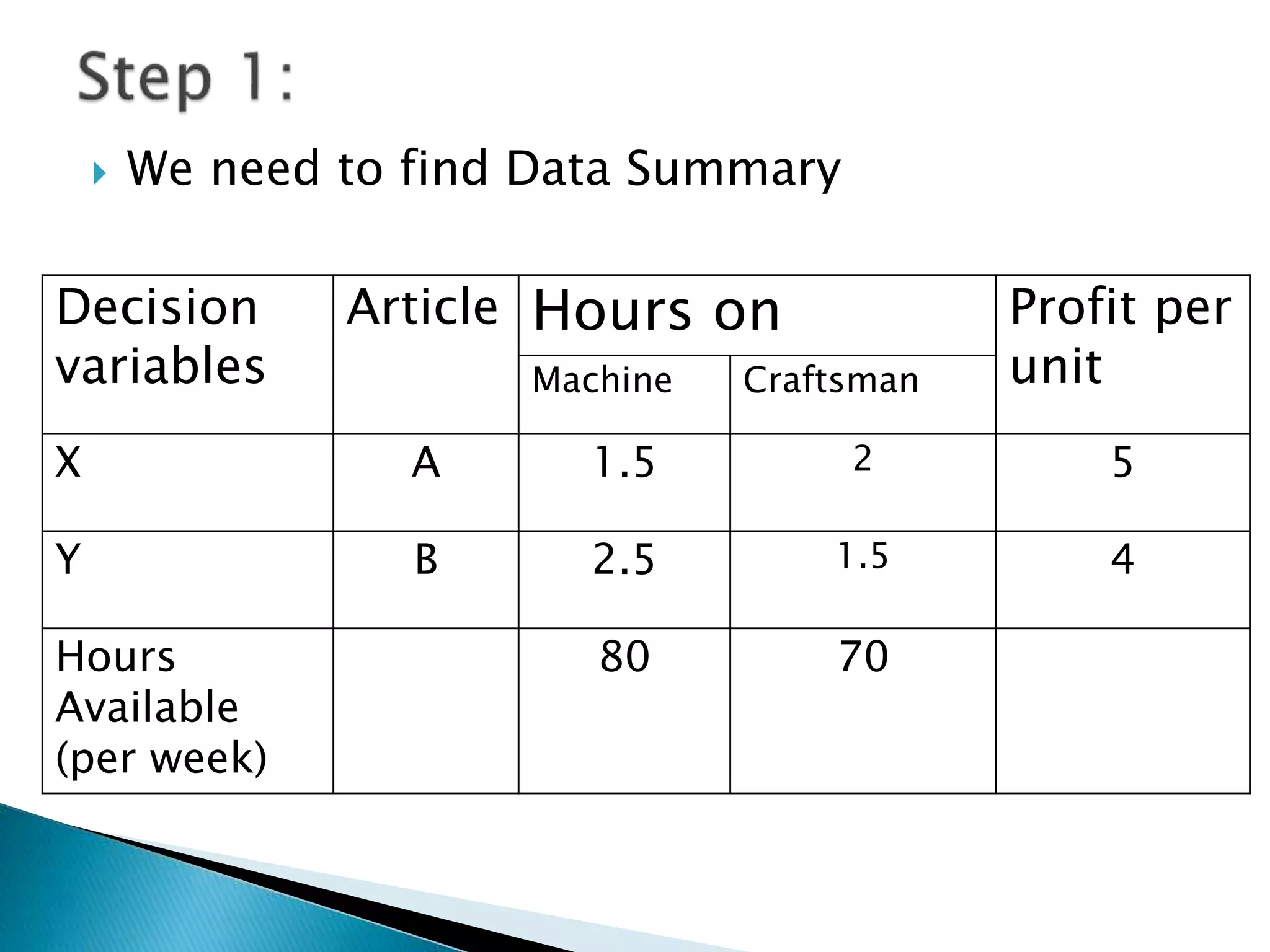
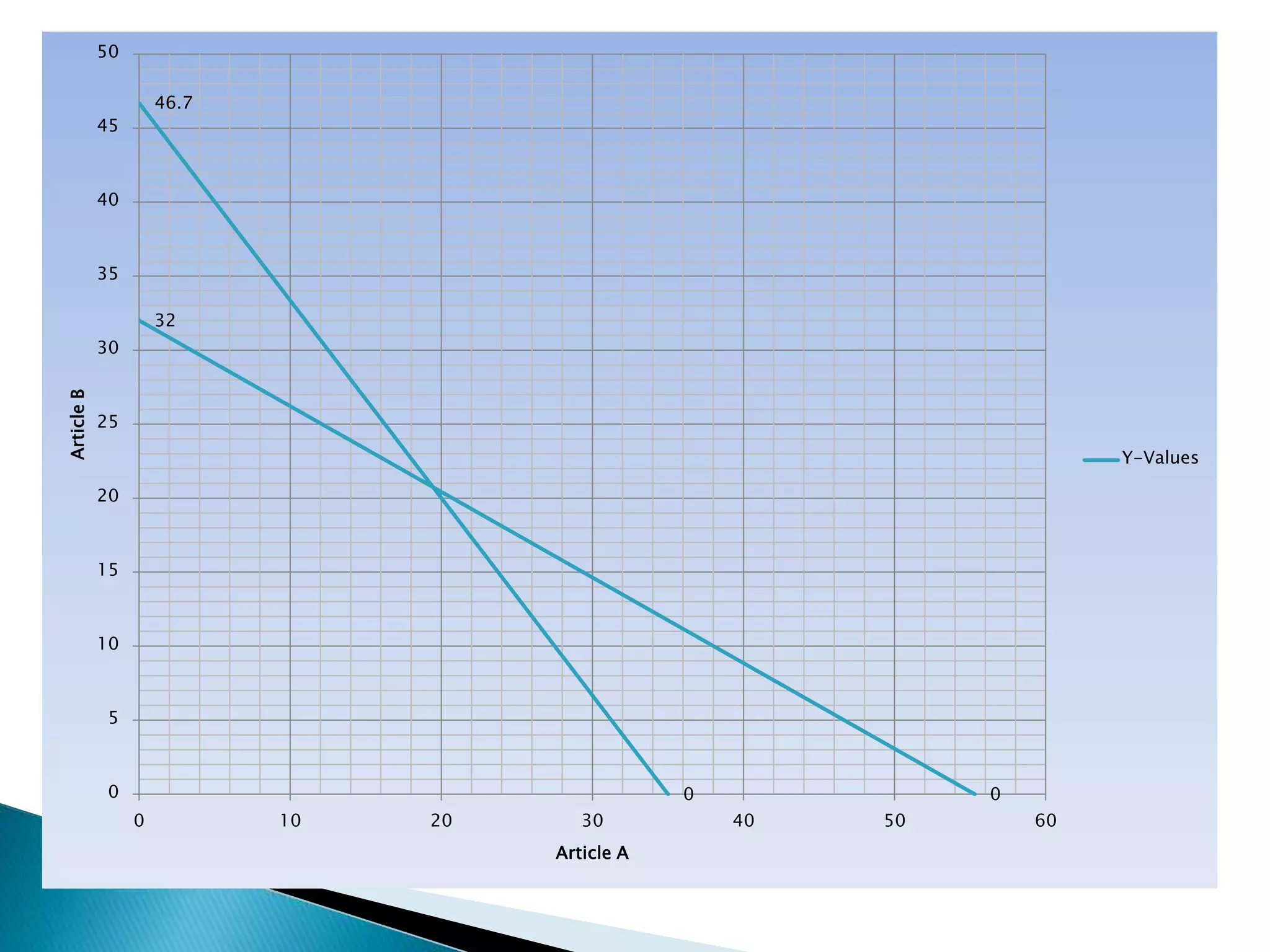
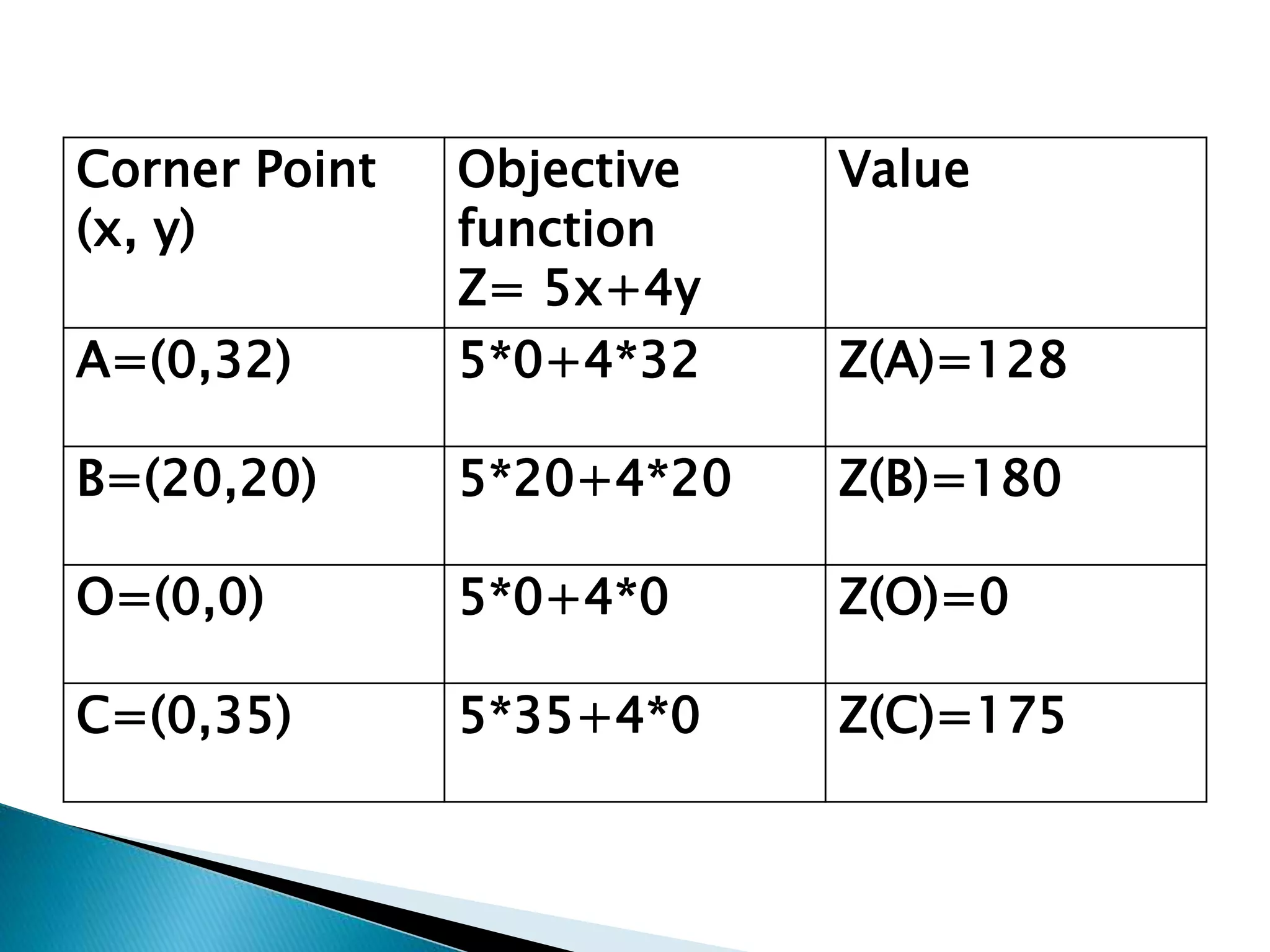
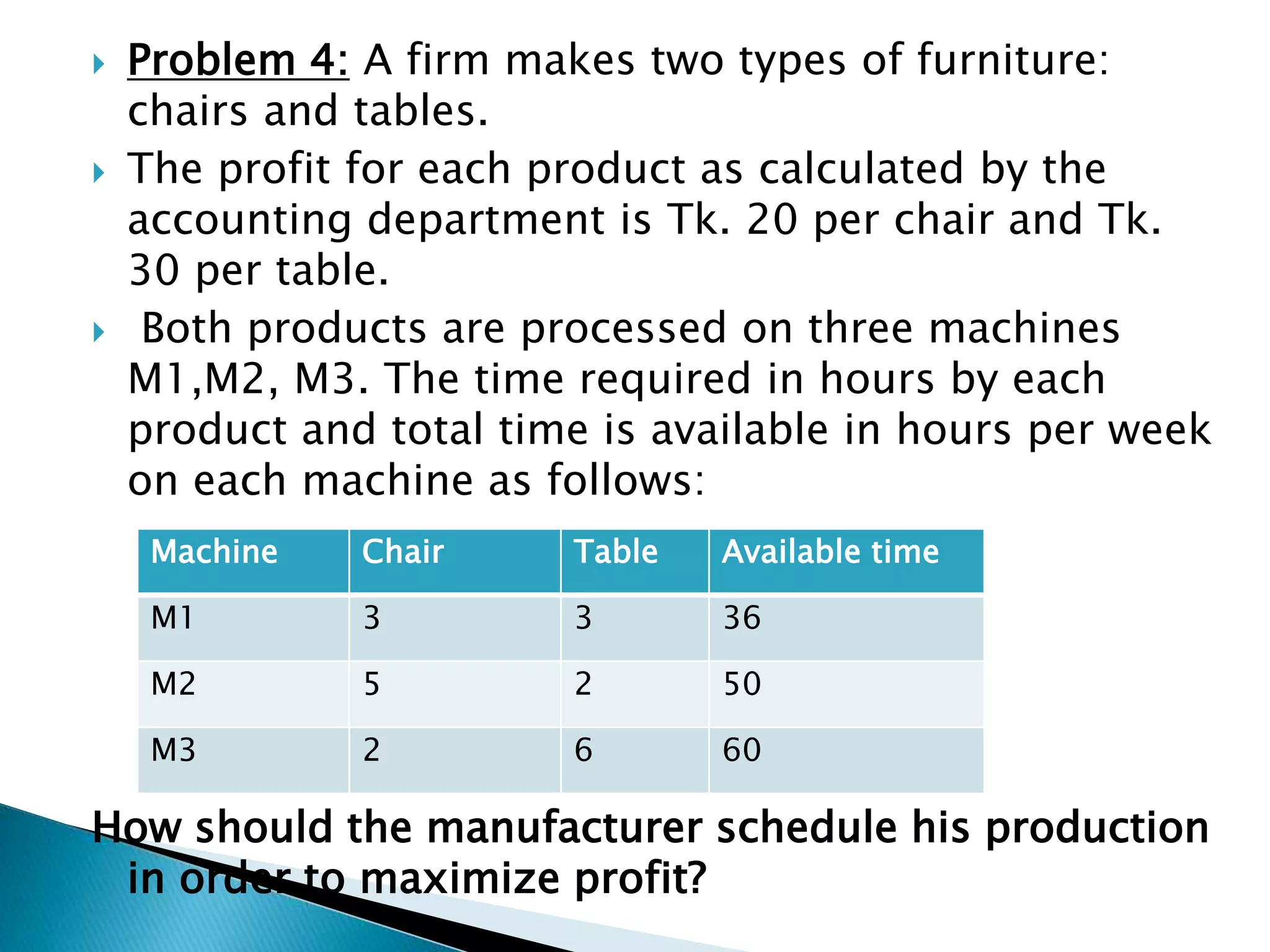
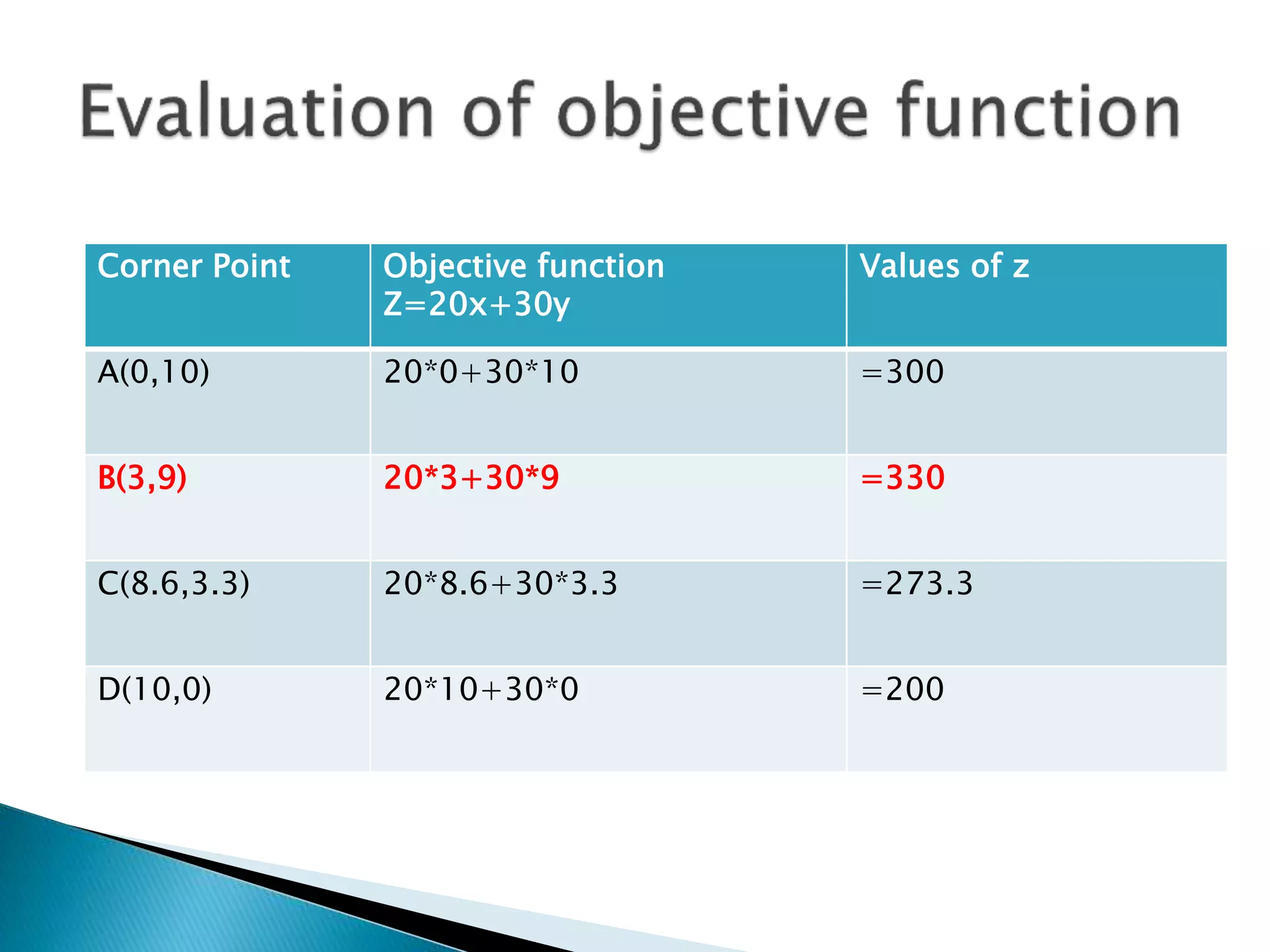
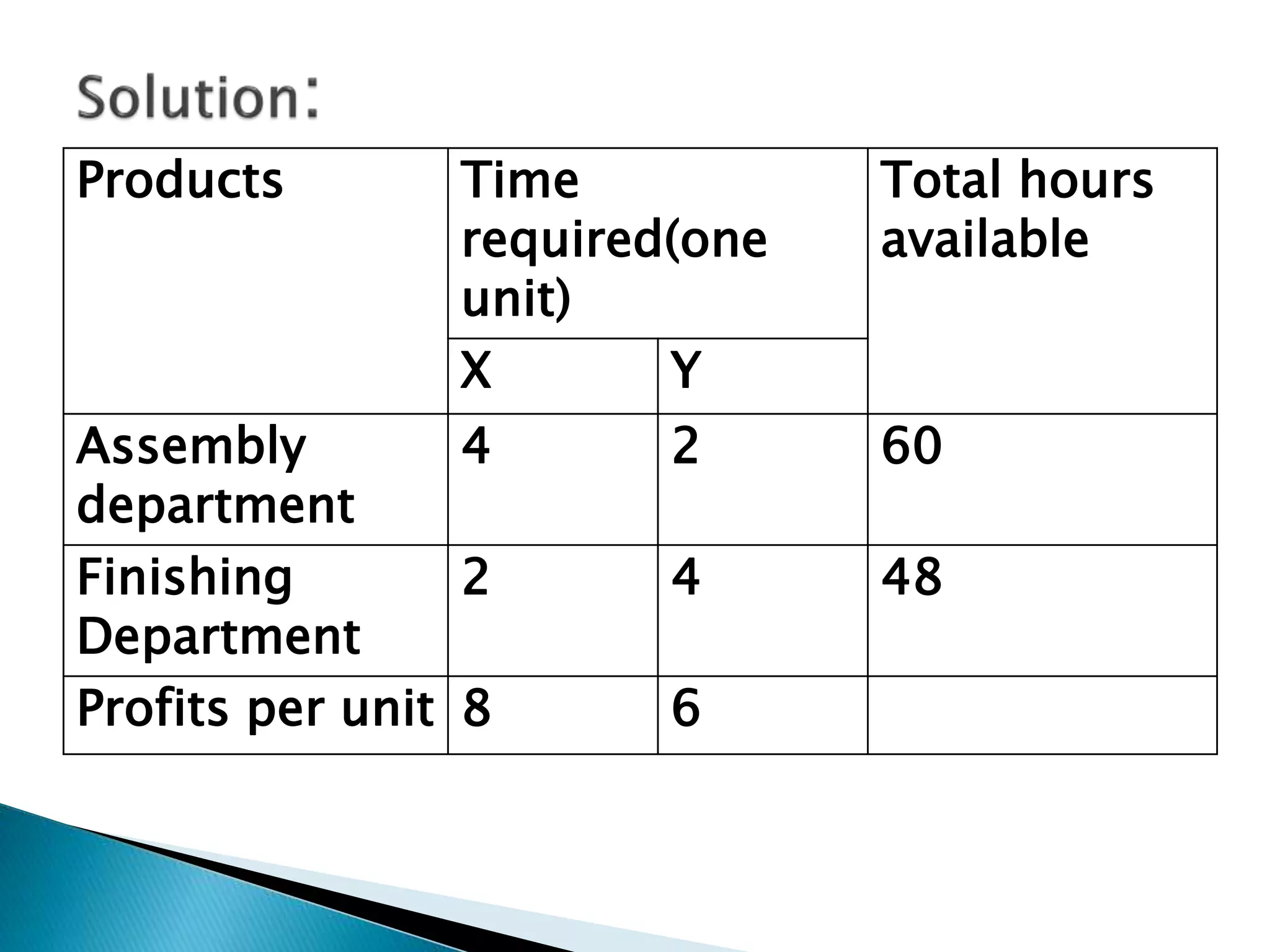
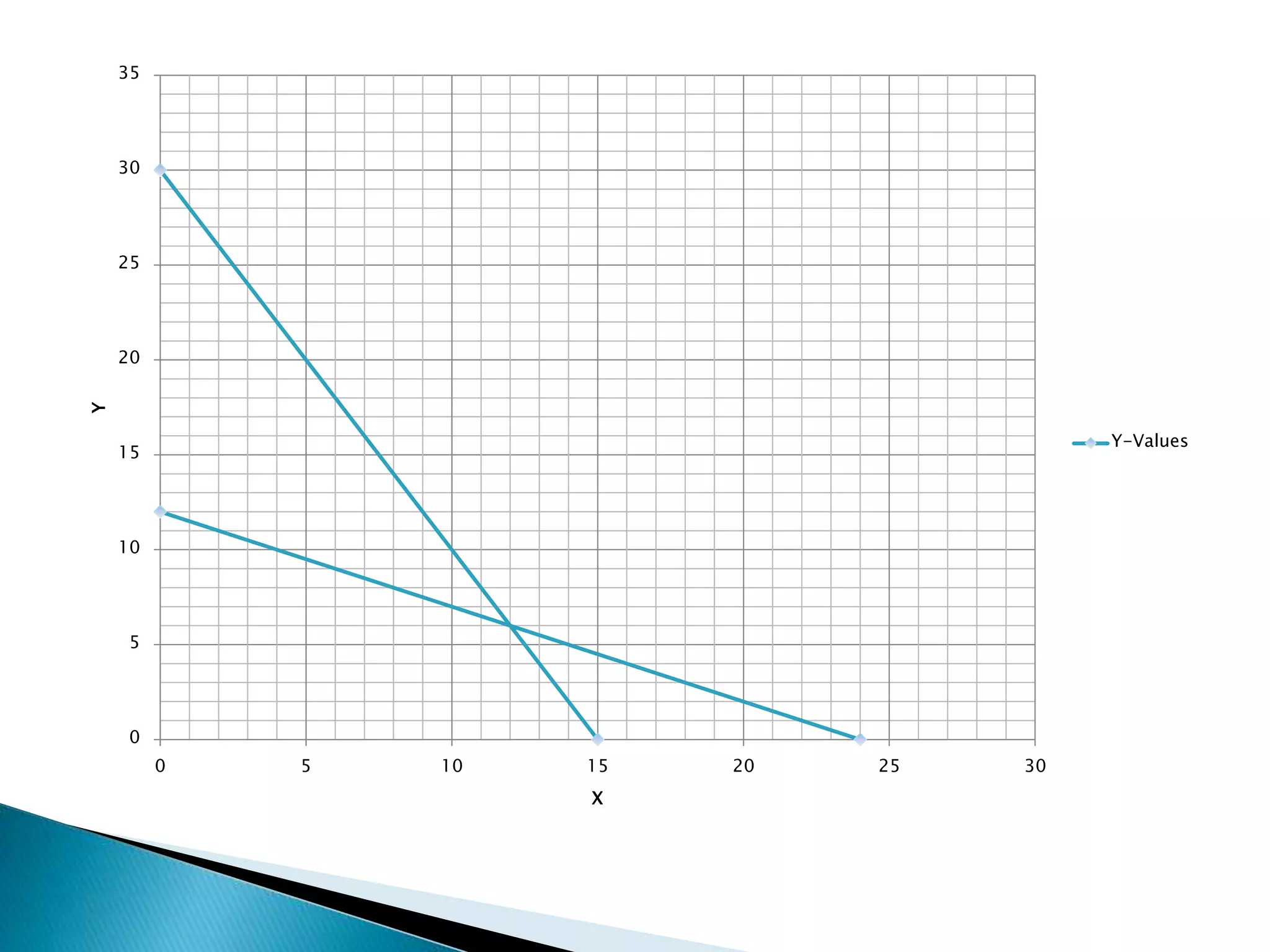
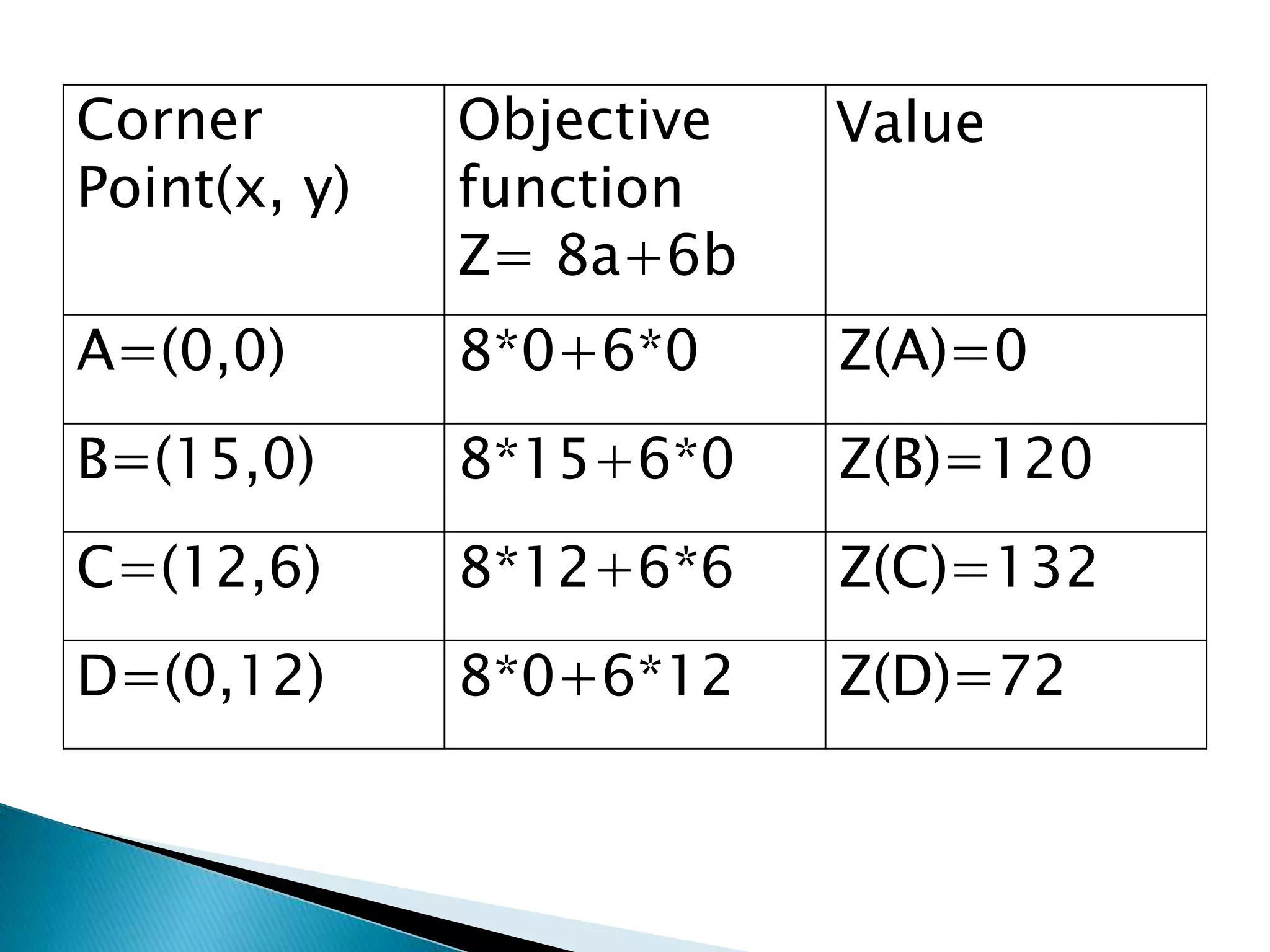
The document describes how to formulate and solve linear programming problems by defining the components of a linear programming problem, describing how to model real-world problems as linear programs, and outlining two methods, graphical and simplex, to solve linear programming problems. It then provides examples of solving linear programming problems using these steps and methods.

2.  Describe the type of Linear Programming
Problem (LPP)
 Formulate a linear programming model from
a description of a problem
 Solve linear programming problems using the
 1. Graphical method
 2. Simplex method

3.  Definition: LPP is a minimization (or
maximization) problem where we are asked
to minimize (or maximize) a given linear
function
 subject to one or more linear inequality
constraints.
 For example, minimized z=ax+by
 Where ax+by<0
 x>0 or y>0

4.  Objective Function:
Z=c1x1+c2x2+………+ cnxn
 Which is to be minimized or
maximized is called the objective
function of the General L.P.P.
 Constraints: The inequalities are
called the constraints of General L.P.P.
 Non- negative restrictions: The set of
inequalities is usually known as the
set of non- negative restrictions of
General L.P.P.

5.  Solution: Values of unknowns x1, x2, ......, xn
which satisfy the constraints of a General
L.P.P. is called a solution to the General
L.P.P.
 Feasible Solution: Any solution to a General
L.P.P. which satisfies the non-negative
restrictions of the problem, called feasible
solution to the General L.P.P.
 Optimum Solution: Any feasible solution
which optimizes (Minimize or Maximizes)
the objective function of a General L.P.P. is
called an optimum solution to the General
L.P.P.

7.  Solve a linear programming problem
 Find the minimum value of
 Z=3x+8y objective function
 4x+3y≥60
 3x+5y≤75 constraints
 x, y≥ o

8.  From 4x+3y≥60 we can find the value
of X and Y as:
If X 0 15
Then Y 20 0

9.  From 3x+5y≤75 we can find the value
of X and Y as:
If X 0 25
then Y 15 0

10. 0
5
10
15
20
25
0 5 10 15 20 25 30
yaxis
x axis
Y-Values

11. Corner Point Objective function
Value
Z=3x+8y
Remarks
A(15,0) 3*15+8*0=45
B(25,0) 3*25+8*0=75
C(6.8, 10.9)
So the optimum value of
x=6.8 and y=10.9
3*6.8+8*10.9=107.66 Maximum

12. 12
Maximum z= 5x1 + 7x2
s.t. x1 < 6
2x1 + 3x2 < 19
x1 + x2 < 8
x1 > 0 and x2 > 0
Objective
Function
“Regular”
Constraints
Non-negativity
Constraints

13. 13
 First Constraint Graphed
x2
x1
x1 = 6
(6, 0)
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9 10
Shaded region
contains all
feasible points
for this constraint

14. 14
 Second Constraint Graphed
2x1 + 3x2 = 19
x2
x1
(0, 6.33)
(9 .5, 0)
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9 10
Shaded
region contains
all feasible points
for this constraint

15. 15
 Third Constraint Graphed
x2
x1
x1 + x2 = 8
(0, 8)
(8, 0)
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9 10
Shaded
region contains
all feasible points
for this constraint

16. 16
x1
x2
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9 10
2x1 + 3x2 = 19
x1 + x2 = 8
x1 = 6
 Combined-Constraint Graph Showing Feasible Region
Feasible
Region

17. Corner point Objective function
Z= 5x1 + 7x2 Remark
A(0,0) 5*0+7*0=0
B(0, 6.33) 5*0+7*6.33=44.31
C(5,3) 5*5+7*3=46 Maximum
D(6,2) 5*6+7*2=44
E(6,0) 5*6+7*0=30

18.  Problem 3: A factory manufactures two articles A
and B.
 To manufacture the article A, a certain machine has
to be worked for 1.5 hours and in addition a
craftsman has to work for 2 hours.
 To manufacture the article B, the machine has to be
worked for 2.5 hours and in addition a craftsman
has to work for 1.5 hours.
 In a week the factory can avail of 80 hours of
machine time and 70 hours of craftsman time.
 The profit on each article A is Tk.5 an that on
each article B is Tk.4.
 If all the articles produced can be sold away,
 Find how many of each kind should be produced to
earn the maximum profit per week?

19.  We need to find Data Summary
Decision
variables
Article Hours on Profit per
unitMachine Craftsman
X A 1.5 2 5
Y B 2.5 1.5 4
Hours
Available
(per week)
80 70

20.  Where,
 x = Number of units of article A
 y = Number of units of article B
 Thus, the given problem is formulated as a
L.P.P as follows:
 Maximize Z= 5x+4y (Objective Function)
 Subject to the constraint:
 1.5x+2.5y ≤80
 2x+1.5y ≤70
 x ≥0 , y≥0

21.  Then for 1.5x+2.5y ≤80,
If, x 0 55.3
Then,y 32 0

22.  & for 2x+1.5y ≤70
IF,X 0 35
Then,y 46.7 0

23. 32
0
46.7
00
5
10
15
20
25
30
35
40
45
50
0 10 20 30 40 50 60
ArticleB
Article A
Y-Values

24. Corner Point
(x, y)
Objective
function
Z= 5x+4y
Value
A=(0,32) 5*0+4*32 Z(A)=128
B=(20,20) 5*20+4*20 Z(B)=180
O=(0,0) 5*0+4*0 Z(O)=0
C=(0,35) 5*35+4*0 Z(C)=175

25.  For point B (20, 20) the
objective value is maximum.
So the solution is for
 article A: 20 units and
 and article B: 20 units
 to earn the maximum profit
per week

26.  Problem 4: A firm makes two types of furniture:
chairs and tables.
 The profit for each product as calculated by the
accounting department is Tk. 20 per chair and Tk.
30 per table.
 Both products are processed on three machines
M1,M2, M3. The time required in hours by each
product and total time is available in hours per week
on each machine as follows:
How should the manufacturer schedule his production
in order to maximize profit?
Machine Chair Table Available time
M1 3 3 36
M2 5 2 50
M3 2 6 60

27.  Let x= numbers of chairs
 y= numbers of tables
 In this case, the objective
function is Maximize Z=20x+30y
 And the constraint equations are
 3x+3y≤36
 5x+2y≤50
 2x+6y≤60

28.  For 3x+3y≤36 the graph point will be
 For 5x+2y≤50 the graph will be
X 0 12
Y 12 0
X 0 10
Y 25 0

29.  For 2x+6y≤60 the graph will be
X 0 30
Y 10 0

30. Corner Point Objective function
Z=20x+30y
Values of z
A(0,10) 20*0+30*10 =300
B(3,9) 20*3+30*9 =330
C(8.6,3.3) 20*8.6+30*3.3 =273.3
D(10,0) 20*10+30*0 =200

31.  So the maximum value of z is
330, and this occurs when x=3
and y=9.
 so the manufacturer should use
330 units to maximize the
production.

32.  Problem 5. A company produces two articles X and
Y.There are two departments through which the
articles are processed. That is assembling and
finishing.
 The potential capacity of the assembling
department is 60hours a week and that of the
finishing department is 48 hours a week.
 Production of one unit of X requires 4 hours in
assembling and 2 hours in finishing.
 Each of the unit Y requires 2 hours in assembly and
4 hours in finishing.
 If profit is tk.8 for each unit of X and Tk.6 for each
unit of Y,
 Find out the number of units of X and Y to be
prepared each week to give maximum profit??

33. Products Time
required(one
unit)
Total hours
available
X Y
Assembly
department
4 2 60
Finishing
Department
2 4 48
Profits per unit 8 6

34.  Objective Function: Z= 8a+6b
 Subject to constraints:
 4a+2b ≤ 60
 2a+4b ≤ 48
 Non-negativity requirement: X≥0,Y≥0

35.  Then for 4a+2b ≤60,,
X 0 15
y 30 0

36. & for 2a+4b ≤48
X 0 24
Y 12 0

37. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30
Y
X
Y-Values

38. Corner
Point(x, y)
Objective
function
Z= 8a+6b
Value
A=(0,0) 8*0+6*0 Z(A)=0
B=(15,0) 8*15+6*0 Z(B)=120
C=(12,6) 8*12+6*6 Z(C)=132
D=(0,12) 8*0+6*12 Z(D)=72

39.  For point C (12, 6) the objective
function z is maximum. So the
solution is to get the maximum
produced article, article x must
produce 12 units and article y
must produce 6 unit

40.  1. A calculator company produces a scientific
calculator and a graphing calculator. Long-term
projections indicate an expected demand of at
least 100 scientific and 80 graphing calculators
each day.
 Because of limitations on production capacity, no
more than 200 scientific and 170 graphing
calculators can be made daily.
 To satisfy a shipping contract, a total of at least
200 calculators much be shipped each day.
 If each scientific calculator sold results in a $2
loss, but each graphing calculator produces a $5
profit, how many of each type should be made
daily to maximize net profits?

41.  You need to buy some file cabinets. You know that
Cabinet X costs $10 per unit, requires 6 square feet
of floor space, and holds 8 cubic feet of files.
 Cabinet Y costs $20 per unit, requires 8 square feet
of floor space, and holds 12 cubic feet of files.
 You have been given $140 for this purchase, though
you don't have to spend that much.
 The office has room for no more than 72 square feet
of cabinets.
 How many of which model should you buy, in order to
maximize storage volume?
 What is the maximum storage?