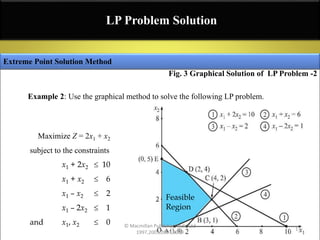
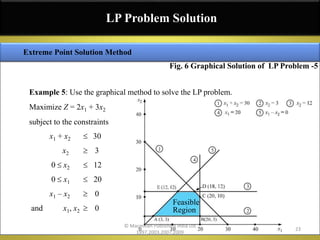
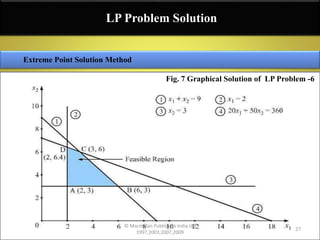
The document discusses linear programming (LP) and the graphical method for solving LP problems, highlighting key concepts such as feasible and infeasible solutions, basic feasible solutions, and the definition of optimal solutions. Methods for finding optimal solutions through graphical representation and evaluation of extreme points in the feasible region are outlined, including step-by-step approaches to constructing LP models and solving examples. Multiple examples are provided to illustrate the application of these techniques in maximizing or minimizing objective functions under given constraints.

![“People realize that[technology]certainly is a tool.
This tool can be used to enhance operations, Improve
efficiencies and really add value to academic
research and teaching exercises.”
Peter Murray
2
© Macmillan Publishers India Ltd
1997,2003,2007,2009](https://image.slidesharecdn.com/lecture5-712946linearprogrammingthegraphicalmethod-240422033715-2c4cf39f/85/Lecture5-7_12946_Linear-Programming-The-Graphical-Method-pptx-2-320.jpg)