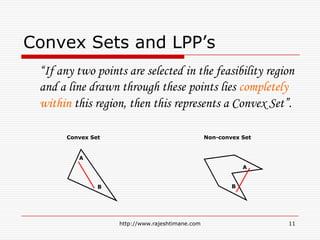
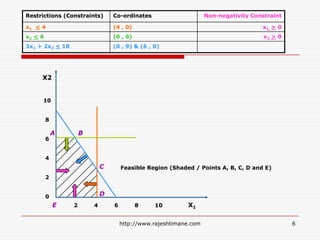
The document explains the fundamentals of linear programming, including definitions of key terms such as decision variables, objective functions, and constraints. It illustrates how to formulate an optimization problem with linear functions and visualizes feasible solutions and optimal outcomes within a constraint graph. The optimal solution is determined by evaluating the corner points of the feasible region to find the best result for the objective function.

1. Linear Programming
Terminology

2. What is a Mathematical Model ?
F=ma
‘Mathematical Expressions’
o Here m and a are called as ‘Decision Variables’
o F can be called as ‘Objective Functions’
o Now, F can be controlled or restricted by limiting m or
a … say m < 50 kg …here, m can be called as a
‘Constraint’
o Similarly if a > o …always, then this condition is called
as ‘Non-Negativity Condition’
http://www.rajeshtimane.com 2

3. Illustration:
Maximize: Z = 3x1 + 5x2 Objective
Function
Subject to restrictions:
x1 <4
Functional
2x2 < 12 Constraints
3x1 + 2x2 < 18
Non negativity condition
x1 >0 Non-negativity
x2 >0 constraints
http://www.rajeshtimane.com 3

4. What is Linear Programming (LP)?
 The most common application of LP is allocating
limited resources among competing activities in a
best possible way i.e. the optimal way.
 The adjective linear means that all the mathematical
functions in this model are required to be linear
functions.
 The word programming does not refer to computer
programming; rather, essentially a synonym for
planning.
http://www.rajeshtimane.com 4

5. Graphical Solution
Ex) Maximize: Z = 3x1 + 5x2
Subject to restrictions:
x1 < 4
2x2 < 12 i.e. x2 < 6
3x1 + 2x2 < 18
Non negativity condition
x1, x2 > 0
Solution: finding coordinates for the constraints (assuming perfect equality), by putting
one decision variable equal to zero at a time.
Restrictions (Constraints) Co-ordinates
x1 < 4 (4 , 0)
x2 < 6 (0 , 6)
3x1 + 2x2 < 18 (0 , 9) & (6 , 0)
http://www.rajeshtimane.com 5

6. Restrictions (Constraints) Co-ordinates Non-negativity Constraint
x1 < 4 (4 , 0) x1, > 0
x2 < 6 (0 , 6) x2 > 0
3x1 + 2x2 < 18 (0 , 9) & (6 , 0)
X2
10
8
A B
6
4
C Feasible Region (Shaded / Points A, B, C, D and E)
2
0 D
E 2 4 6 8 10 X1
http://www.rajeshtimane.com 6

7. Feasible Solutions
 Try co-ordinates of all the corner points of
the feasible region.
 The point which will lead to most
satisfactory objective function will give
Optimal Solution.
 Note: for co-ordinates at intersection; solve
the equations (constraints) of the two lines
simultaneously.
http://www.rajeshtimane.com 7

8. Optimal Solution
Corner Limiting Constraint Co-ordinate Max. Z= 3x1 + 5x2
A x2 = 6 (0 , 6) 30
B x2 = 6 & 3x1 + 2x2 = 18 (2 , 6) 36
C x1 = 4 & 3x1 + 2x2 = 18 (4 , 3) 27
D x1 = 4 (4 , 0) 12
E Origin (0 , 0) 0
From the above table, Z is maximum at point ‘B’ (2 , 6) i.e. The
Optimal Solution is:
X1 = 2 and
X2 = 6 ANSWER
http://www.rajeshtimane.com 8

9. What is Feasibility ?
 Feasibility Region
[Dictionary meaning of feasibility is possibility]
“The region of acceptable values of the
Decision Variables in relation to the
given Constraints (and the Non-Negativity
Restrictions)”
http://www.rajeshtimane.com 9

10. What is an Optimal Solution ?
 It is the Feasible Solution which Optimizes.
i.e. “provides the most beneficial result for the specified
objective function”.
 Ex: If Objective function is Profit then Optimal Solution
is the co-ordinate giving Maximum Value of „Z‟…
While; if objective function is Cost then the optimum
solution is the coordinate giving Minimum Value of „Z‟.
http://www.rajeshtimane.com 10

11. Convex Sets and LPP’s
“If any two points are selected in the feasibility region
and a line drawn through these points lies completely
within this region, then this represents a Convex Set”.
Convex Set Non-convex Set
A
A
B B
http://www.rajeshtimane.com 11