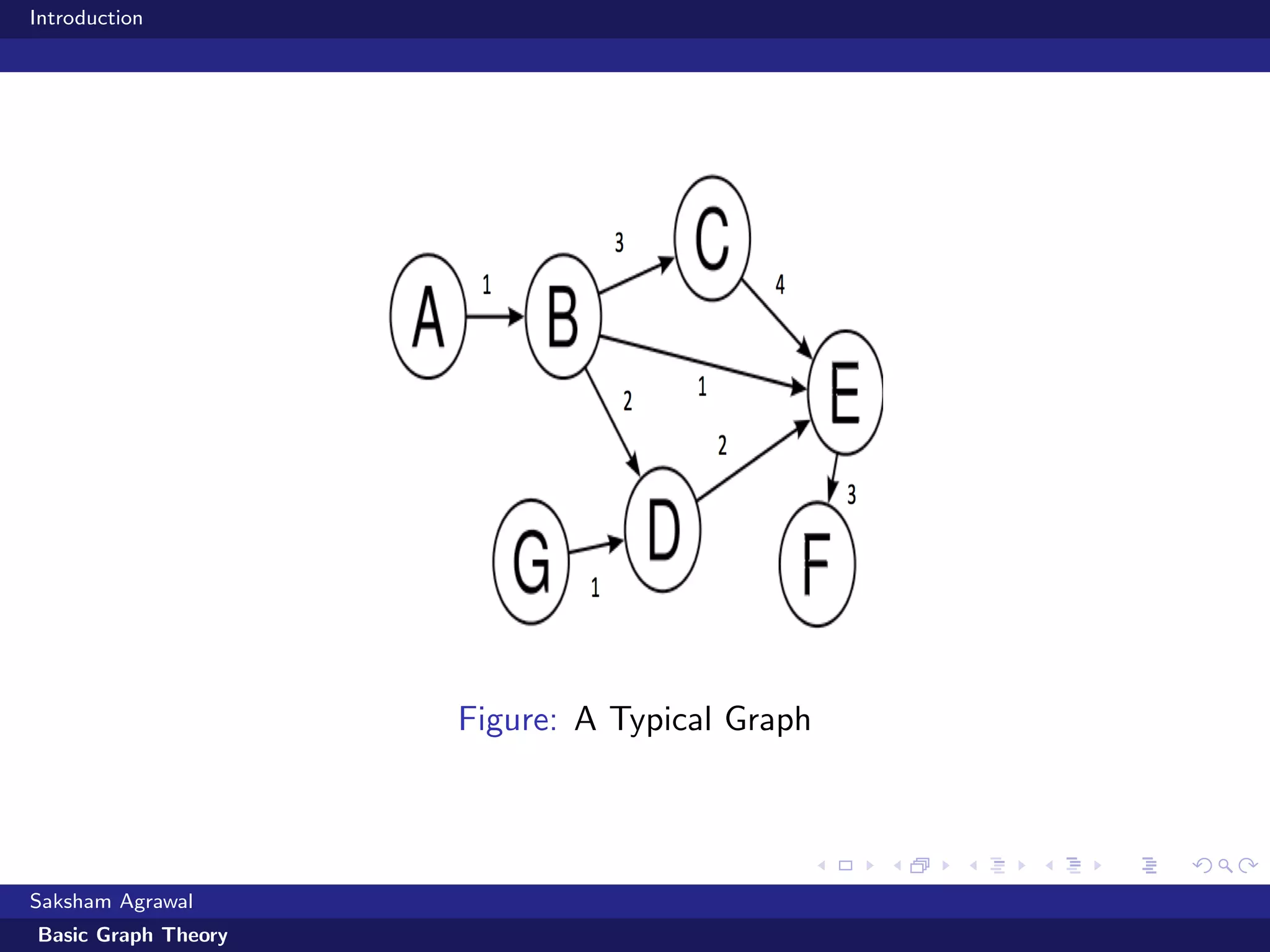
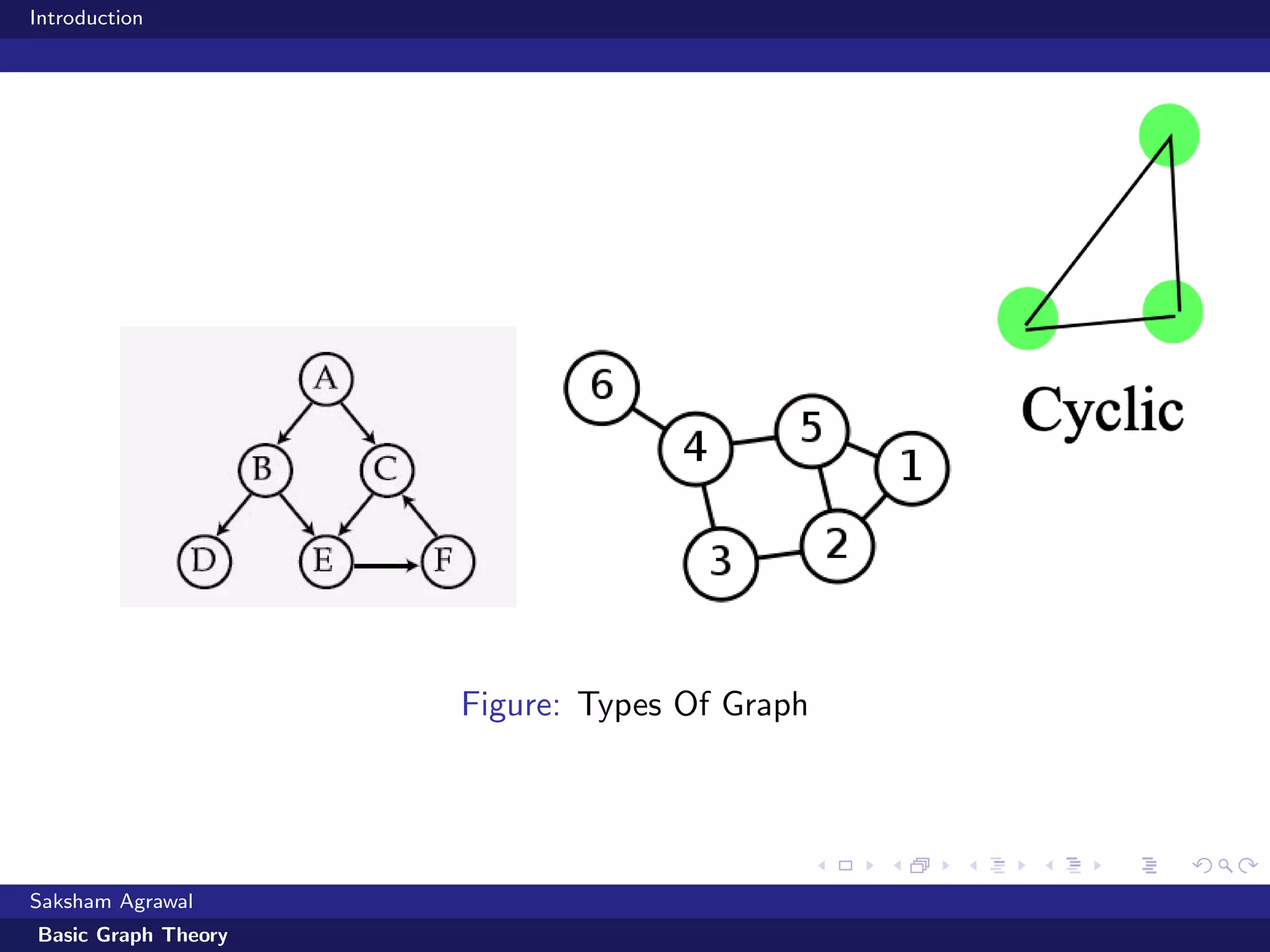
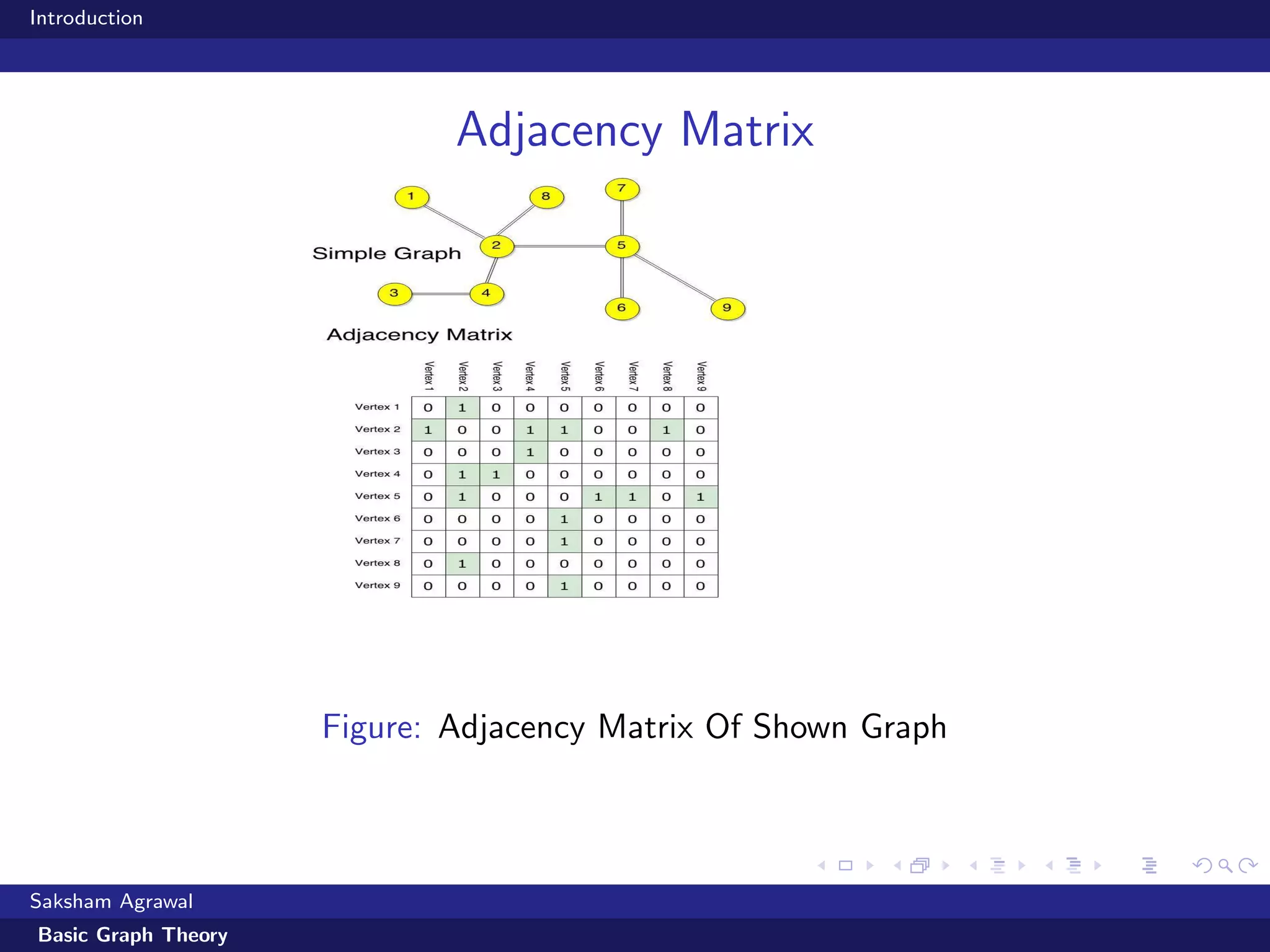
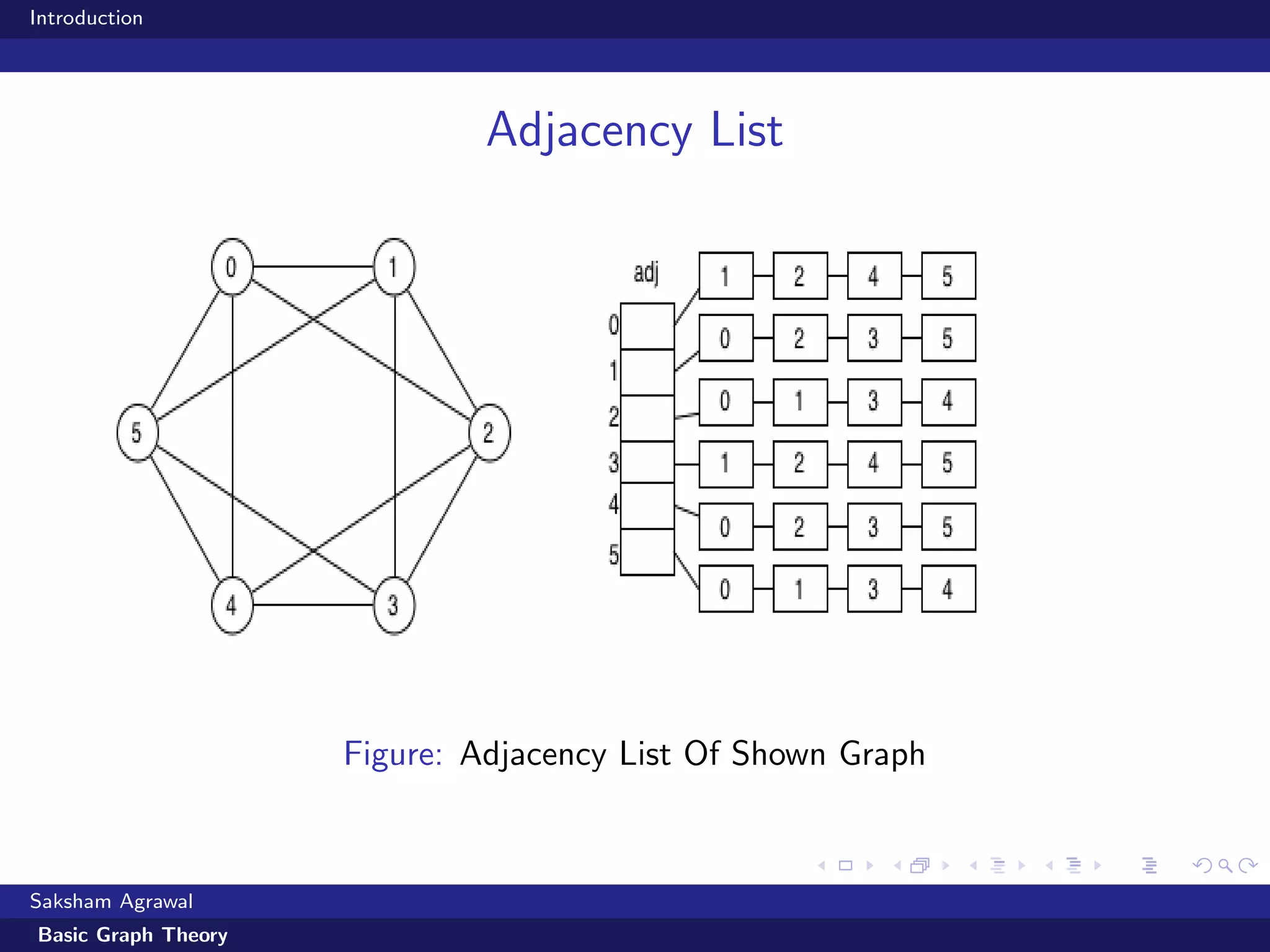
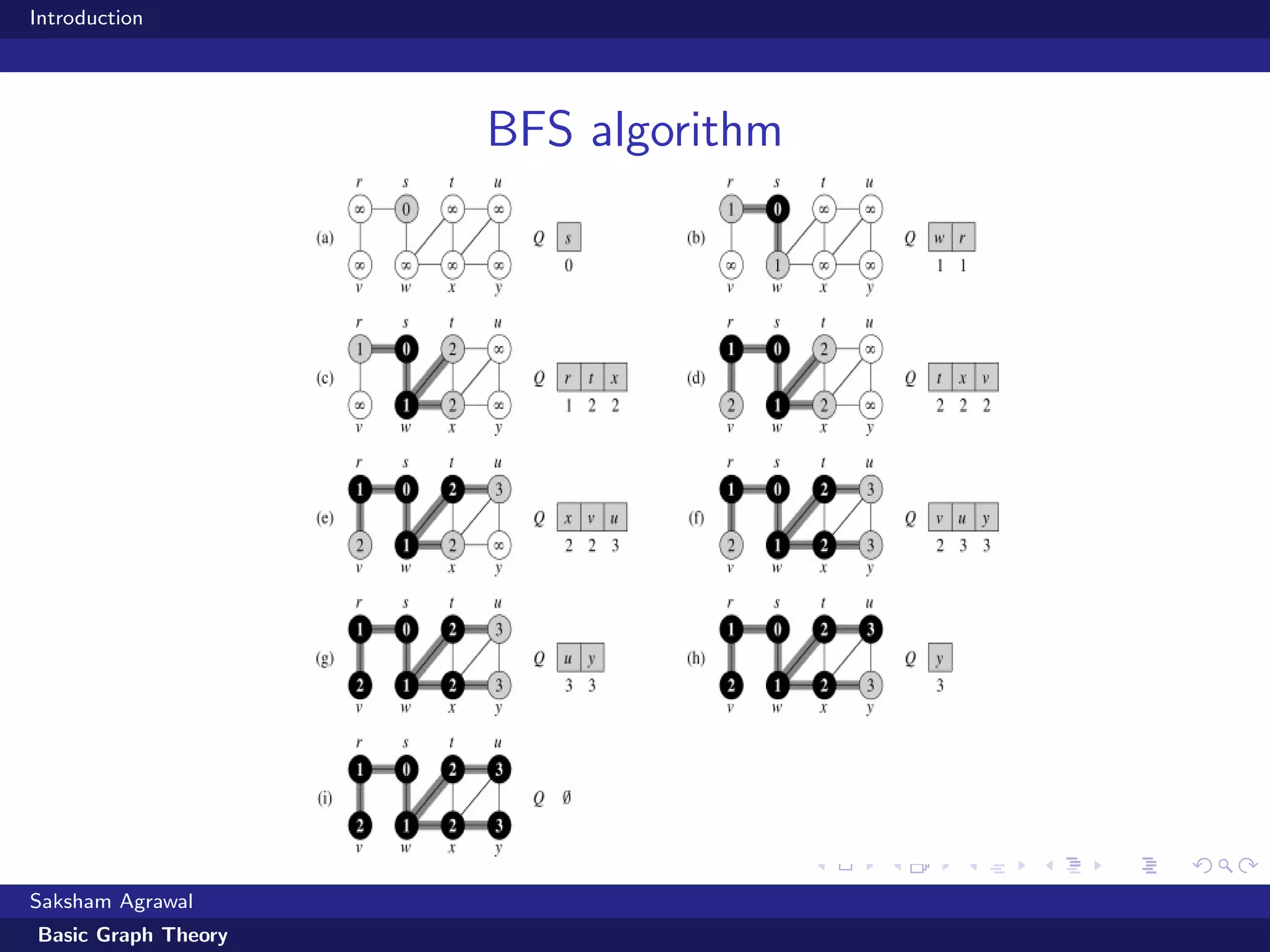
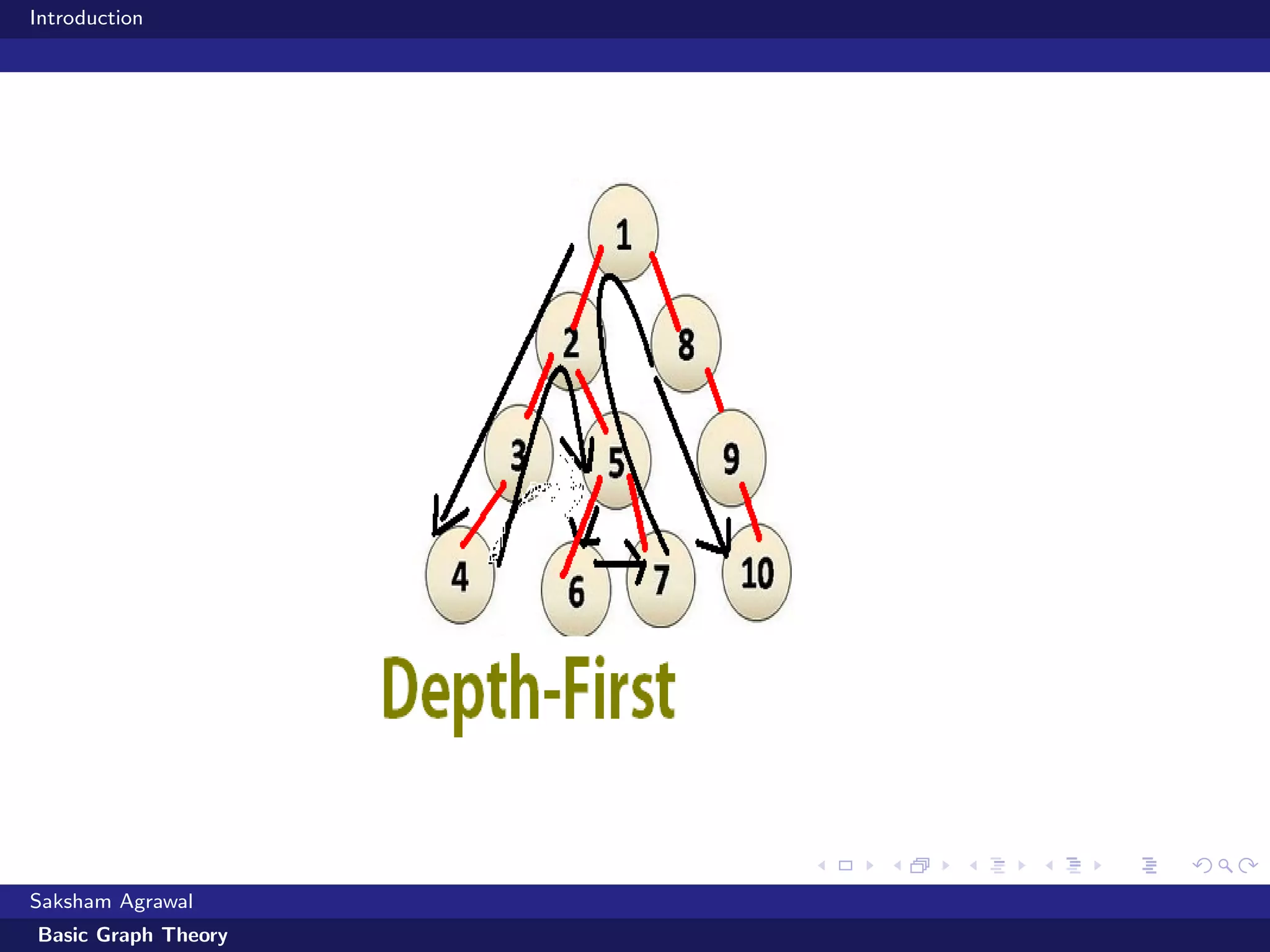
This document is an introduction to basic graph theory. It defines what a graph is made up of (vertices and edges) and describes different types of graphs (directed vs undirected). It also defines common graph terminology. The document outlines different ways to represent graphs using adjacency matrices and lists. It then describes algorithms for traversing graphs, including breadth-first search (BFS) and depth-first search (DFS), and provides examples of applications for each type of search.

1. Introduction
Basic Graph Theory
Saksham Agrawal
August 30, 2015
Saksham Agrawal
Basic Graph Theory

2. Introduction
List Of Contents
1- Introduction To Graph
2- Definitions And Terminology
3- Graph Representation
4- Breadth First Search
5- Depth first search
Saksham Agrawal
Basic Graph Theory

3. Introduction
Introduction To Graphs
In mathematics and computer science, graph theory is the
study of graphs, which are mathematical structures used to model
pairwise relations between objects. A ”graph” in this context is
made up of ”vertices” or ”nodes” and lines called edges that
connect them.
A graph may be undirected, meaning that there is no
distinction between the two vertices associated with each edge, or
its edges may be directed from one vertex to another. Graphs are
one of the prime objects of study in discrete mathematics.
Saksham Agrawal
Basic Graph Theory

4. Introduction
Figure: A Typical Graph
Saksham Agrawal
Basic Graph Theory

5. Introduction
Definitions And Terminology
Graphs are much clear when defined in mathematical terms. A
Graph G (V, E), consists of two sets,
Set of Vertices, V Set of Edges, E As the name suggest, V, is the
set of vertices or, the set of all nodes in a given graph and E, is the
set of all the edges between these nodes, or the associations
between them. So, V denotes the number of nodes in a graph and
E denotes the number of edges
Saksham Agrawal
Basic Graph Theory

6. Introduction
Figure: Types Of Graph
Saksham Agrawal
Basic Graph Theory

7. Introduction
Graph Representations ⇒
Adjacency Matrix
Adjacency List
Saksham Agrawal
Basic Graph Theory

8. Introduction
Adjacency Matrix
Figure: Adjacency Matrix Of Shown Graph
Saksham Agrawal
Basic Graph Theory

9. Introduction
Adjacency List
Figure: Adjacency List Of Shown Graph
Saksham Agrawal
Basic Graph Theory

10. Introduction
Breadth first Search
In BFS,we use a queue and we push the current vertex in the
queue and the vertices which are adjacent to the current vertex
using the adjacency list.We also maintain a visited array in which
we record the visited vertices so as to prevent revisiting the same
vertex.After we have pushed the adjacent vertices of a vertex we
pop it out of the queue.
Saksham Agrawal
Basic Graph Theory

11. Introduction
BFS algorithm
Saksham Agrawal
Basic Graph Theory

12. Introduction
Application of BFS
BFS is mainly used in a connected graph in which we want to find
the shortest path between 2 vertices.In this we also maintain a
level array.We start from one of the 2 vertices and set its level as 0
and the set level of the adjacent vertices as level of parent+1 and
traverse the graph in this until we reach the other vertex.The level
of the vertex represents the shortest path between the two vertices.
Saksham Agrawal
Basic Graph Theory

13. Introduction
Depth First Search
Algorithm:- When we see a maze in a newspaper or a magazine
or anywhere else, the way we solve it is we take a path and go
through it. If we find any junction or a crossroad, where we have a
choice of paths to choose, we mark that junction, take up a path
and traverse the whole route in your brain. If we see a dead end,
we realize that this leads we now where so we come back to the
junction we marked before and take up another path of the
junction. See if that is also a dead end, else we continue to explore
the, puzzle as this route contributes in reaching our destination.In
code, we do this by recursion.
Saksham Agrawal
Basic Graph Theory

14. Introduction
DFS step-by-step process
For a given set of vertices V = V1, V2,V3. . . , start with V1,
and explore all the vertices that can possibly be reached from V1.
Then go to the next vertex V2, if it hasn’t been visited, explore
all the nodes reachable from V2, if not, go for V3.
Similarly, go on picking up all the vertices one-by-one and
explore as much as possible if it wasn’t visited at all.
Saksham Agrawal
Basic Graph Theory

15. Introduction
Saksham Agrawal
Basic Graph Theory

16. Introduction
Application of DFS
DFS is also used for finding the shortest path between two
vertices.It is also used to do topological sorting.
Topological Sorting:-
It represents the logical order of doing
something. For instance,we wear socks before shoes and after we
tie laces.In the similar way in topological sorting a vertex appears
only when all its adjacent vertices have already appeared.It is
logical that topological sorting is done in only a directed
graph.Obviously, the vertex with no child is one which appears in
front.This is done using a stack and DFS on a graph.
Saksham Agrawal
Basic Graph Theory