Download to read offline
Uploaded byRomain Chion
Presentation Internship Brain Connectivity Graph 2014 (ENG)
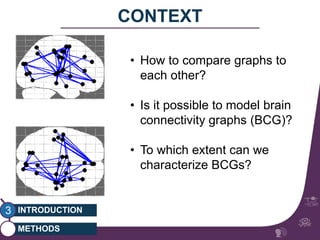
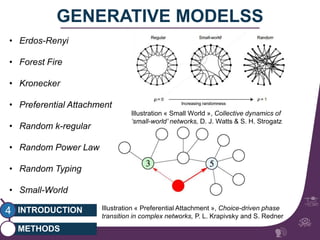
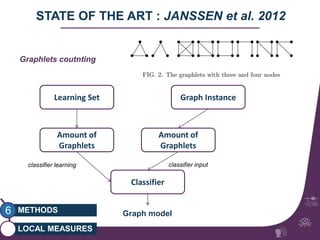
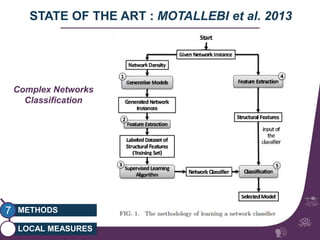
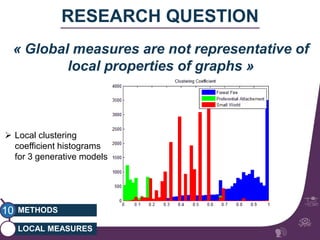
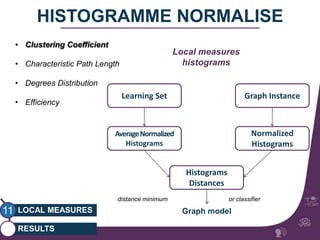
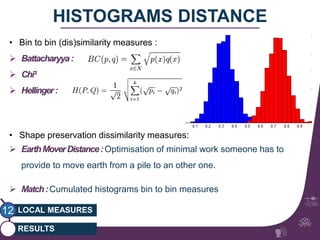
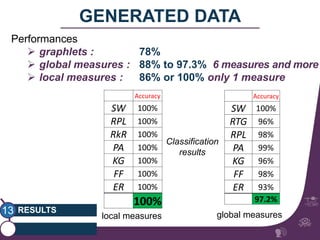
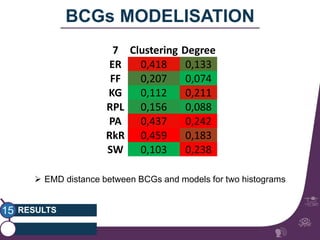
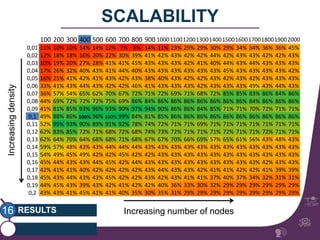
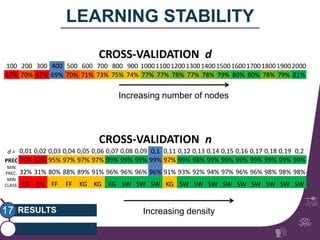
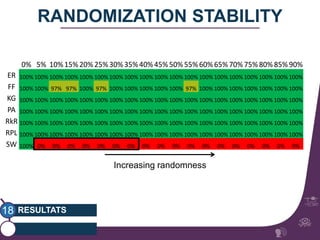
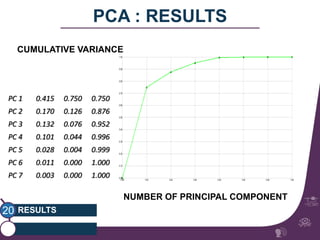
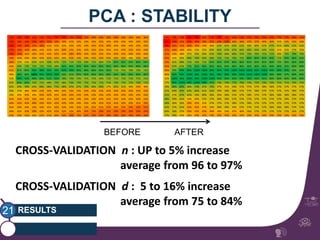
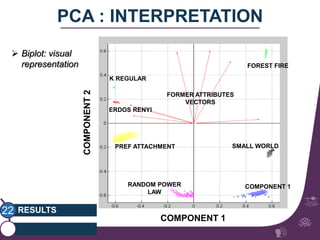
This document summarizes a study on classifying brain connectivity graphs (BCGs) using graph theory measures. It introduces graph theory concepts and previous work using global and local measures. The study finds that using histograms of local clustering coefficients and chi-squared distance achieves 83% accuracy classifying BCGs, outperforming global measures. It also examines the stability, scalability and effects of randomization on the classification approach.
Presentation Internship Brain Connectivity Graph 2014 (ENG)
- 1. « Brain ConnectivityGraph Classification » Romain Chion tutored by: S. Achard, M. Desvignes, F. Forbes, D. Vandeville
- 2. gipsa-lab SYNOPSIS INTRODUCTIONTO GRAPHS USUAL METHODS LOCAL MEASURES RESULTS
- 3. INTRODUCTION METHODS 3 gipsa-lab CONTEXT • How to compare graphs to each other? • Is it possible to model brain connectivity graphs (BCG)? • To which extent can we characterize BCGs?
- 4. INTRODUCTION METHODS 4 gipsa-lab GENERATIVE MODELSS Illustration « Small World », Collective dynamics of ‘small-world’ networks, D. J. Watts & S. H. Strogatz Illustration « Preferential Attachment », Choice-driven phase transition in complex networks, P. L. Krapivsky and S. Redner • Erdos-Renyi • Forest Fire • Kronecker • Preferential Attachment • Random k-regular • Random Power Law • Random Typing • Small-World
- 5. INTRODUCTION METHODS 5 gipsa-lab GRAPH COMPARISON • Transformation from a graph to another ex : Edition distance STRUCTURAL MEASURES • Nodes tendency to form clusters, degree distribution, path between nodes ex : Clustering, Characteristic Path Length LOCAL MEASURES (for each node) • Averagefor all local measures, coreand community formation ex : Assortativity, Centrality, Modularity,Diameter OVERALL MEASURES
- 6. STATE OF THEART : JANSSEN et al. 2012 Graphlets coutnting Amount of Graphlets classifier learning classifier input METHODS LOCAL MEASURES 6 gipsa-lab Learning Set Graph Instance Amount of Graphlets Classifier Graph model
- 7. STATE OF THEART : MOTALLEBI et al. 2013 Complex Networks Classification METHODS LOCAL MEASURES 7 gipsa-lab
- 8. Confidence interval ~25% METHODS LOCAL MEASURES 8 gipsa-lab BCGs MODELISATION BCGs classification in 4 generative models (Erdos-Renyi, Preferential Attachment, Random k-regular, Small-World) Classe Prédiction E-R P A R k-R S-W Control Small-World 0.2502 0.2501 0.2492 0.2505 Patient Small-World 0.2502 0.2501 0.2492 0.2505 Characterization with global measures and SVM classifier
- 9. Classification accuracy 50.16%,random at 50% METHODS LOCAL MEASURES 9 gipsa-lab BCGs IDENTIFICATION true Control true Patient class precision pred. Control 13 11 54.17% pred. Patient 7 6 46.15% class recall 65.00% 35.29% 50.16% Identification results with global measures and SVM classifier
- 10. METHODS LOCAL MEASURES gipsa-lab RESEARCH QUESTION « Global measures are not representative of local properties of graphs » Local clustering coefficient histograms for 3 generative models 10
- 11. HISTOGRAMME NORMALISE •Clustering Coefficient • Characteristic Path Length • Degrees Distribution • Efficiency LOCAL MEASURES RESULTS gipsa-lab Local measures histograms Learning Set Graph Instance AverageNormalized Histograms Histograms Distances Graph model Normalized Histograms distance minimum or classifier 11
- 12. • Bin tobin (dis)similarity measures : Battacharyya: Chi² Hellinger : • Shape preservation dissimilarity measures: EarthMoverDistance : Optimisation of minimal work someone has to LOCAL MEASURES RESULTS gipsa-lab HISTOGRAMS DISTANCE 12 provide to move earth from a pile to an other one. Match : Cumulated histograms bin to bin measures
- 13. Performances RESULTS gipsa-lab GENERATED DATA 13 graphlets : 78% global measures : 88% to 97.3% 6 measures and more local measures : 86% or 100% only 1 measure Accuracy SW 100% RPL 100% RkR 100% PA 100% KG 100% FF 100% ER 100% 100% Accuracy SW 100% RTG 96% RPL 98% PA 99% KG 96% FF 98% ER 93% 97.2% Classification results local measures global measures
- 14. MAX global measures63%V.S. 83%MAX histograms RESULTS gipsa-lab CONNECTIVITY GRAPHS 14 GLOBAL A.N.N. C P C 11 9 55% P 5 12 71% 69% 57% 63% HISTOGRAM CLUSTERING AND CHI² C P C 18 2 90% P 4 13 76% 82% 87% 83% Confusion matrix of Control / Patient identification
- 15. RESULTS gipsa-lab BCGsMODELISATION 15 7 Clustering Degree ER 0,418 0,133 FF 0,207 0,074 KG 0,112 0,211 RPL 0,156 0,088 PA 0,437 0,242 RkR 0,459 0,183 SW 0,103 0,238 EMD distance between BCGs and models for two histograms
- 16. RESULTS gipsa-lab SCALABILITY 16 100 200 300 400 500 600 700 800 900 10001100120013001400150016001700180019002000 0,01 11% 10% 10% 14% 14% 12% 7% 6% 14% 11% 23% 29% 29% 30% 29% 34% 34% 36% 36% 45% 0,02 12% 18% 18% 16% 20% 22% 30% 39% 41% 42% 43% 42% 42% 44% 42% 43% 43% 42% 42% 43% 0,03 10% 19% 20% 27% 28% 41% 41% 45% 43% 43% 43% 42% 41% 40% 44% 43% 44% 43% 43% 43% 0,04 17% 26% 32% 40% 43% 41% 44% 40% 43% 43% 43% 43% 43% 43% 45% 43% 43% 43% 43% 42% 0,05 16% 25% 41% 42% 41% 43% 42% 43% 38% 40% 43% 42% 42% 43% 42% 43% 42% 43% 43% 43% 0,06 33% 41% 43% 44% 43% 42% 42% 46% 41% 43% 43% 43% 42% 43% 43% 43% 49% 43% 44% 43% 0,07 36% 57% 54% 65% 62% 70% 67% 72% 71% 72% 69% 71% 68% 72% 85% 85% 83% 86% 84% 86% 0,08 44% 69% 72% 72% 72% 75% 69% 86% 84% 86% 86% 86% 86% 86% 86% 86% 84% 86% 86% 86% 0,09 41% 81% 85% 93% 96% 93% 90% 97% 94% 90% 86% 86% 84% 85% 71% 71% 70% 72% 71% 71% 0,1 49% 88% 86% 100% 96% 100% 99% 84% 81% 85% 86% 86% 86% 86% 86% 86% 86% 86% 86% 86% 0,11 52% 99% 93% 90% 89% 91% 92% 78% 74% 72% 71% 71% 69% 71% 71% 71% 71% 71% 71% 71% 0,12 62% 83% 85% 72% 71% 68% 72% 68% 74% 73% 72% 71% 71% 71% 72% 71% 71% 72% 71% 71% 0,13 62% 64% 70% 64% 68% 68% 71% 68% 67% 67% 70% 66% 69% 57% 65% 61% 56% 43% 48% 43% 0,14 59% 57% 48% 43% 43% 44% 44% 44% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 0,15 54% 49% 45% 49% 42% 42% 45% 42% 42% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 0,16 45% 44% 43% 43% 44% 45% 42% 44% 43% 43% 43% 43% 43% 43% 43% 43% 43% 42% 43% 43% 0,17 42% 41% 41% 40% 42% 42% 42% 42% 43% 44% 43% 43% 42% 41% 41% 42% 42% 41% 39% 39% 0,18 45% 43% 44% 43% 43% 45% 42% 42% 43% 42% 43% 41% 41% 37% 40% 37% 34% 32% 31% 31% 0,19 44% 45% 43% 39% 43% 42% 41% 42% 42% 40% 36% 33% 30% 32% 29% 29% 29% 29% 29% 29% 0,2 43% 43% 41% 45% 41% 41% 40% 35% 30% 35% 31% 29% 29% 29% 29% 29% 29% 29% 29% 29% Increasing number of nodes Increasing density
- 17. RESULTS gipsa-lab LEARNINGSTABILITY 17 CROSS-VALIDATION d 100 200 300 400 500 600 700 800 900 10001100120013001400150016001700180019002000 67% 70% 67% 69% 70% 71% 73% 75% 74% 77% 77% 78% 77% 78% 79% 80% 80% 78% 79% 81% Increasing number of nodes CROSS-VALIDATION n d = 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 PREC 76% 82% 95% 97% 97% 97% 99% 99% 99% 99% 97% 99% 98% 99% 99% 99% 99% 99% 99% 99% MIN PREC. 32% 31% 80% 88% 89% 91% 96% 96% 96% 96% 91% 93% 92% 94% 97% 96% 96% 98% 98% 98% MIN CLASS. ER ER FF FF KG KG KG SW SW SW KG SW SW SW SW SW SW SW SW SW Increasing density
- 18. RANDOMIZATION STABILITY 0%5% 10%15%20%25%30%35%40%45%50%55%60%65%70%75%80%85%90% ER 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% FF 100% 100% 97% 97% 100% 97% 100% 100% 100% 100% 100% 97% 100% 100% 100% 100% 100% 100% 100% KG 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% PA 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% RkR 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% RPL 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% 100% SW 100% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% 0% RESULTATS 18 gipsa-lab Increasing randomness
- 19. Erdos- Renyi FF RPL RESULTS gipsa-lab REMOVING CLASSES 19 Forest Fire RPL SW Kronecker Graph FF 77%SW 23%RPL Preferential Attachment FF RPL Random k-Regular FF RPL Random Power Law FF 92% SW 8% PA Small- World FF RPL Graphes de Connectivités FF RPL PA SW …
- 20. PC 1 0.4150.750 0.750 PC 2 0.170 0.126 0.876 PC 3 0.132 0.076 0.952 PC 4 0.101 0.044 0.996 PC 5 0.028 0.004 0.999 PC 6 0.011 0.000 1.000 PC 7 0.003 0.000 1.000 RESULTS gipsa-lab PCA : RESULTS 20 NUMBER OF PRINCIPAL COMPONENT CUMULATIVE VARIANCE
- 21. BEFORE AFTER CROSS-VALIDATIONn : UP to 5% increase RESULTS gipsa-lab PCA : STABILITY 21 14% 14% 14% 2% 0% 20% 11% 5% 14% 15% 14% 15% 15% 15% 15% 17% 17% 20% 23% 1% 14% 25% 15% 20% 28% 25% 24% 19% 36% 36% 37% 37% 40% 40% 55% 43% 42% 43% 6% 26% 31% 30% 35% 43% 46% 63% 62% 64% 63% 58% 60% 61% 67% 61% 66% 63% 61% 27% 34% 42% 45% 53% 55% 60% 66% 67% 67% 66% 68% 66% 64% 63% 51% 55% 57% 55% 31% 43% 48% 57% 59% 60% 63% 70% 66% 69% 71% 70% 70% 71% 71% 58% 70% 78% 70% 32% 51% 56% 69% 70% 66% 68% 72% 71% 74% 72% 86% 86% 85% 84% 71% 85% 86% 83% 34% 62% 68% 71% 70% 71% 83% 86% 87% 86% 86% 85% 84% 85% 86% 79% 84% 86% 86% 36% 67% 67% 79% 85% 86% 86% 86% 84% 86% 86% 86% 86% 86% 86% 86% 85% 86% 86% 40% 76% 94% 99% 100% 100% 98% 99% 99% 100% 100% 100% 99% 100% 94% 96% 96% 83% 82% 46% 96% 99% 100% 98% 100% 99% 98% 98% 98% 100% 100% 100% 100% 88% 88% 87% 88% 86% 52% 100% 96% 100% 99% 100% 100% 95% 94% 92% 93% 96% 92% 91% 86% 86% 86% 86% 86% 57% 98% 100% 99% 100% 98% 87% 73% 74% 77% 75% 72% 72% 73% 72% 71% 71% 72% 71% 58% 80% 85% 68% 73% 67% 70% 57% 55% 59% 57% 57% 57% 58% 58% 57% 57% 57% 57% 61% 64% 69% 64% 66% 61% 63% 59% 58% 58% 57% 57% 58% 57% 57% 57% 57% 58% 57% 65% 57% 67% 62% 59% 60% 58% 56% 58% 57% 57% 58% 57% 57% 58% 58% 58% 58% 57% 68% 59% 61% 53% 56% 57% 57% 58% 58% 57% 57% 57% 57% 57% 57% 57% 58% 57% 57% 66% 56% 56% 42% 45% 52% 57% 57% 57% 58% 57% 58% 57% 57% 57% 57% 57% 57% 57% 62% 57% 61% 43% 43% 47% 54% 58% 58% 55% 57% 57% 57% 57% 58% 58% 58% 57% 57% 60% 58% 57% 43% 43% 43% 44% 49% 54% 47% 46% 56% 57% 57% 57% 57% 57% 56% 57% 57% 59% 52% 46% 43% 42% 43% 42% 41% 43% 44% 43% 43% 43% 43% 43% 43% 43% 43% 11% 10% 10% 14% 14% 12% 7% 6% 14% 11% 23% 29% 29% 30% 29% 34% 34% 36% 36% 12% 18% 18% 16% 20% 22% 30% 39% 41% 42% 43% 42% 42% 44% 42% 43% 43% 42% 42% 10% 19% 20% 27% 28% 41% 41% 45% 43% 43% 43% 42% 41% 40% 44% 43% 44% 43% 43% 17% 26% 32% 40% 43% 41% 44% 40% 43% 43% 43% 43% 43% 43% 45% 43% 43% 43% 43% 16% 25% 41% 42% 41% 43% 42% 43% 38% 40% 43% 42% 42% 43% 42% 43% 42% 43% 43% 33% 41% 43% 44% 43% 42% 42% 46% 41% 43% 43% 43% 42% 43% 43% 43% 49% 43% 44% 36% 57% 54% 65% 62% 70% 67% 72% 71% 72% 69% 71% 68% 72% 85% 85% 83% 86% 84% 44% 69% 72% 72% 72% 75% 69% 86% 84% 86% 86% 86% 86% 86% 86% 86% 84% 86% 86% 41% 81% 85% 93% 96% 93% 90% 97% 94% 90% 86% 86% 84% 85% 71% 71% 70% 72% 71% 49% 88% 86% 100% 96% 100% 99% 84% 81% 85% 86% 86% 86% 86% 86% 86% 86% 86% 86% 52% 99% 93% 90% 89% 91% 92% 78% 74% 72% 71% 71% 69% 71% 71% 71% 71% 71% 71% 62% 83% 85% 72% 71% 68% 72% 68% 74% 73% 72% 71% 71% 71% 72% 71% 71% 72% 71% 62% 64% 70% 64% 68% 68% 71% 68% 67% 67% 70% 66% 69% 57% 65% 61% 56% 43% 48% 59% 57% 48% 43% 43% 44% 44% 44% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 54% 49% 45% 49% 42% 42% 45% 42% 42% 43% 43% 43% 43% 43% 43% 43% 43% 43% 43% 45% 44% 43% 43% 44% 45% 42% 44% 43% 43% 43% 43% 43% 43% 43% 43% 43% 42% 43% 42% 41% 41% 40% 42% 42% 42% 42% 43% 44% 43% 43% 42% 41% 41% 42% 42% 41% 39% 45% 43% 44% 43% 43% 45% 42% 42% 43% 42% 43% 41% 41% 37% 40% 37% 34% 32% 31% 44% 45% 43% 39% 43% 42% 41% 42% 42% 40% 36% 33% 30% 32% 29% 29% 29% 29% 29% 43% 43% 41% 45% 41% 41% 40% 35% 30% 35% 31% 29% 29% 29% 29% 29% 29% 29% 29% average from 96 to 97% CROSS-VALIDATION d : 5 to 16% increase average from 75 to 84%
- 22. RESULTS gipsa-lab PCA: INTERPRETATION 22 COMPONENT 2 FORMER ATTRIBUTES COMPONENT 1 Biplot: visual representation K REGULAR ERDOS RENYI RANDOM POWER LAW FOREST FIRE SMALL WORLD COMPONENT 1 PREF ATTACHMENT VECTORS
- 23. gipsa-lab CONCLUSION Excellent performances on generated data Histograms of local measures are useful Local clustering is particularly important Still dependent on existing and number of models Results on connectivity data are still lacking Combined model are to be considered Basis of histograms to be constructed
Editor's Notes
- #2 Bonjour à tous Je vais vous présenter mes travaux sur les graphes, et plus particulièrement sur la classif…erveau issue de mon stage ici au GIPSA lab
- #3 Après une rapide présentation du contexte je vais vous présenter deux méthodes usuelles issues de la littérature avant d’introduire les concepts de mesures locales et d‘histogrammes et enfin une comparaison des résultats et des performances.
- #4 Dans cette étude nous cherchons à comparer des graphes entre eux. Vous avez ici l’exemples de Graphes de Connectivité du Cerveau avec les nœuds en noirs, et les arêtes en bleu, on les obtient par imagerie IRM sur des personnes saines agissant comme control et sur des patients atteints de troubles psychologiques ou neurologiques comme un comma. On sépare alors le cerveau en différentes régions représentées chacune par un nœud. Une arête montrant un lien fonctionnel entre deux régions. Ces GCC constituent nos données réelles, nous allons pouvoir les comparer par la suite à des graphes de synthèses pour en définir un modèle. VISUEL GRAPH CONNECTIVITE -> COMMENT CARACTERISER LES GRAPHES LES UNS AU AUTRES / MODELISER ELS DONNEES REELES PAR UNE (DES) METHODES GENERATIVES / CATEGORISER LES DONNEES REELLES ENTRES ELLES.
- #5 Les modèles génératifs présentent différentes manières de générer des graphes. Tous ces modèles sont simulés d’après plusieurs paramètres comme leur nombre de noeuds et d’arêtes. Vous avez ici une autre représentation visuelle des graphes où les noeuds sont répartis sur un cercle. Trois modèles peuvent êtres définis comme présentés ici, le modèle régulier ou tous les nœuds sont liés à leurs k plus proches voisins. On va pouvoir ensuite reconnecter aléatoirement les arêtes avec une probabilité p jusqu’à atteindre le modèle dit Small-World Si on continue encore on va obtenir un modèle complètement aléatoire ou modèle Erdos Renyi. Un autre modèle initié par Barabasi est le Préférential Attachment, l’idée représentée ici est qu’il est plus probable de trouver de nouveaux amis chez les amis de mes amis que chez des personnes avec lesquelles je n’ai aucune relation. Le Préférential attachement modèlise parfaitement les réseaux sociaux ou encore le système de citation dans les articles.
- #6 Maintenant que nous avons plusieurs types de graphes nous allons chercher à les comparer. Pour cela il existe plusieurs types de mesures heavy tailed degree distribution, high clustering, small path length
- #7 Nous allons maintenant entrer dans le vif du sujet avec une première méthode de classification de graphes basé sur le comptage de motifs appelés GRAPHLETS On peut voir ici les différents motifs pour 3 et 4 nœuds. On commence par compter le nombre de graphlets d’un ensemble d’apprentissage composés d’un certain nombre de graphes pour chaque modèle étudié ont on va se servir pour créer un classifieur. Pour chaque nouvelle instance de graphe à tester on va
- #8 Classifieur adapté au graph en entrée et on cherche une indépendance vis-à-vis du nombre de noeud
- #9 On a donc commencé par essayer de repartir les graphes de connectivites selon differents modeles generatifs pour voir s’il y en a un qui colle. Pour cela on a utilisé les mesures globales d’une centaine de graphes pour 4 modeles generatifs comme ensemble d’apprentissage et on a ensuite passé les 37 GCC dans un classifieur SVM. Prédiction basée sur le max pas de sens, même données autres classifieurs autres modèles. 25% partout, ces 4 modèles de synthèses avec les paramètres, ne permettent pas de caractériser les données réelles, pas adéquat, pas discriminant, le graph n’est pas reconnu Patient comme Control
- #10 Inspiration pour classifier les PATIENT/CONTROL en cross valiation/leave one out avec un classifieur SVM, on voit bien qu’on est incapable de les séparer avec mesures globales.
- #11 RESULTATS mitigés, en simulation avec graphes de synthèses seuls, comme ce qu’on voit dans la littérature, ça marche bien mais... Faiblesse des méthodes précédentes. PBMTK -> Intérêt des mesures locales, un histogramme pour illustrer,
- #12 FORTEMENT INSPIRE DE LA DEUXIEME METHODE APPRENTISSAGE 7 modèles génératifs Un histogramme moyen pour chaque modèle Plus petit / apprentissage NORMALISE / MOYENS Mesures locales, les histogrammes moyens
- #13 2 histogrammes de graphes <> 5 distances, sens physique (pas de divergence car elles nécessitent un support commun)
- #14 1 seule mesure (Clustering) Expliquer le process + METHODE DE S. MOTALLEBI
- #24 Pourquoi pas fitter des lois ? On ne peut pas toujours au vu de la forme des histogrammes. Pourquoi pas directement un histogramme dans le classifieur ? Pas vraiment de sens, 30 mesures, un énorme nombre d’échantillons Regarder histo Kro/SW