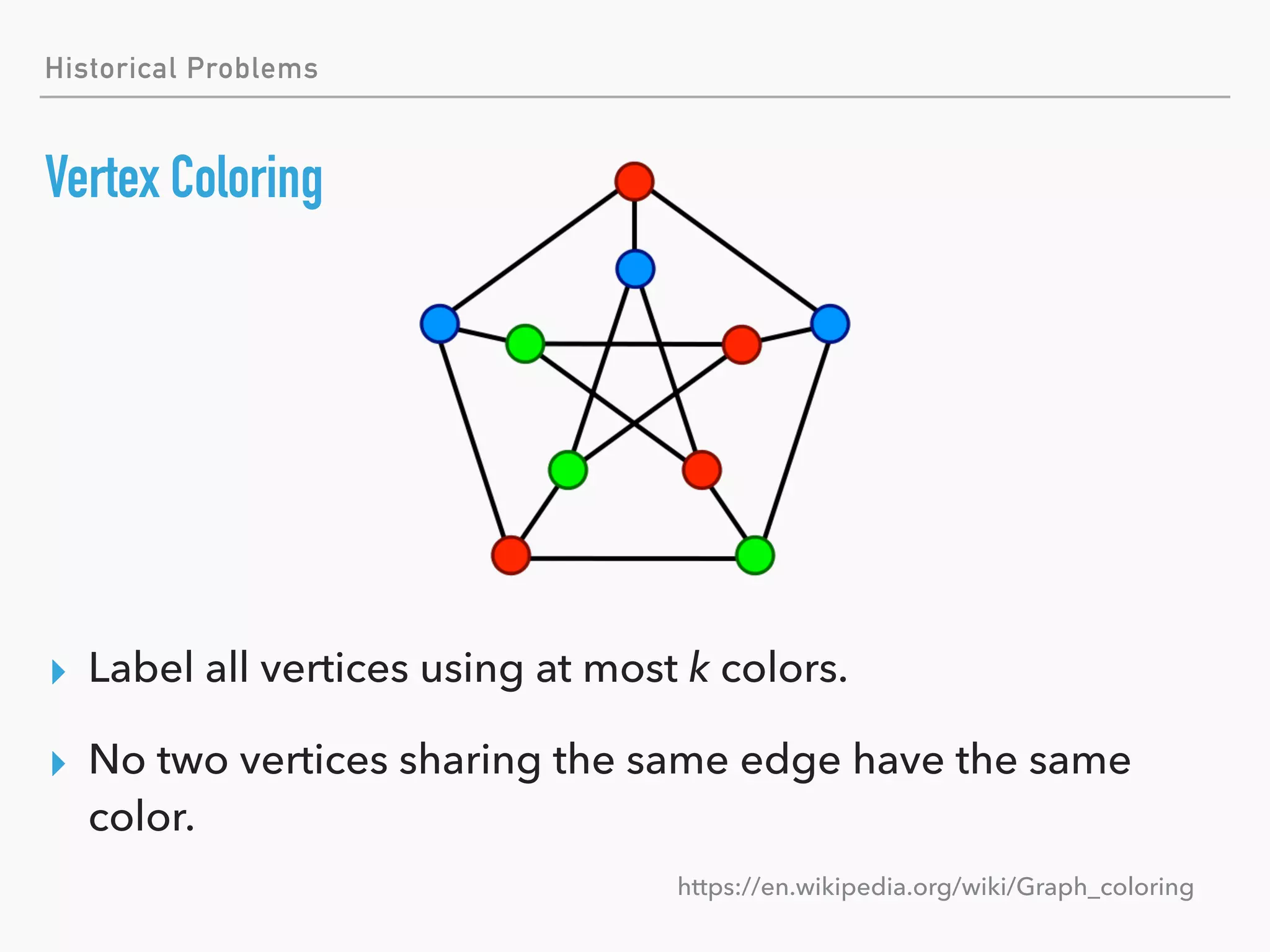
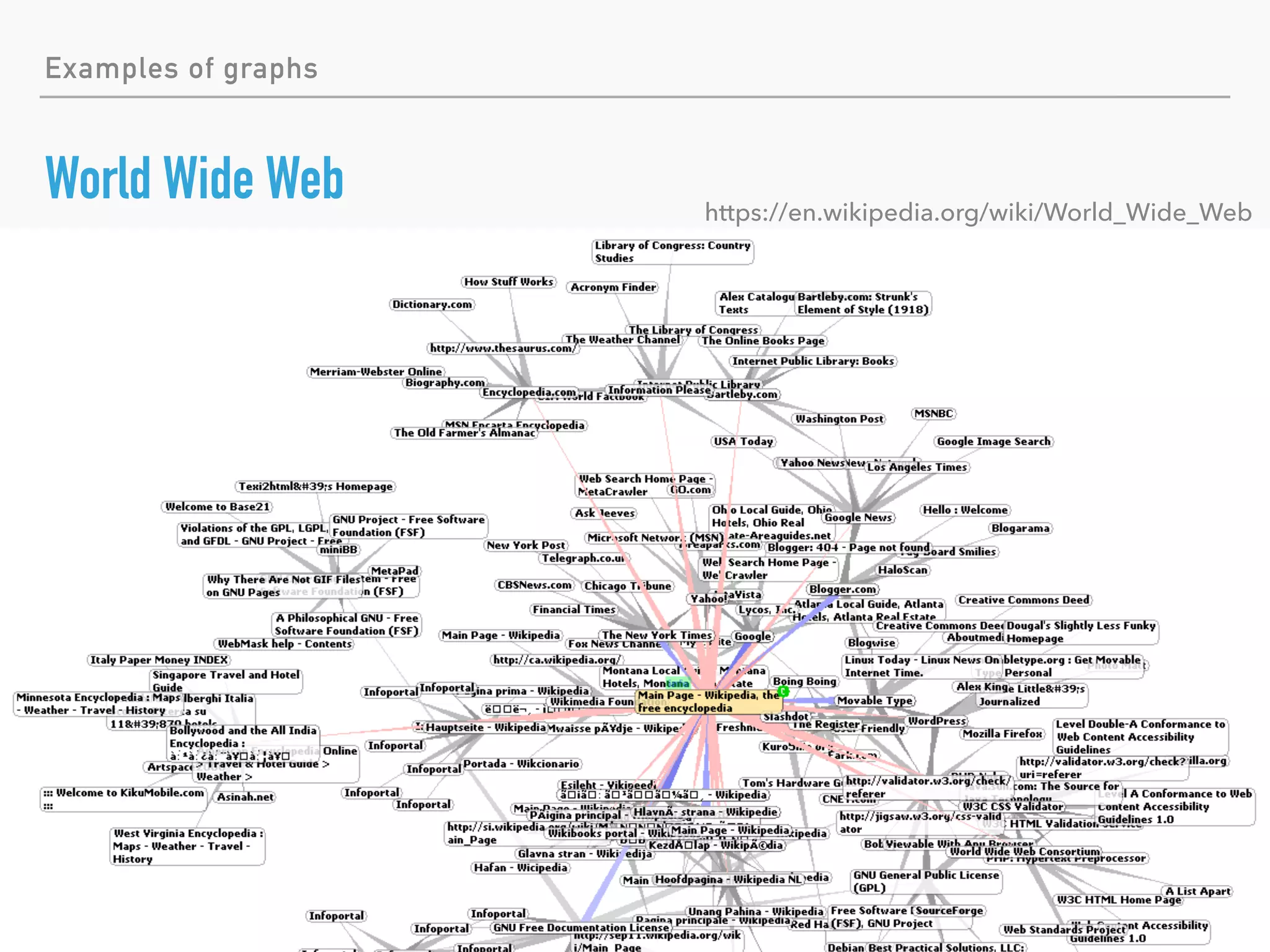
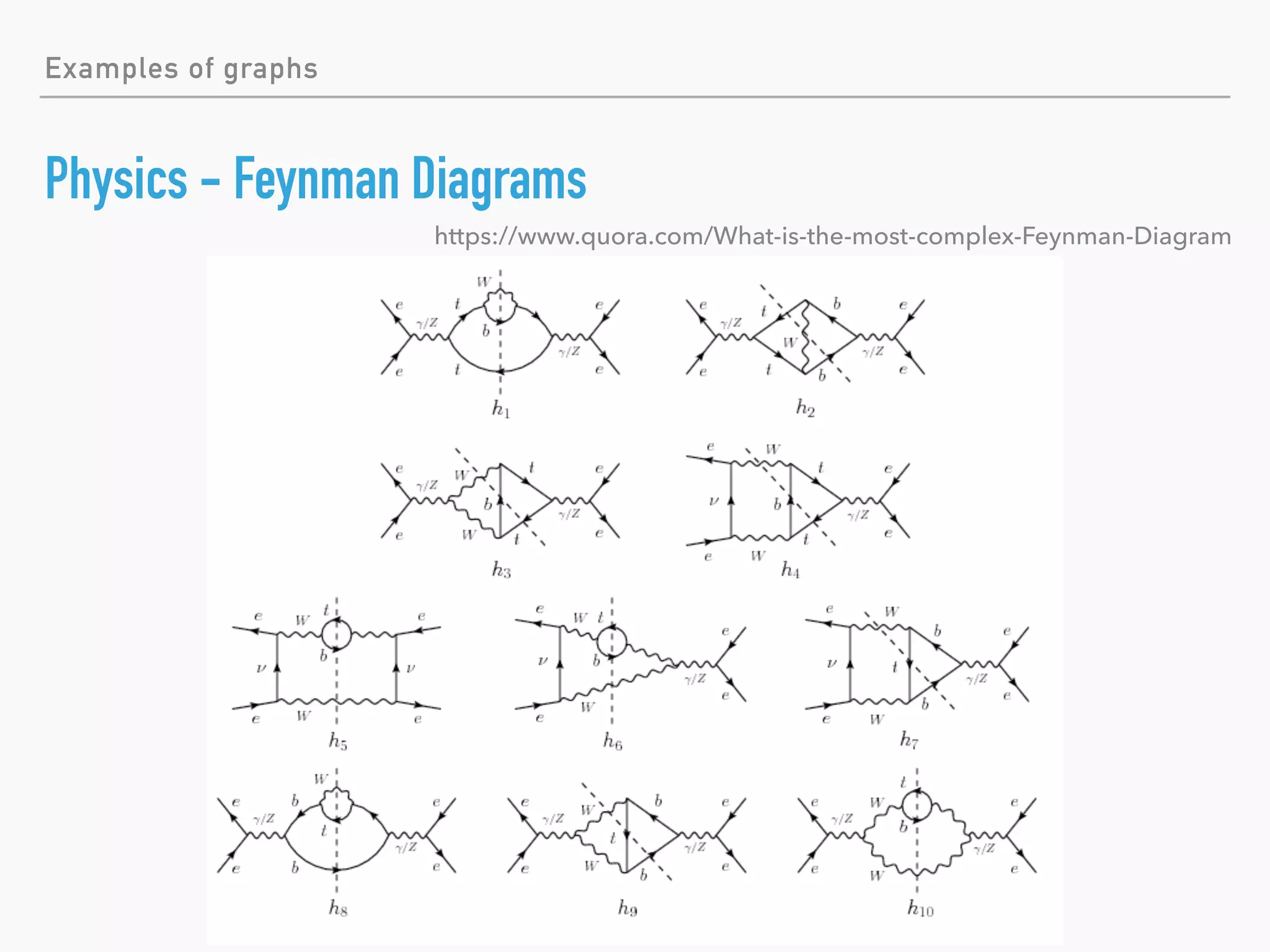
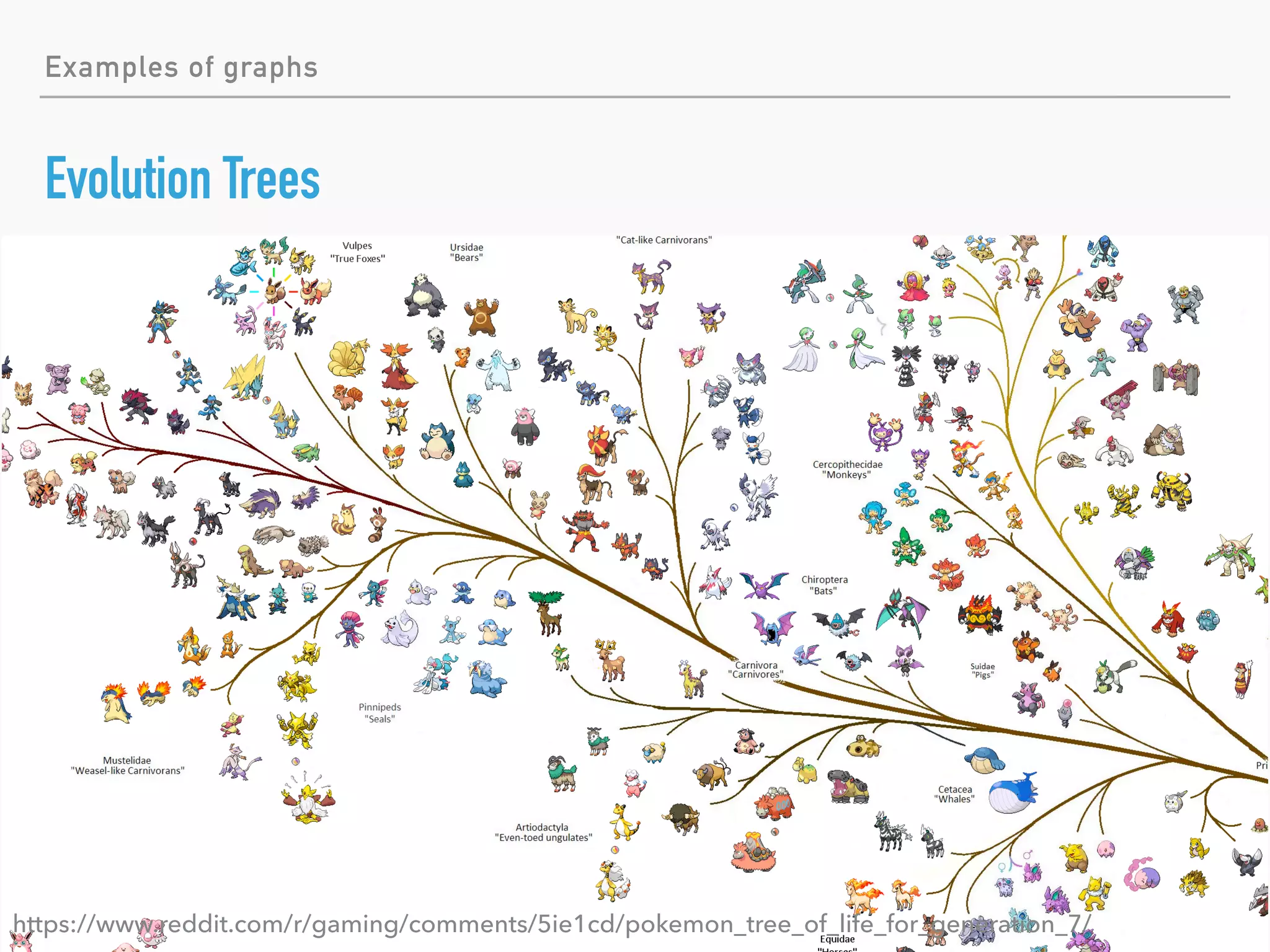
This document introduces the topic of graph theory. It defines what graphs are, including vertices, edges, directed and undirected graphs. It provides examples of graphs like social networks, transportation maps, and more. It covers basic graph terminology such as degree, regular graphs, subgraphs, walks, paths and cycles. It also discusses graph classes like trees, complete graphs and bipartite graphs. Finally, it touches on some historical graph problems, complexity analysis, centrality analysis, facility location problems and applications of graph theory.



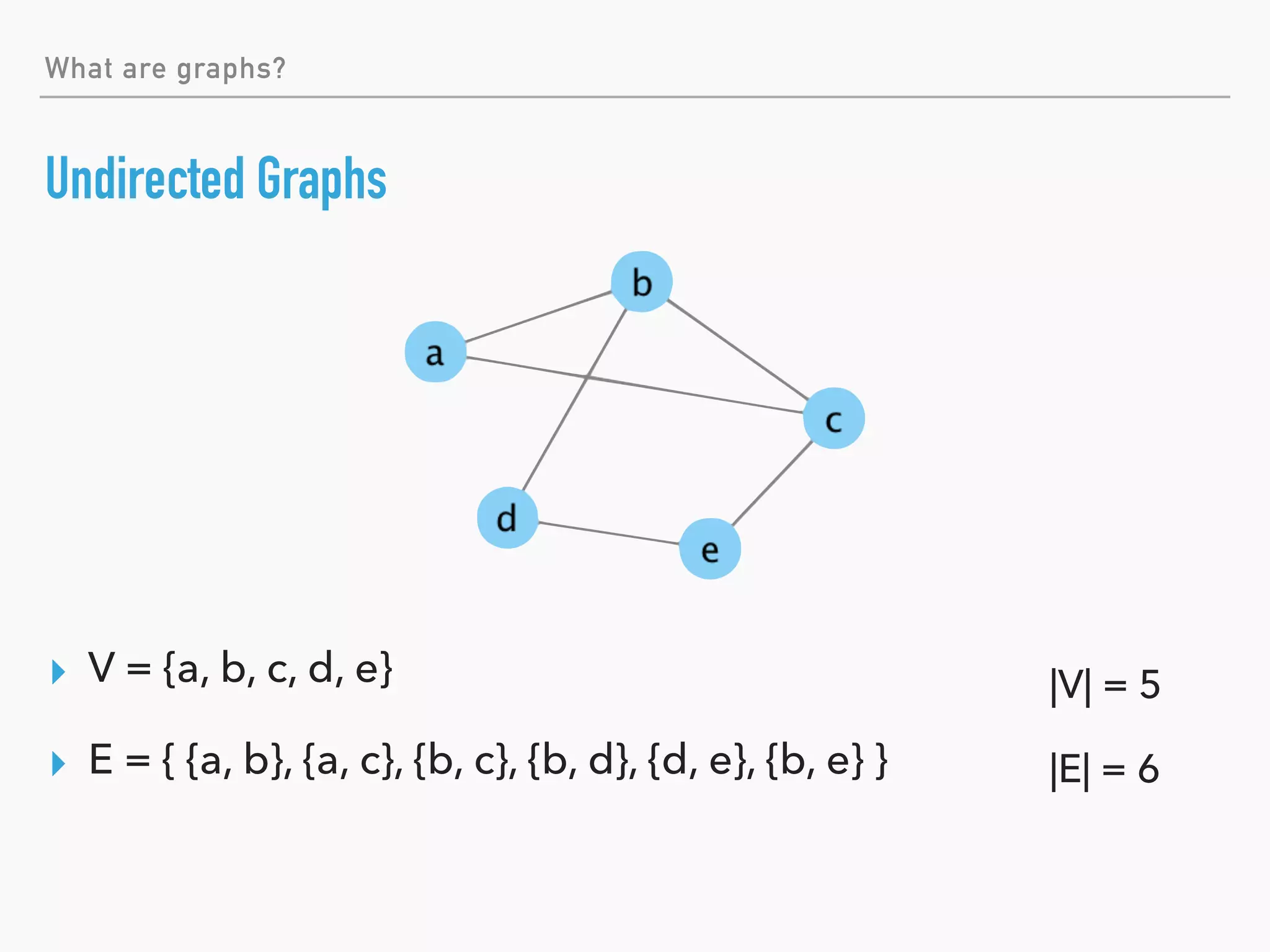















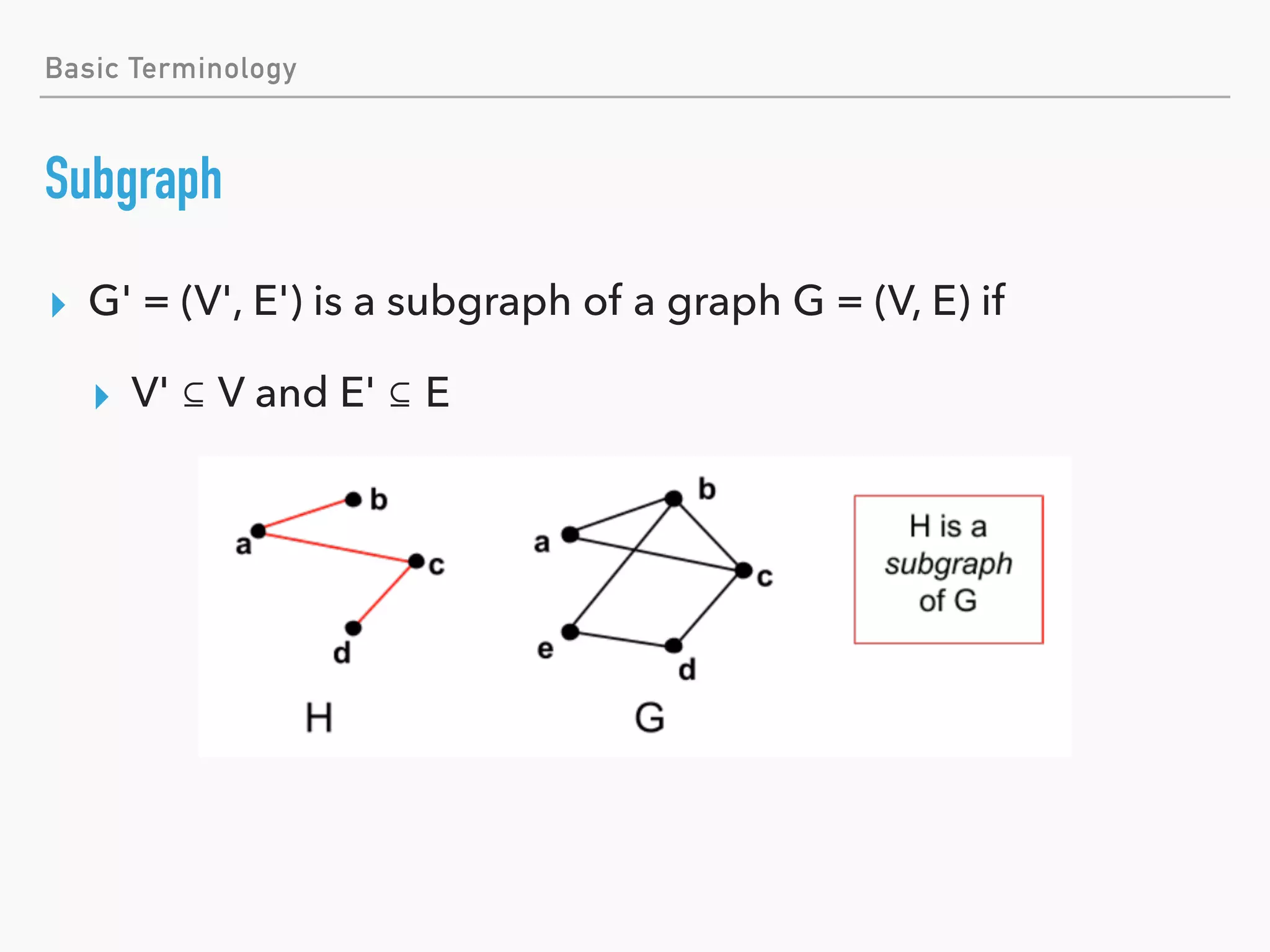
![Basic Terminology
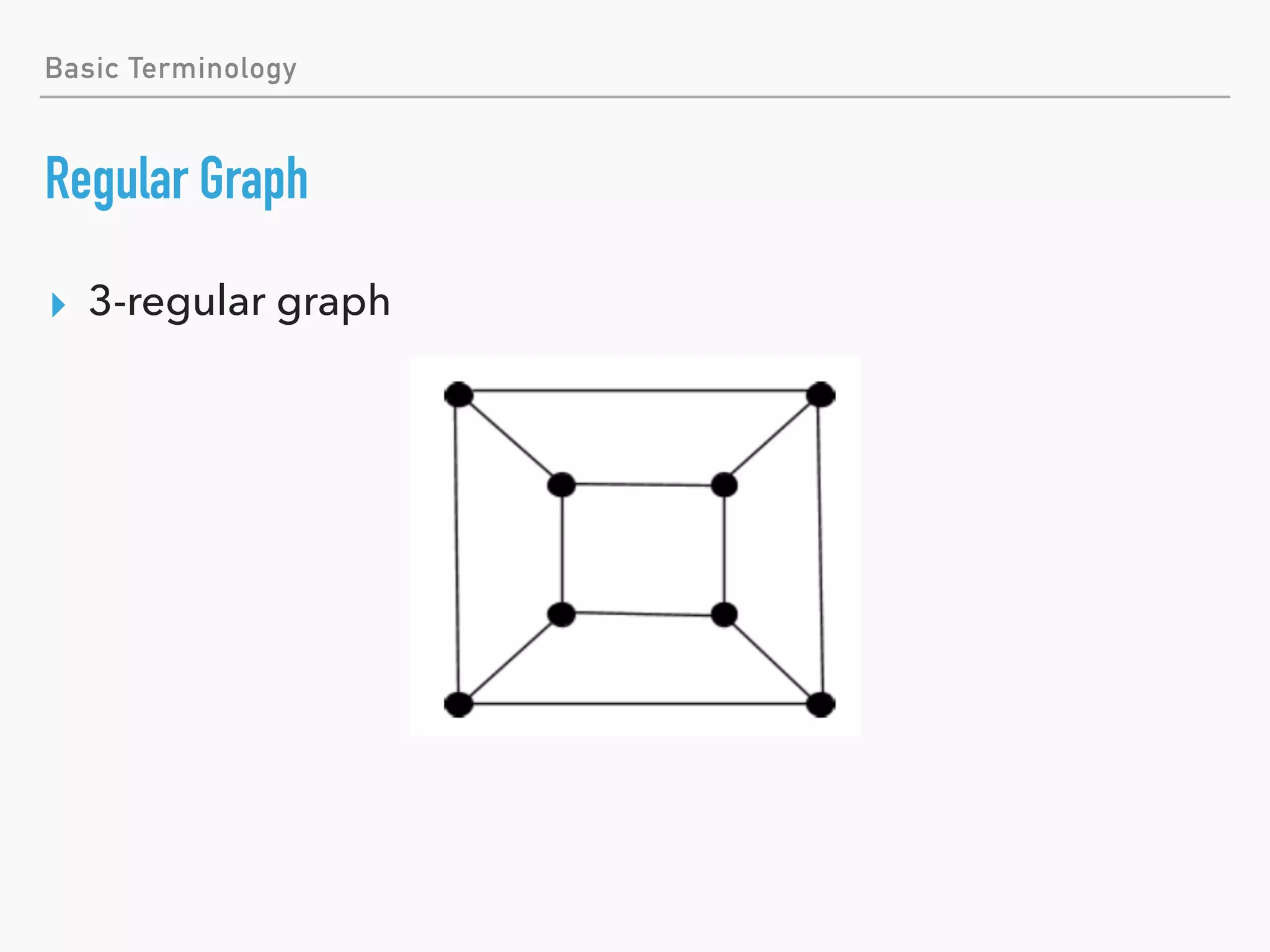
Regular Graph
▸ All the vertices have the same degree.
▸ D-regular graph:
▸ All the vertices have degree d.
▸ [Question] Draw a 3-regular undirected graph
with 8 vertices.](https://image.slidesharecdn.com/introductiontographtheoryskip-180922053843/75/Introduction-to-Graph-Theory-25-2048.jpg)

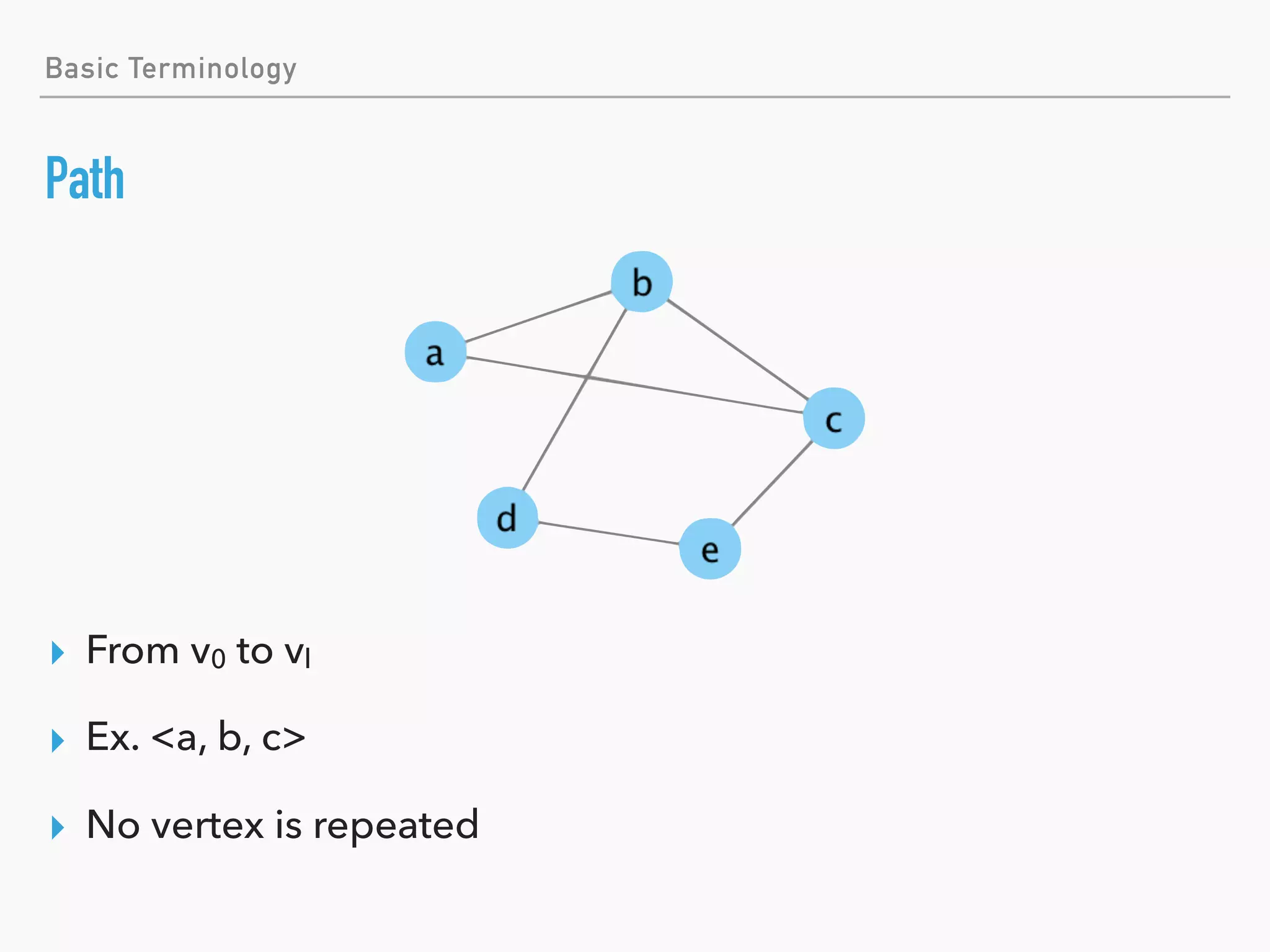


![Basic Terminology
[Question] Walk / Path / Circuit / Cycle?
▸ 1) <a, b, a>
▸ 2) <a, b, d, e, c>
▸ 3) <a, b, d, e, c, b>
▸ 4) <a, b, d, e, c, a>](https://image.slidesharecdn.com/introductiontographtheoryskip-180922053843/75/Introduction-to-Graph-Theory-32-2048.jpg)



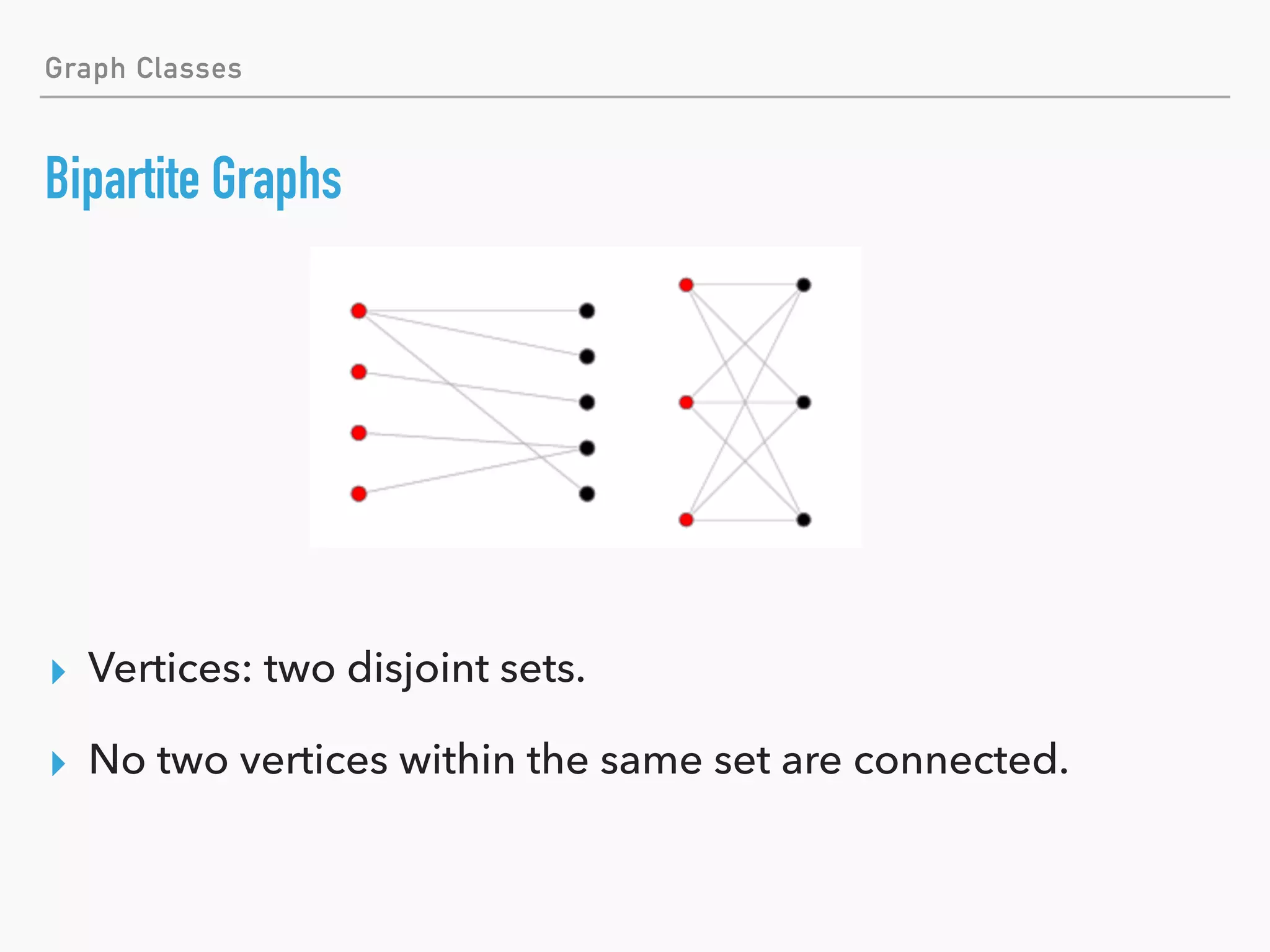
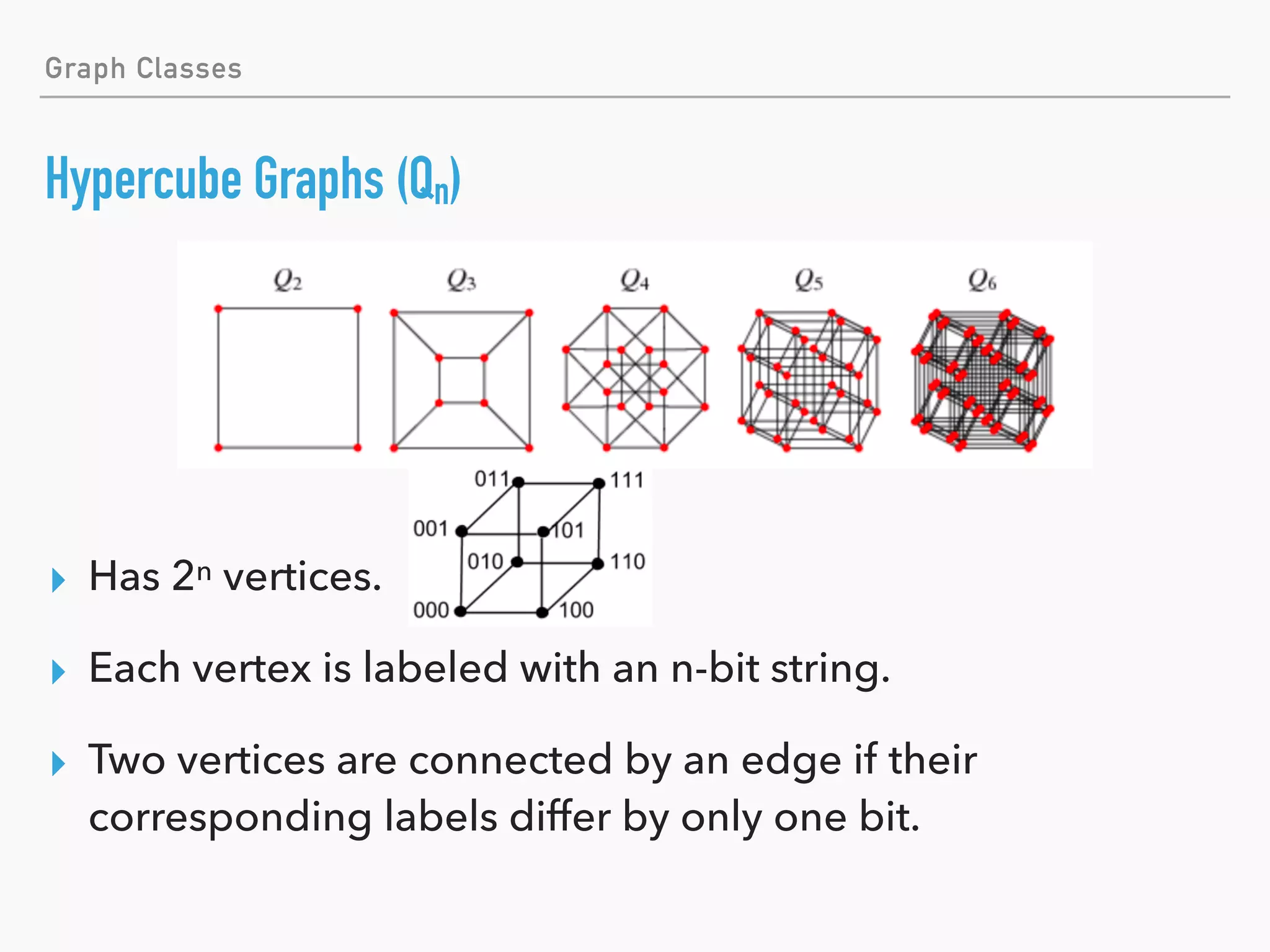
![Graph Classes
Complete Graphs (Kn)
▸ Each vertex pair is connected by an edge.
▸ [Question] How many edges does Kn have?](https://image.slidesharecdn.com/introductiontographtheoryskip-180922053843/75/Introduction-to-Graph-Theory-36-2048.jpg)




![Historical Problems
Eulerian Trail (Eulerian Path)
▸ [Question] Find an Eulerian trail.
▸ There are effective algorithms to construct Eulerian trais.
▸ Fleury's algorithm (1883)
▸ Hierholzer's algorithm (1873)
https://courses.lumenlearning.com/wmopen-mathforliberalarts/chapter/introduction-euler-paths/](https://image.slidesharecdn.com/introductiontographtheoryskip-180922053843/75/Introduction-to-Graph-Theory-44-2048.jpg)
![Historical Problems
Hamiltonian Path / Cycle
▸ Path / cycle which visits every vertex exactly once.
▸ No effective algorithm to construct Hamiltonian paths.
▸ [Question] Draw a graph that does not have any Hamiltonian paths.](https://image.slidesharecdn.com/introductiontographtheoryskip-180922053843/75/Introduction-to-Graph-Theory-45-2048.jpg)