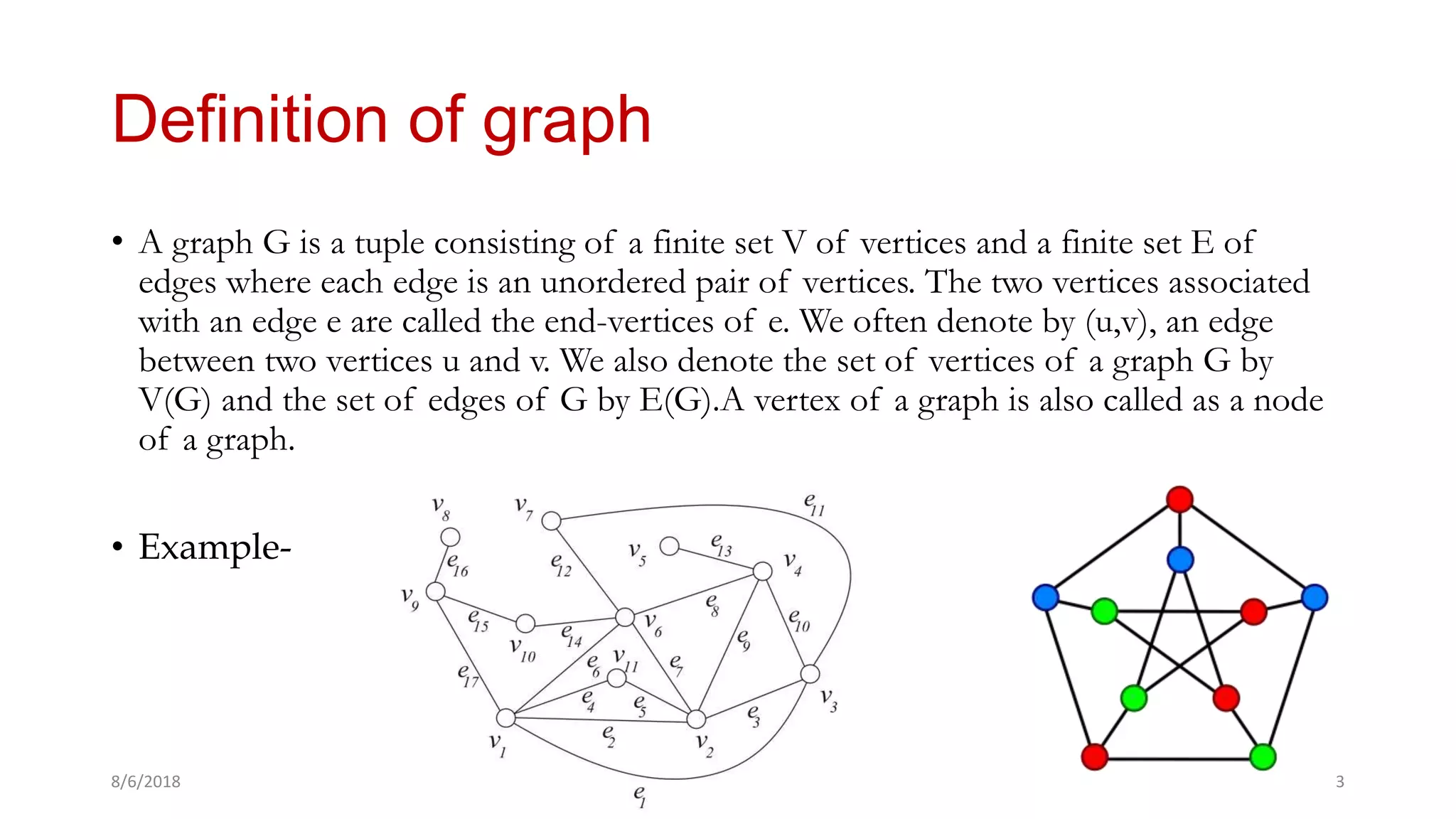
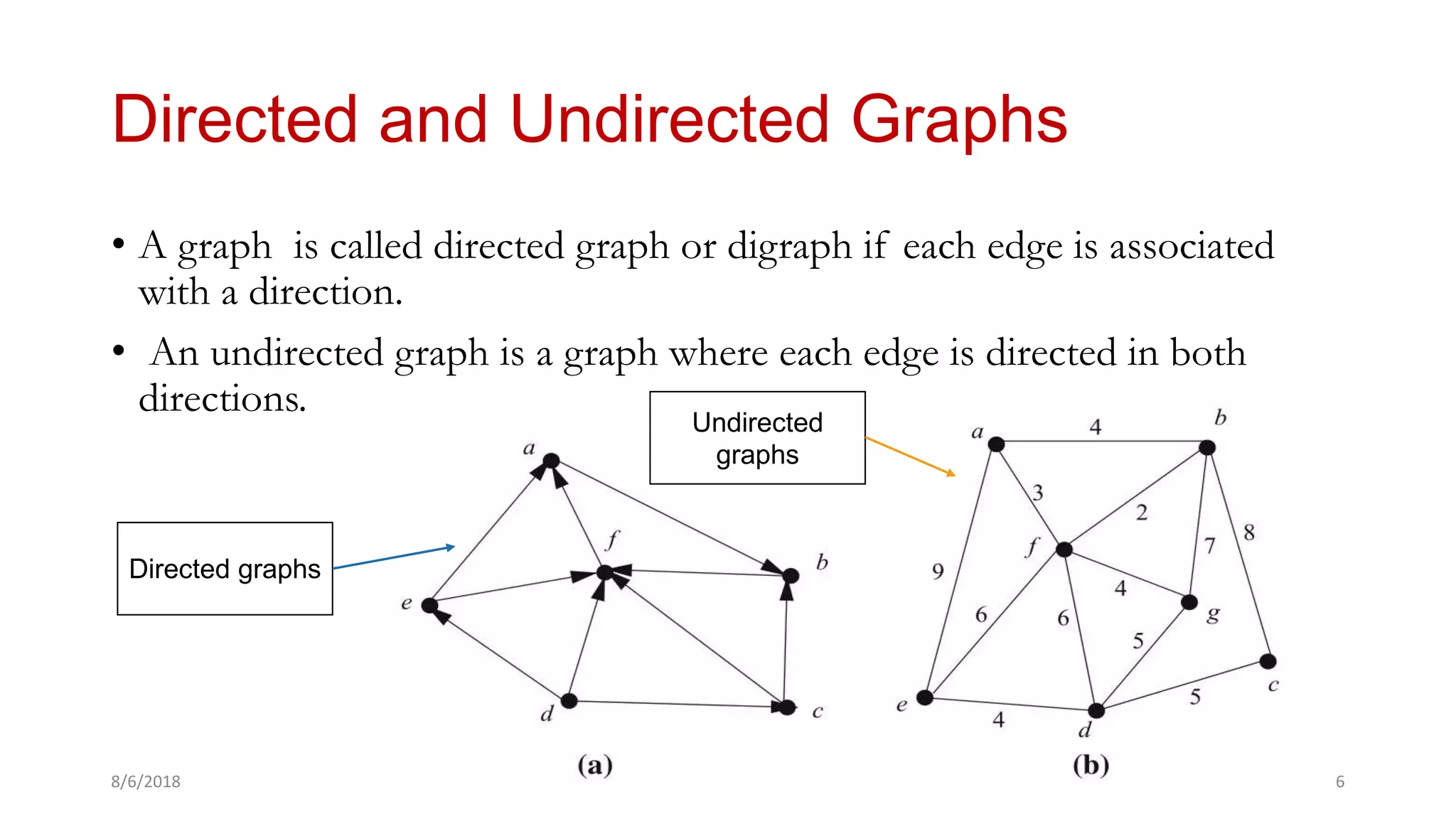
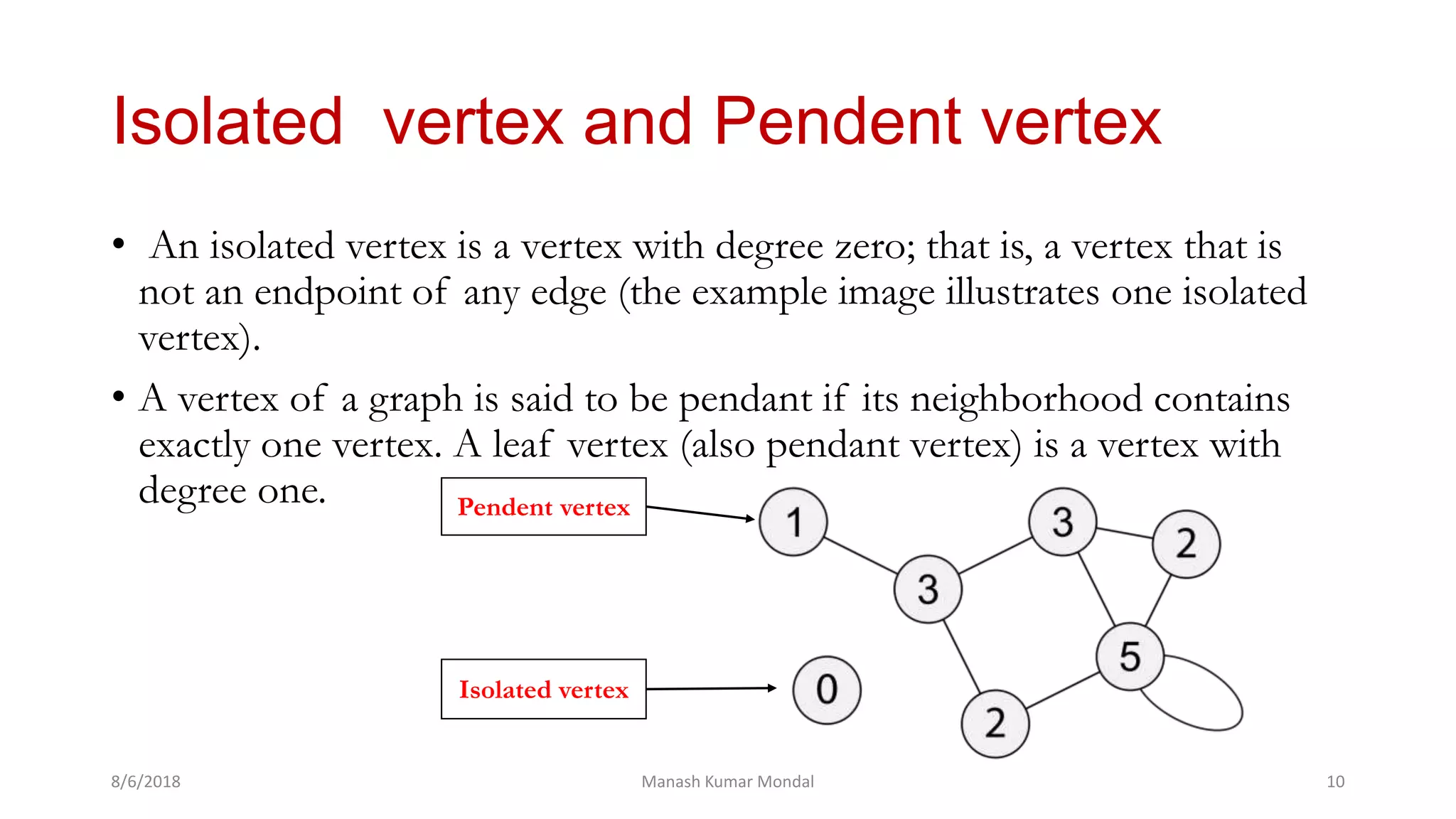
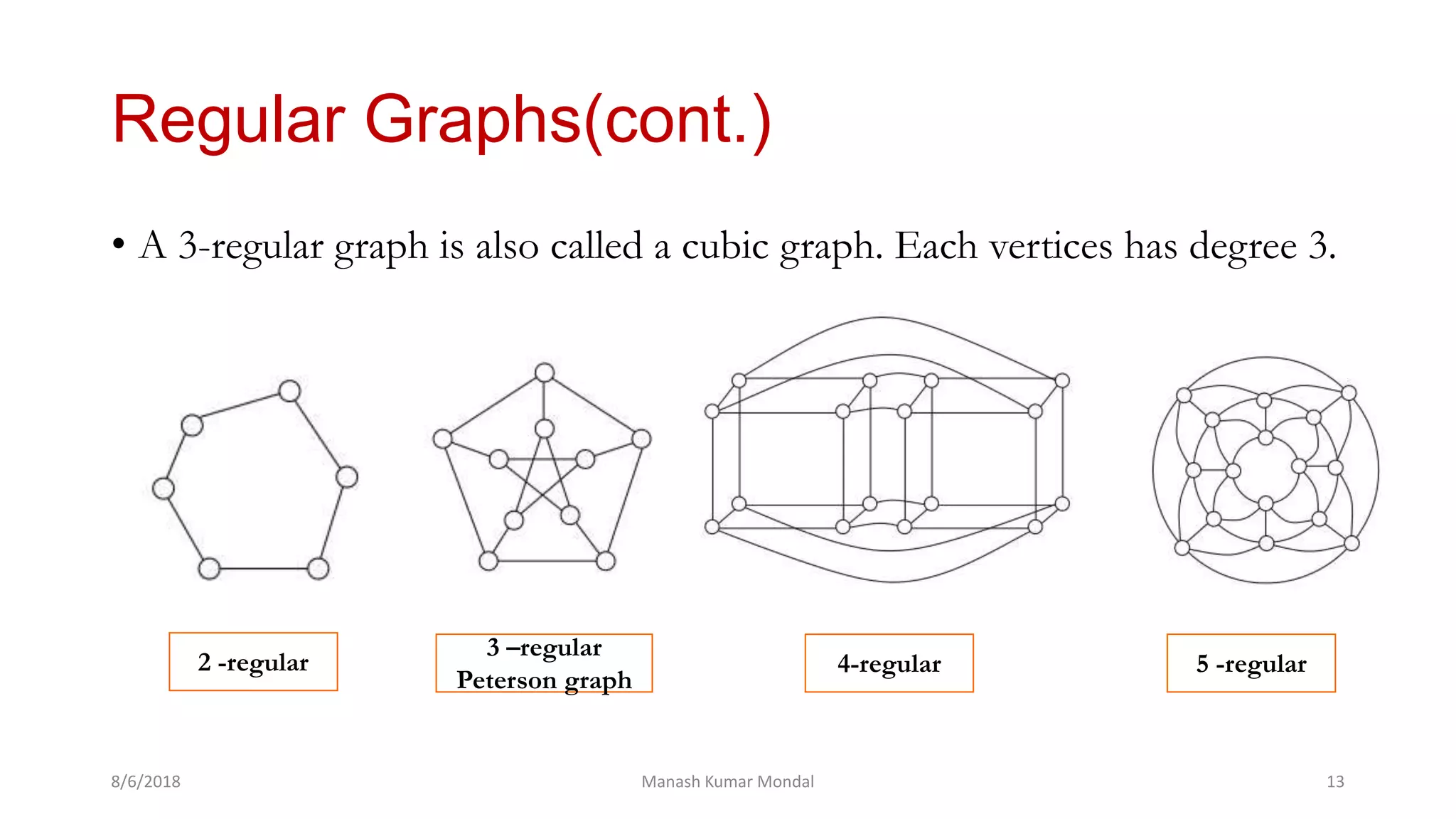
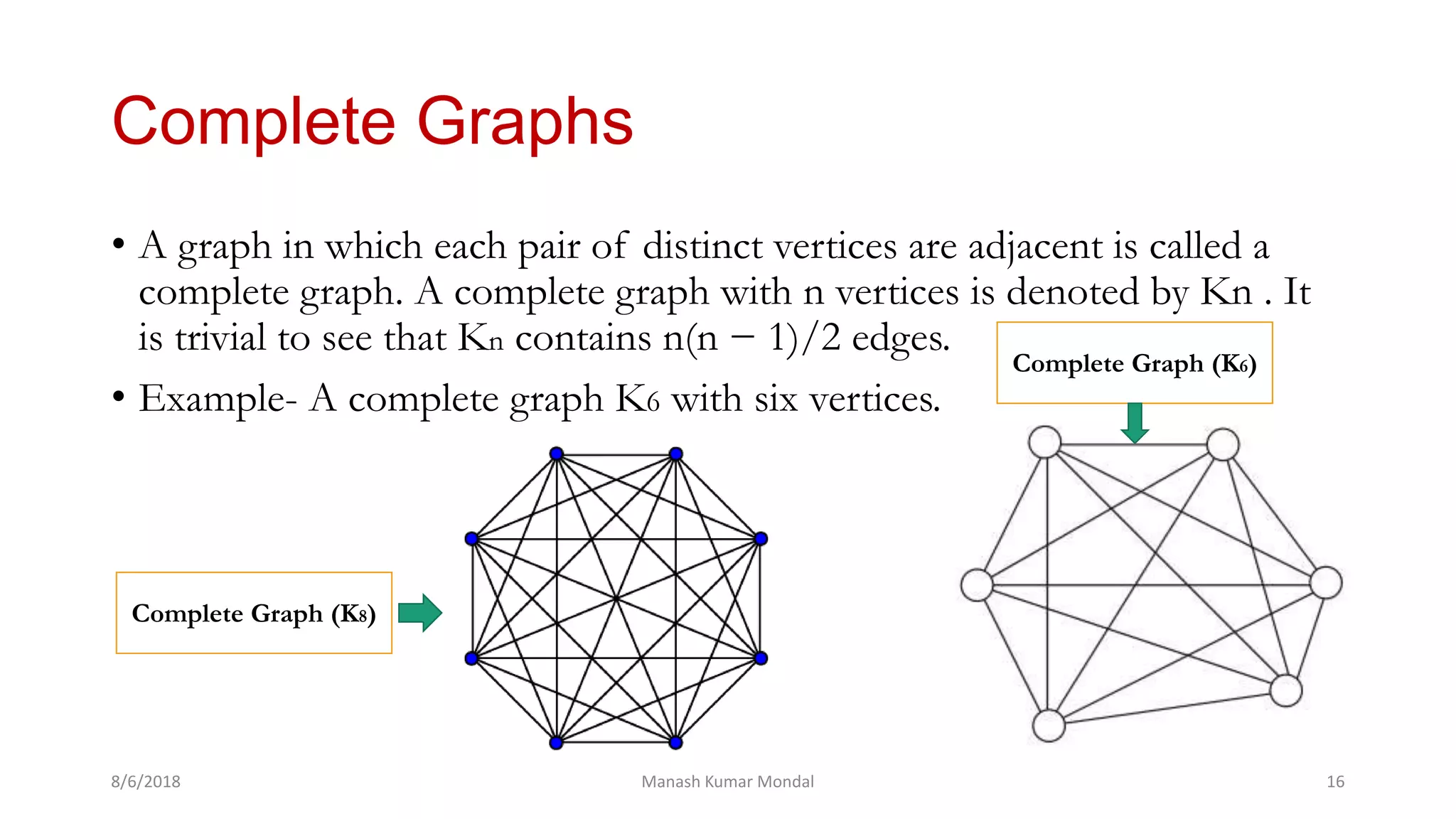
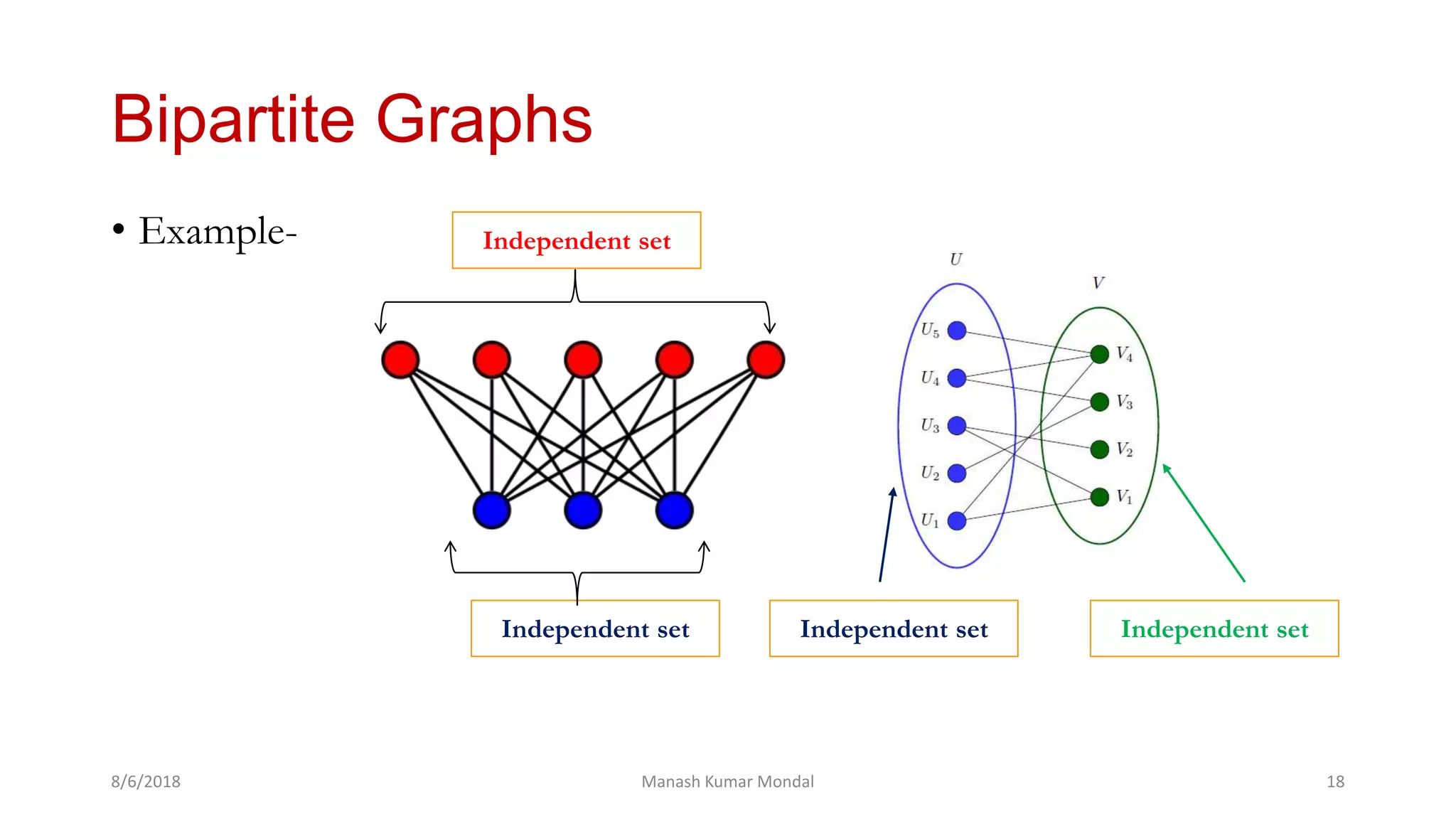
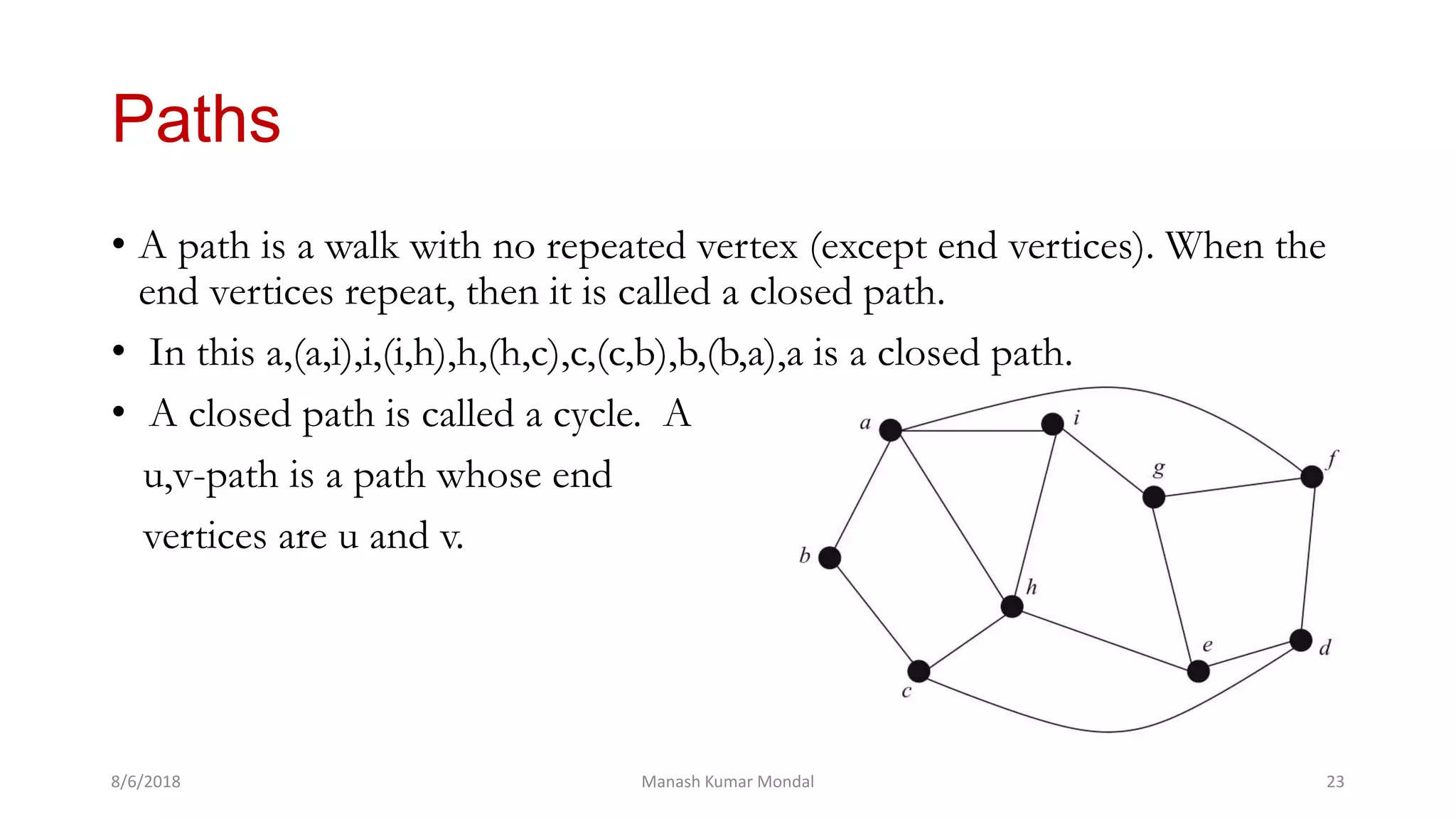
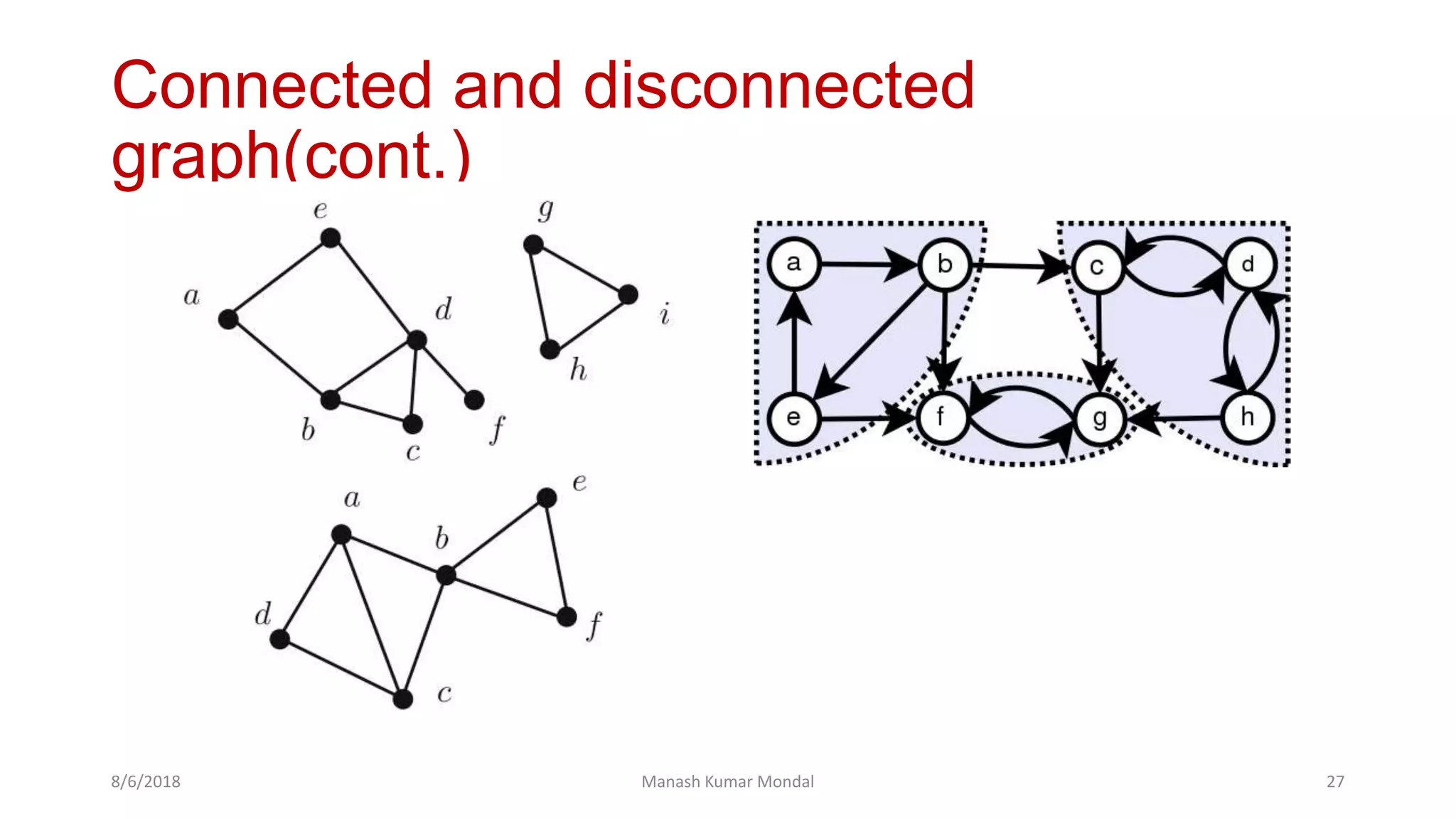
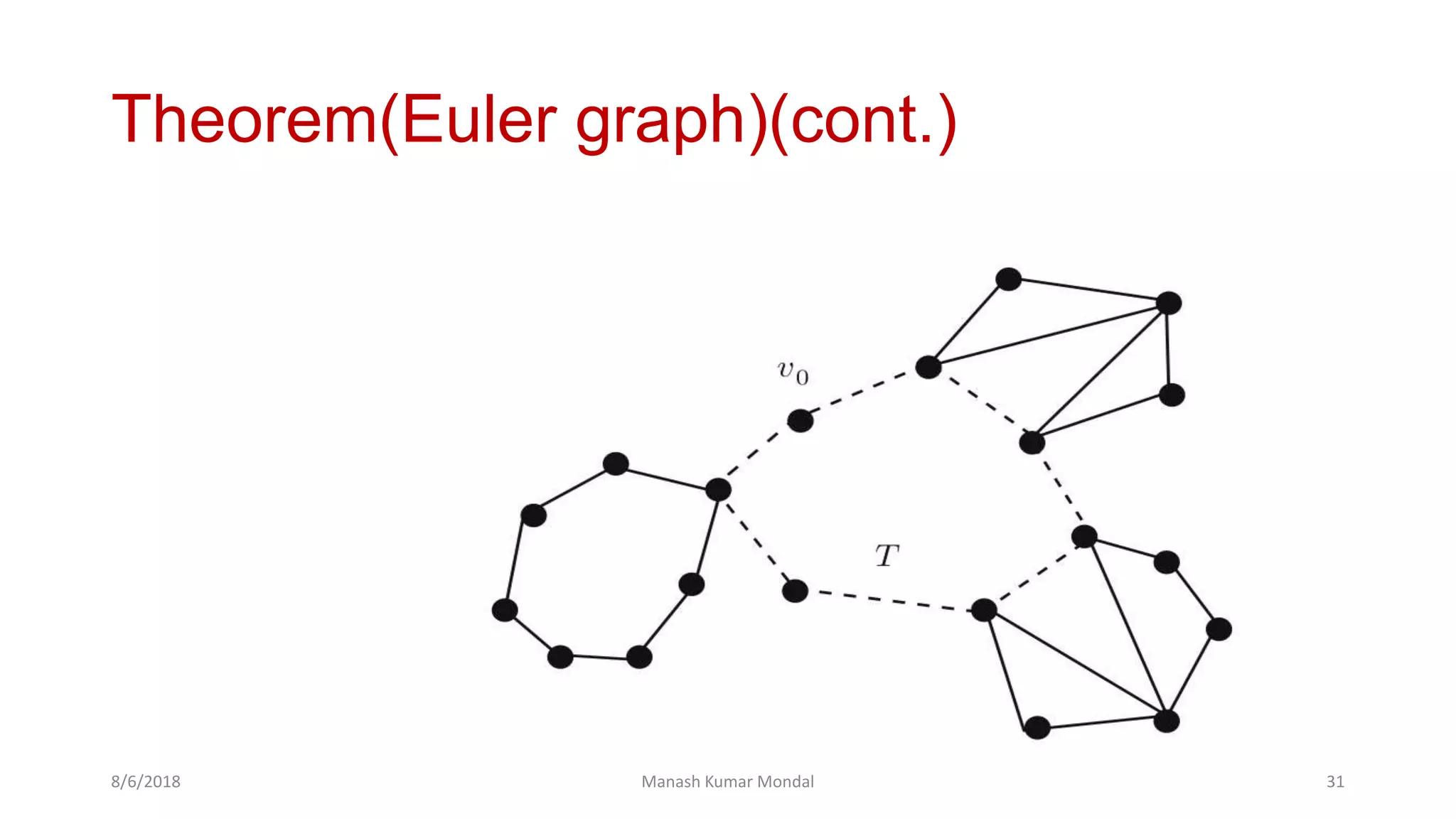
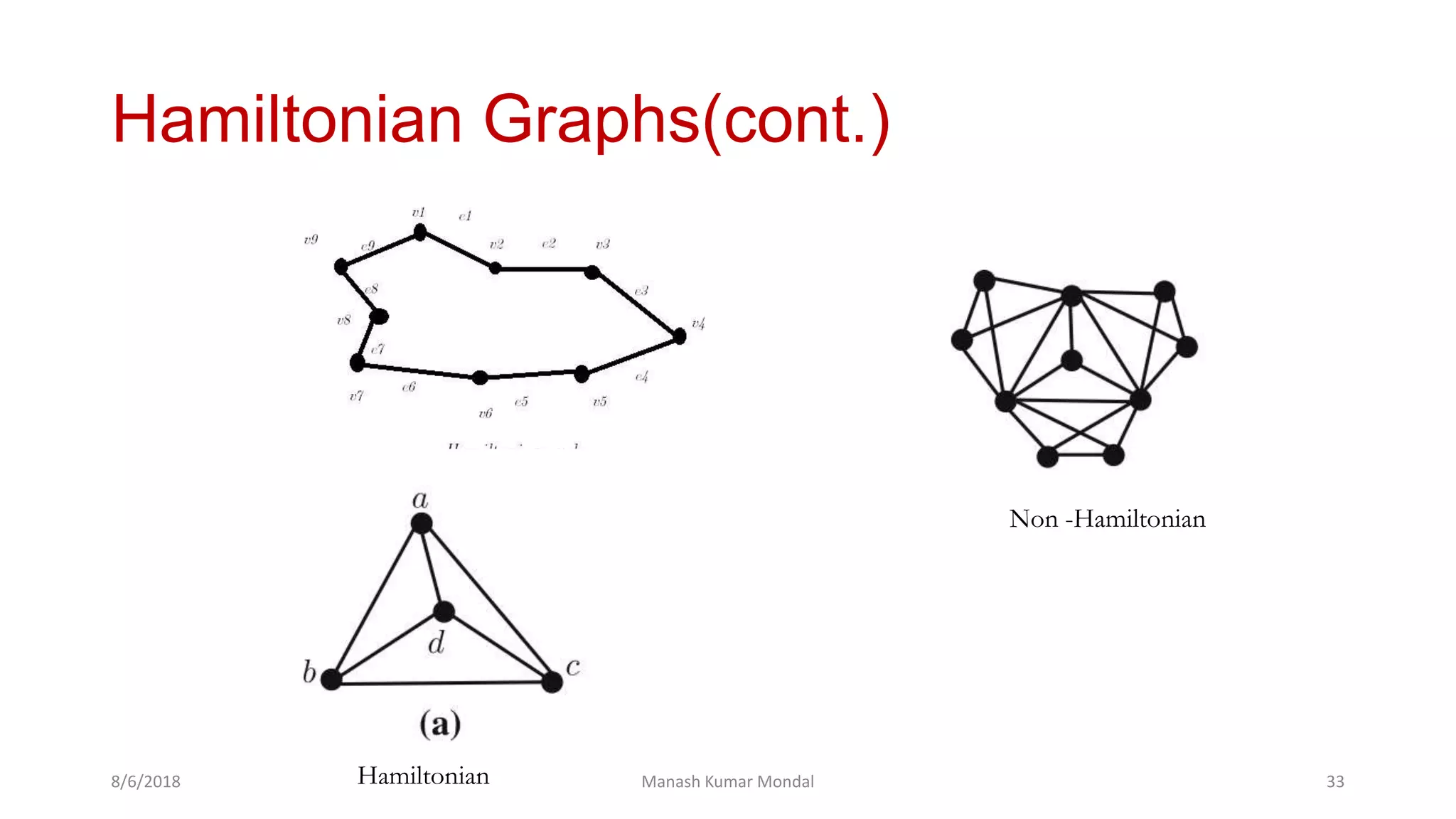
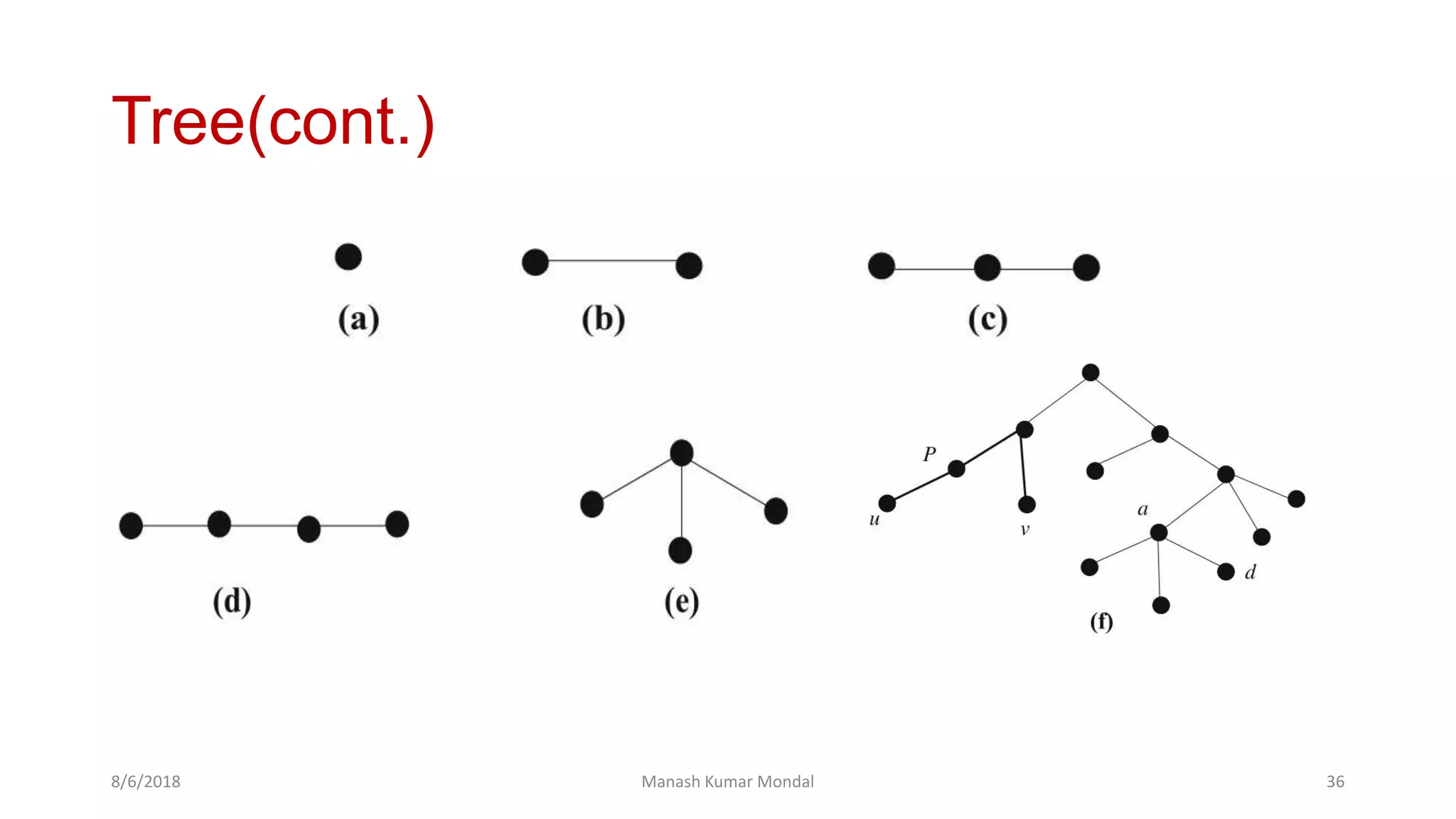
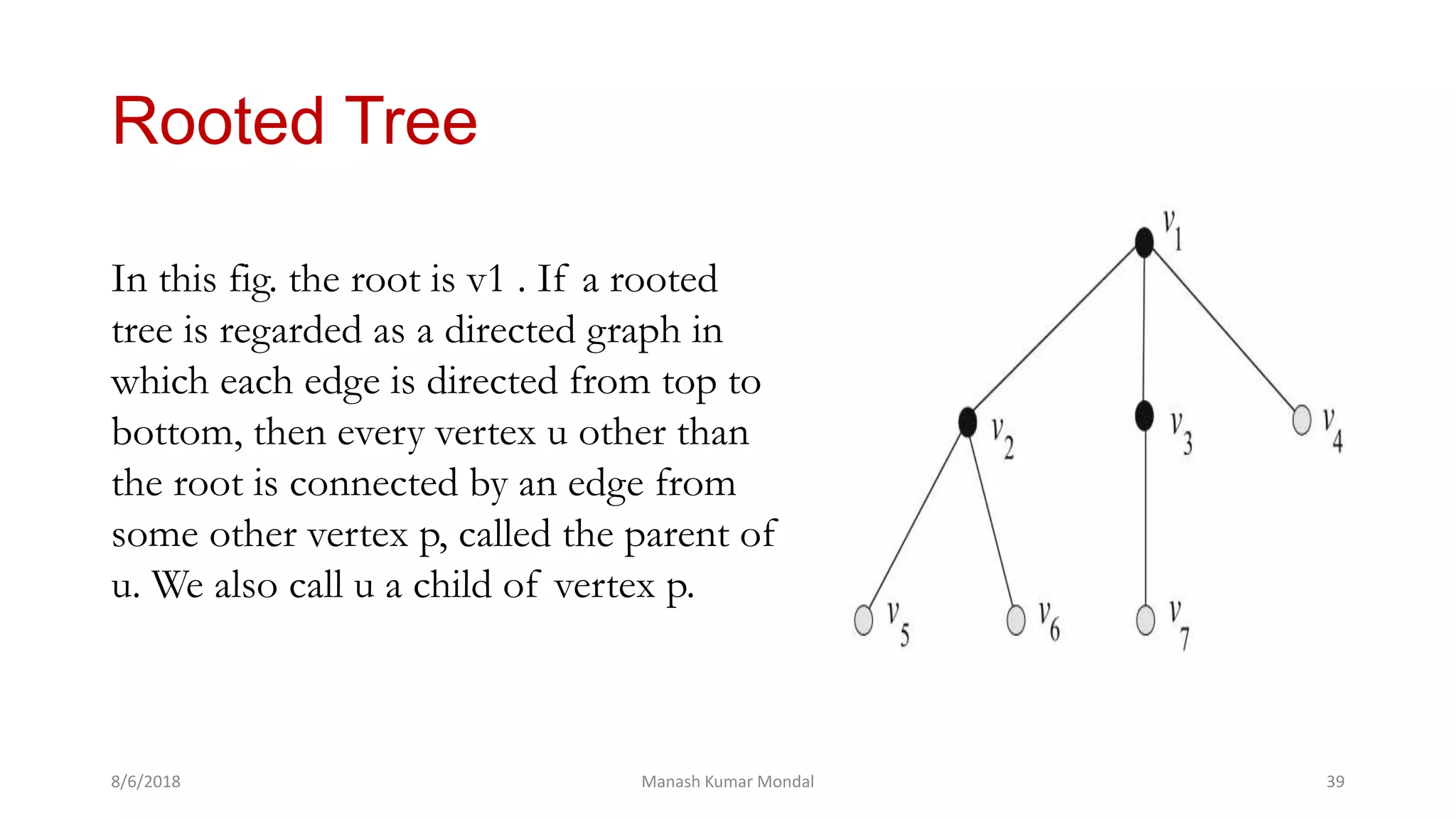
The document provides a comprehensive overview of graph theory, outlining key concepts such as definitions, types of graphs (finite, infinite, directed, undirected), and essential components like vertices, edges, paths, circuits, and connectedness. It delves into specific graph types including eulerian and hamiltonian graphs, as well as tree structures, while detailing properties like vertex degrees and subgraphs. The document serves as a foundational text for understanding the principles and applications of graph theory.