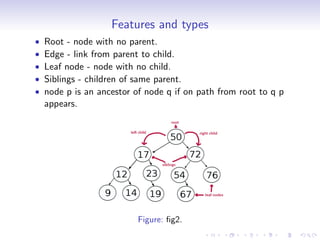
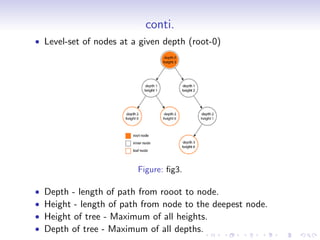
A tree is a hierarchical data structure where each node can have many children. It consists of a root node, edges that link parents to children, and leaf nodes without children. A binary tree restricts each node to having at most two children. Binary trees can be full, complete, or strict depending on how nodes are structured. Common operations on binary trees include inserting, deleting, searching, and traversing nodes. Binary trees have applications in compilers, data compression, search trees, and priority queues.

1. What is a Tree
Figure: fig1.
• A data structure similar to linked list.
• Each node points many other.
• Hierarchical nature in graphical form.

2. Features and types
• Root - node with no parent.
• Edge - link from parent to child.
• Leaf node - node with no child.
• Siblings - children of same parent.
• node p is an ancestor of node q if on path from root to q p
appears.
Figure: fig2.

3. conti.
• Level-set of nodes at a given depth (root-0)
Figure: fig3.
• Depth - length of path from rooot to node.
• Height - length of path from node to the deepest node.
• Height of tree - Maximum of all heights.
• Depth of tree - Maximum of all depths.

4. conti.
Conti.
• Size - Number of descendants including itself.
• Skew Trees - Every node in tree has one child.
a. Left Skew tree - only left child.
b. Right Skew tree - only right child.
Figure: fig4.

5. About Binary Trees
• Binary Tree
Binary tree -ro,one or two children. Essentially root and two
disjoint binary trees .
Figure: fig5.

6. Types Of Binary Trees
• Types of Binary Trees
1. Strict Binary Tree - Each node exactly two or no children.
Figure: fig6.
1. Full Binary Tree - Each node 2 children, all leaf nodes same
level.
Figure: fig6.2.
1. Complete Binary Tree - every level, except possibly the last, is
completely filled, and all nodes are as far left as possible..

7. Properties of Binary Trees
Figure: fig7.1.
Figure: fig7.2.

8. Infering from table
• Conti
We infer:
• No. of nodes = 2h+1 − 1.
• No. of nodes in complete tree are greater than 2h (min.) and
2h+1 − 1(max.)
• No. of leaf nodes in a full binary tree = 2h
• No. of NULL pointers in a complete tree = n + 1(n - total
nodes)

9. Structure of Binary Tree
• Structure of Binary Tree
Figure: fig8.
struct BinaryTreeNode
{
int data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
};

10. Operations on Binary Trees
• Operations on Binary Trees
Basic Operations
* Inserting an element into tree.
* Deleting an element from tree.
* Searching for an element.
* traversing the tree.
Auxiliary Operations
* Finding size of the tree.
* Finding height of tree.
* Finding the level which has maximum sum.
* Finding least common ancestor(LCA).

11. applications
• Applicatons of Binary Tree
• Expression trees - used in compilers.
• Huffman coding trees - used in data compression algorithms.
• Binary Search Trees - support search,insertion and deletion in
O(logn) (average).
• Priority Queues - support search and deletion in logarithmic
time(worst case).

12. End