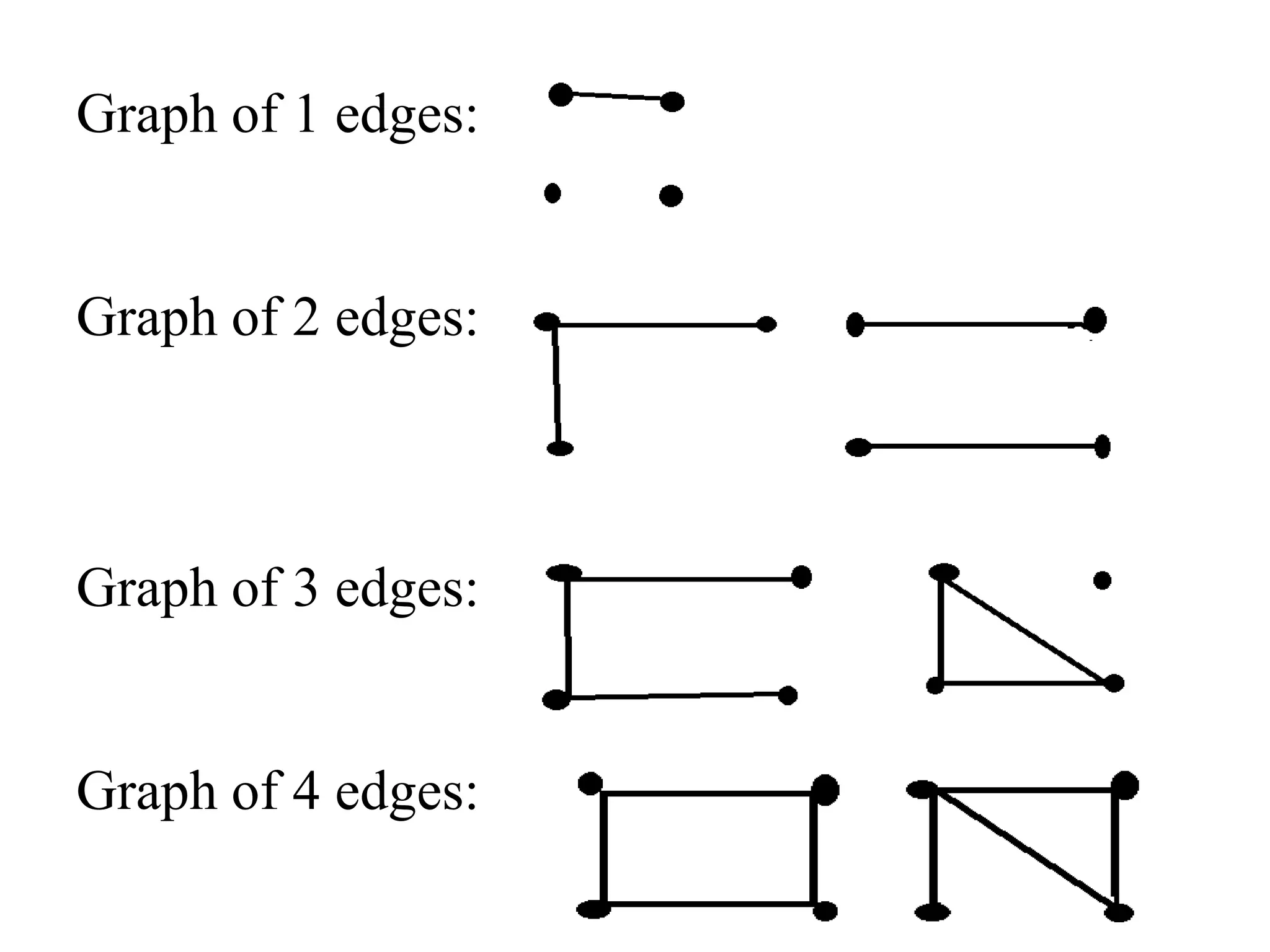
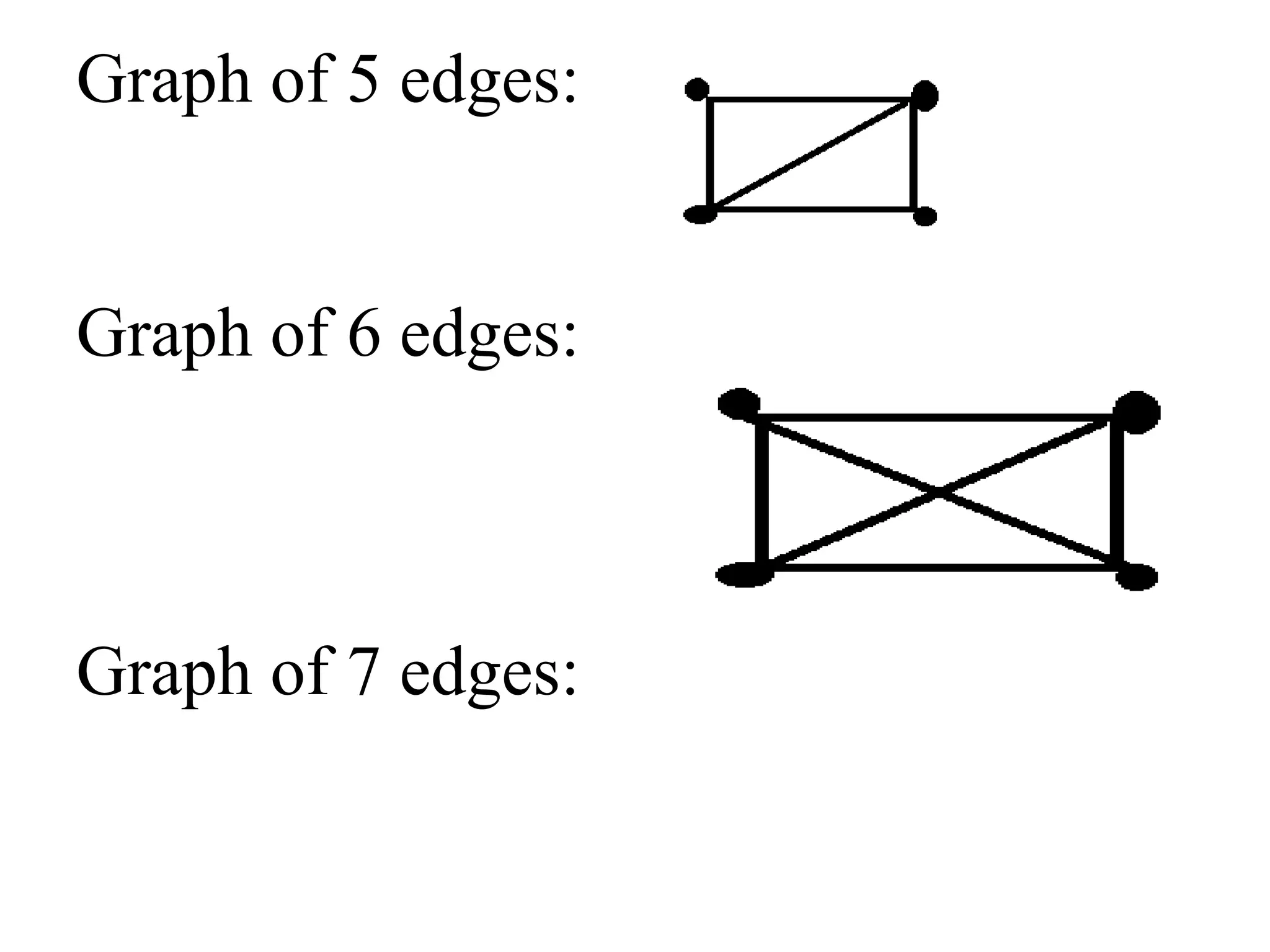
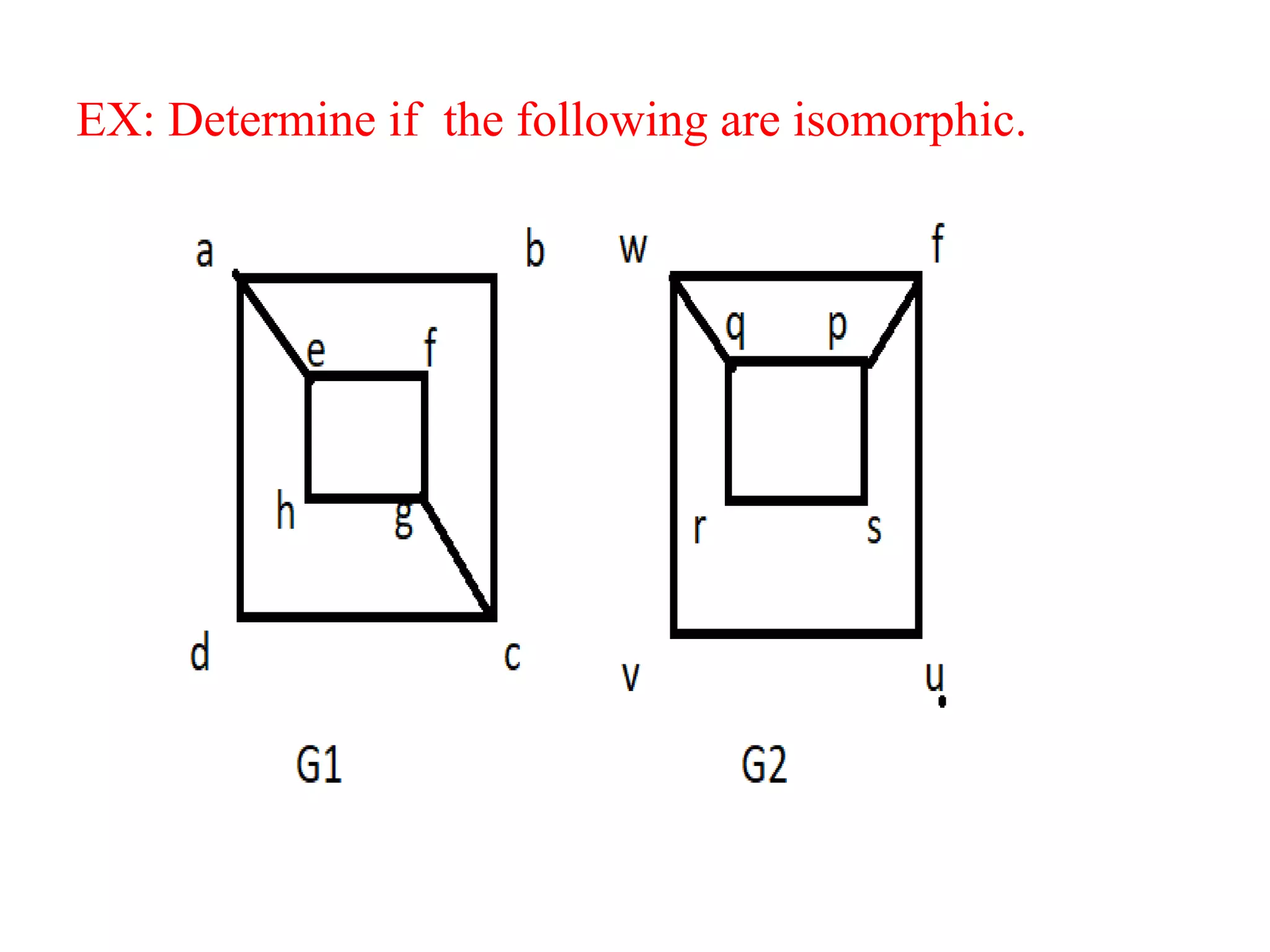
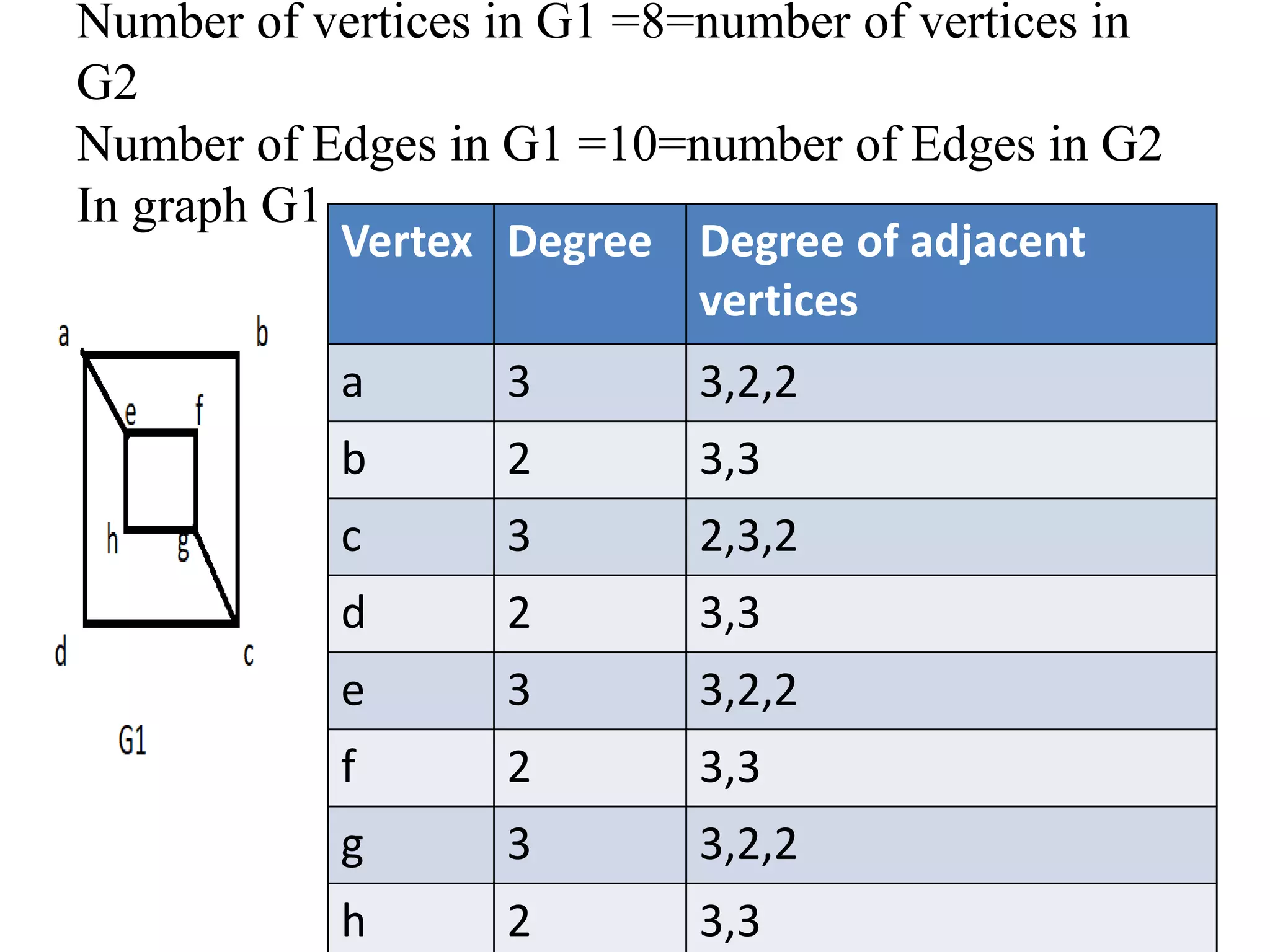
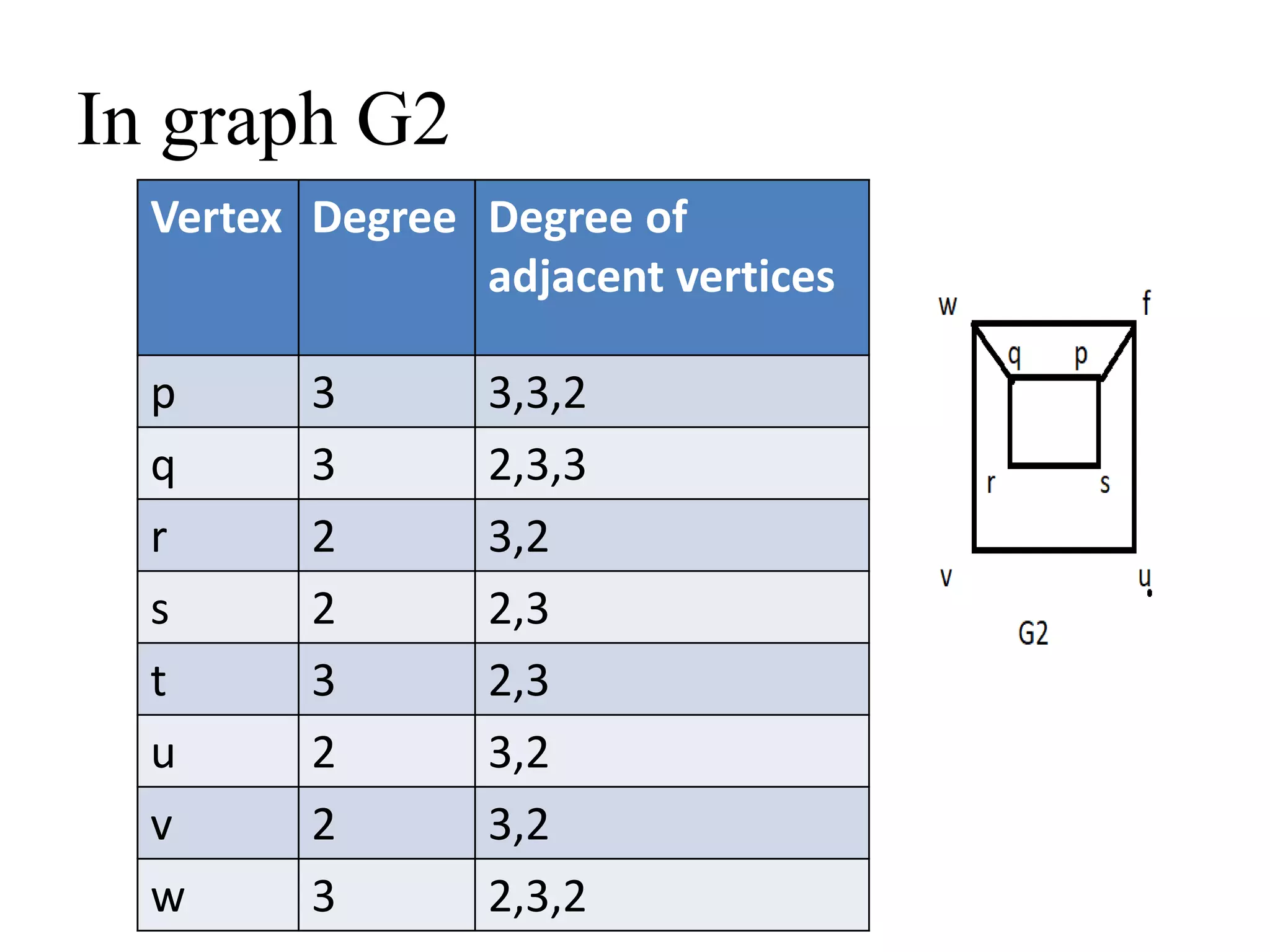
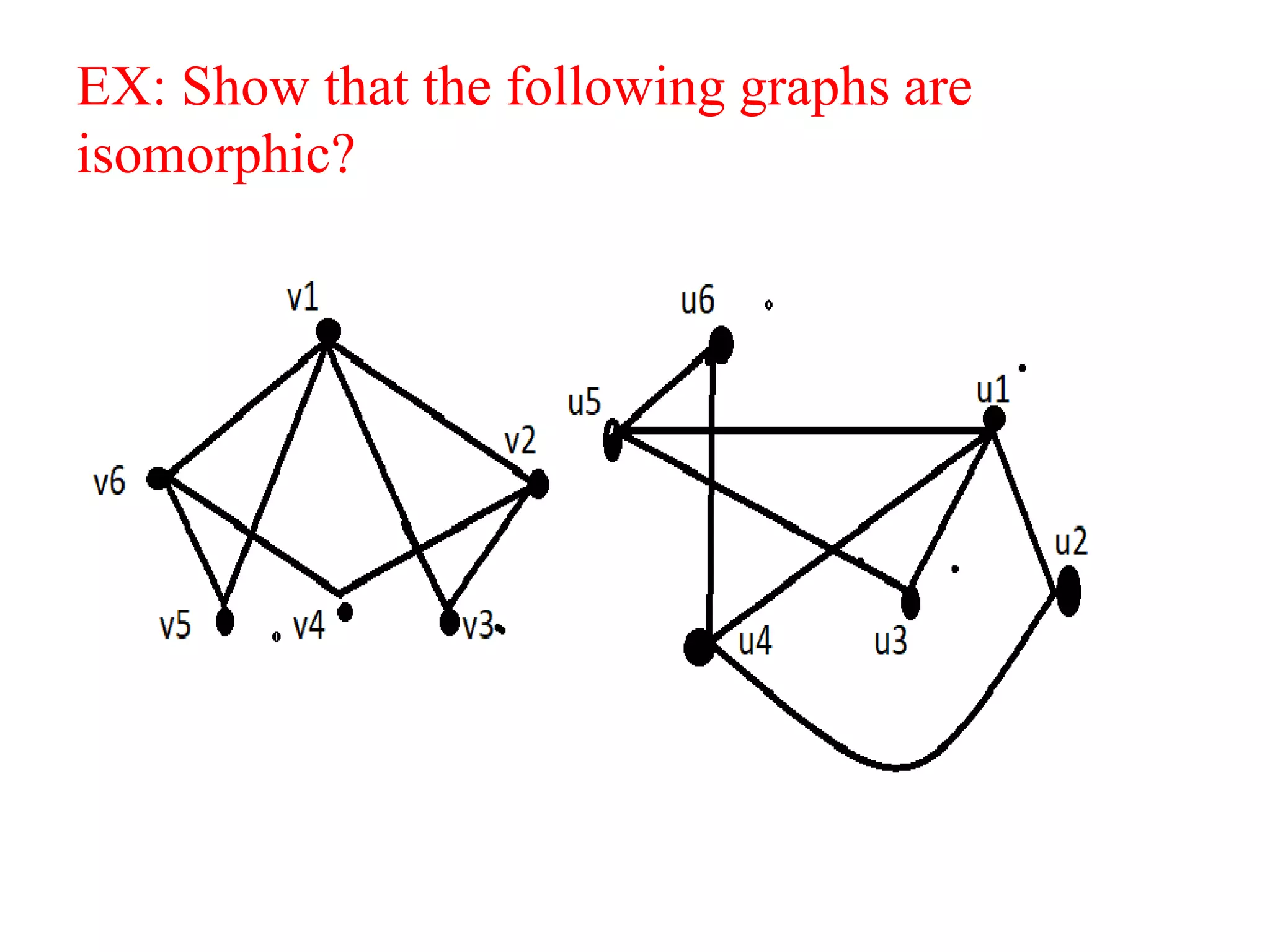
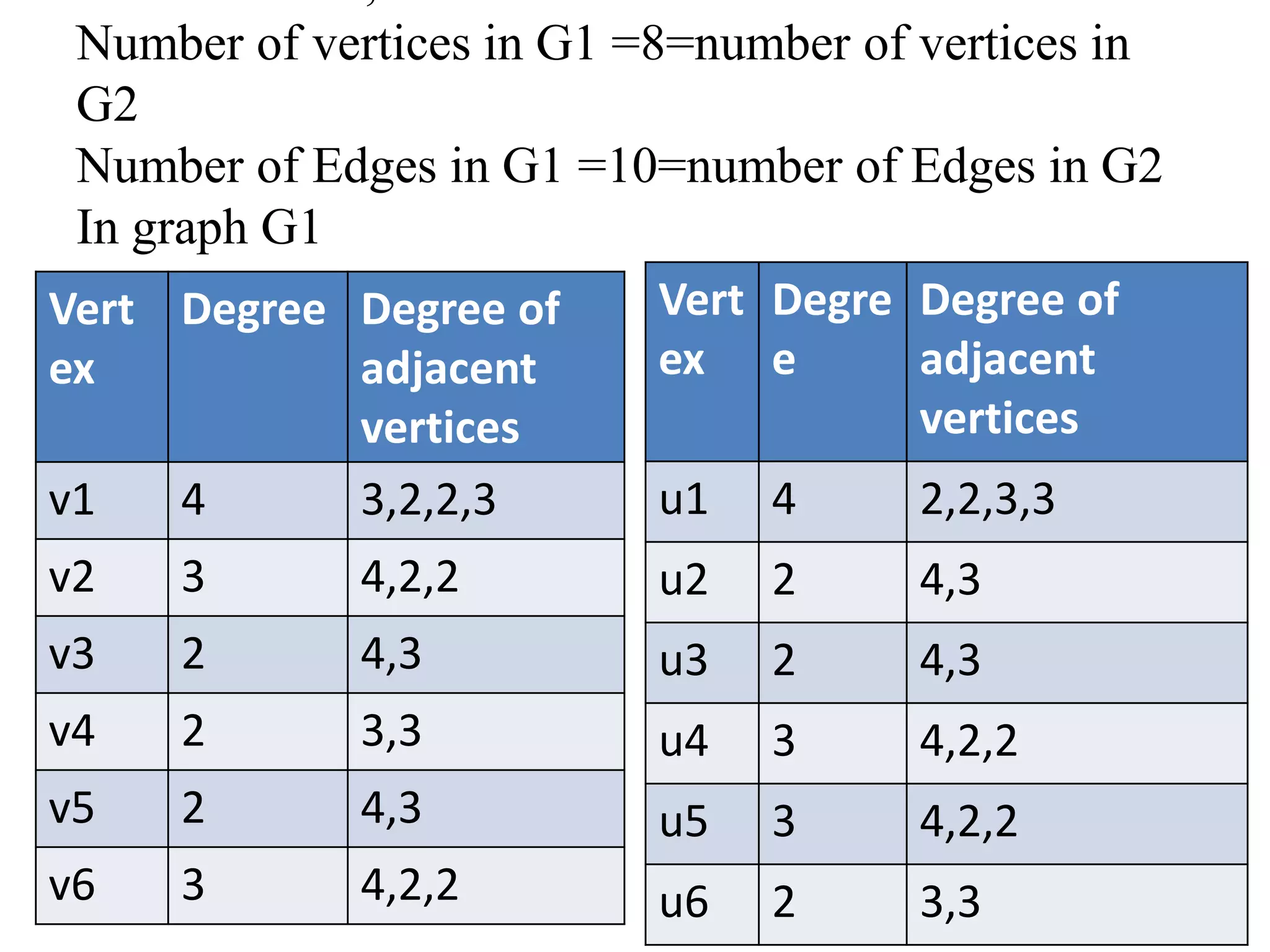
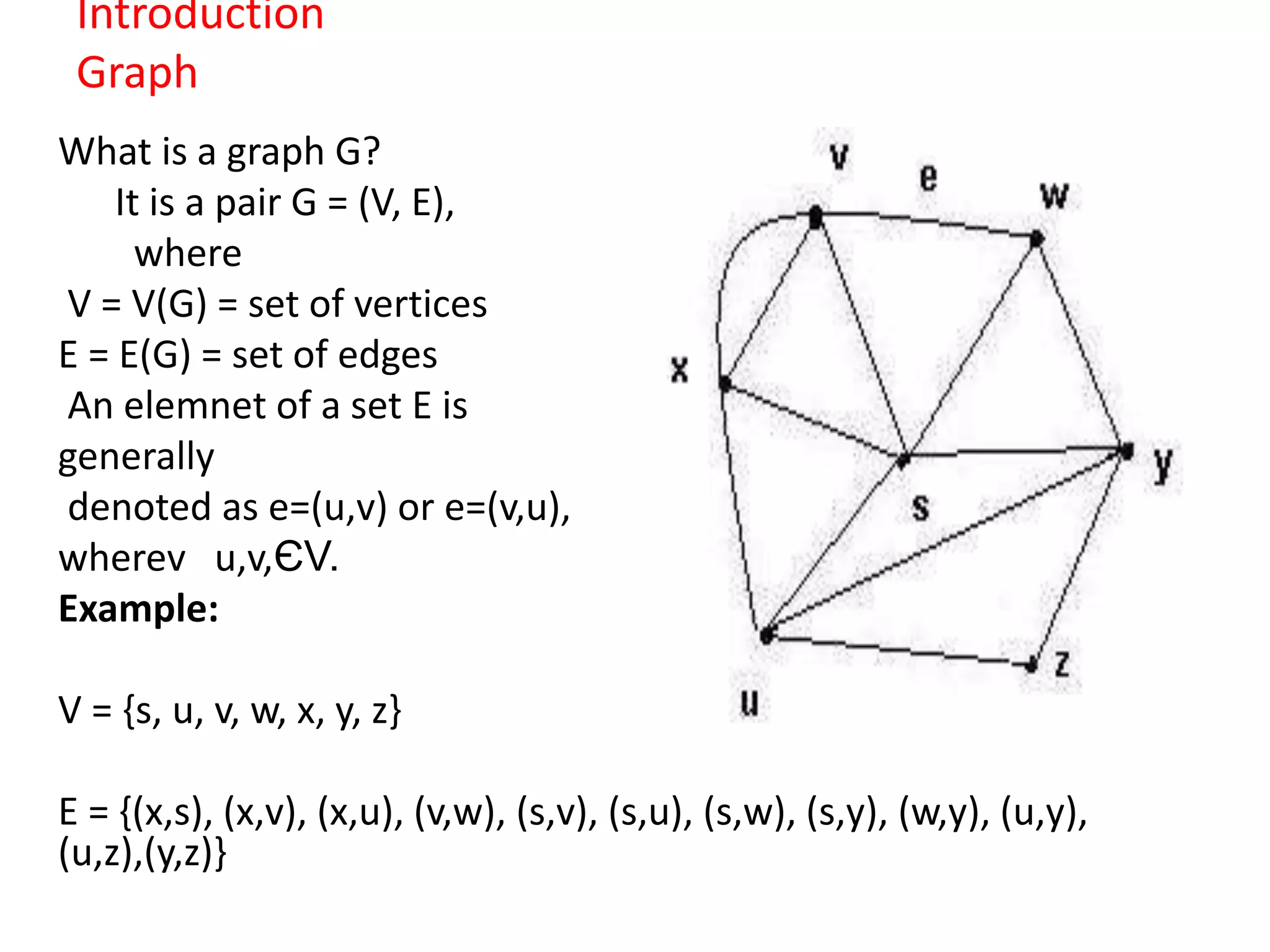
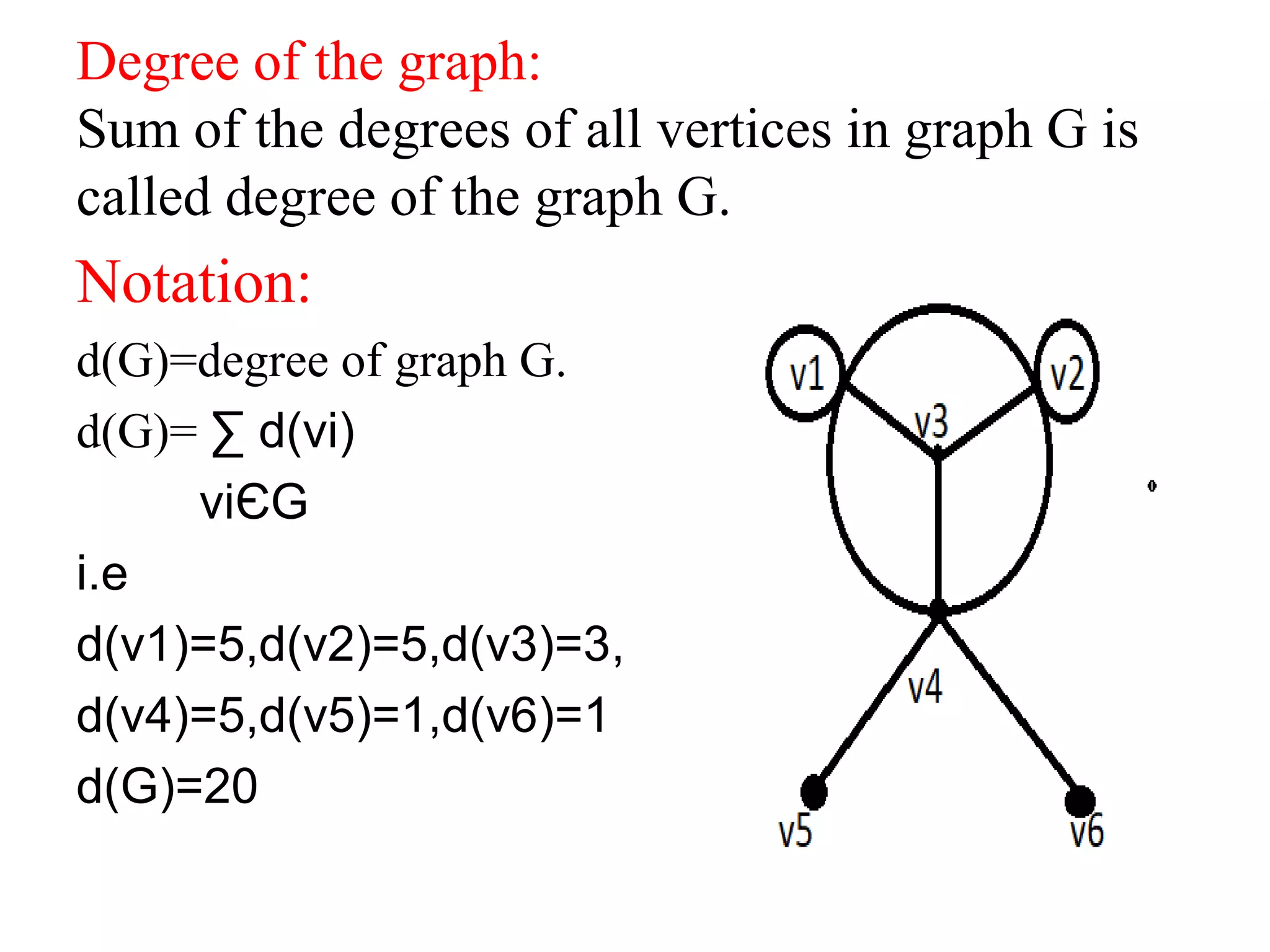
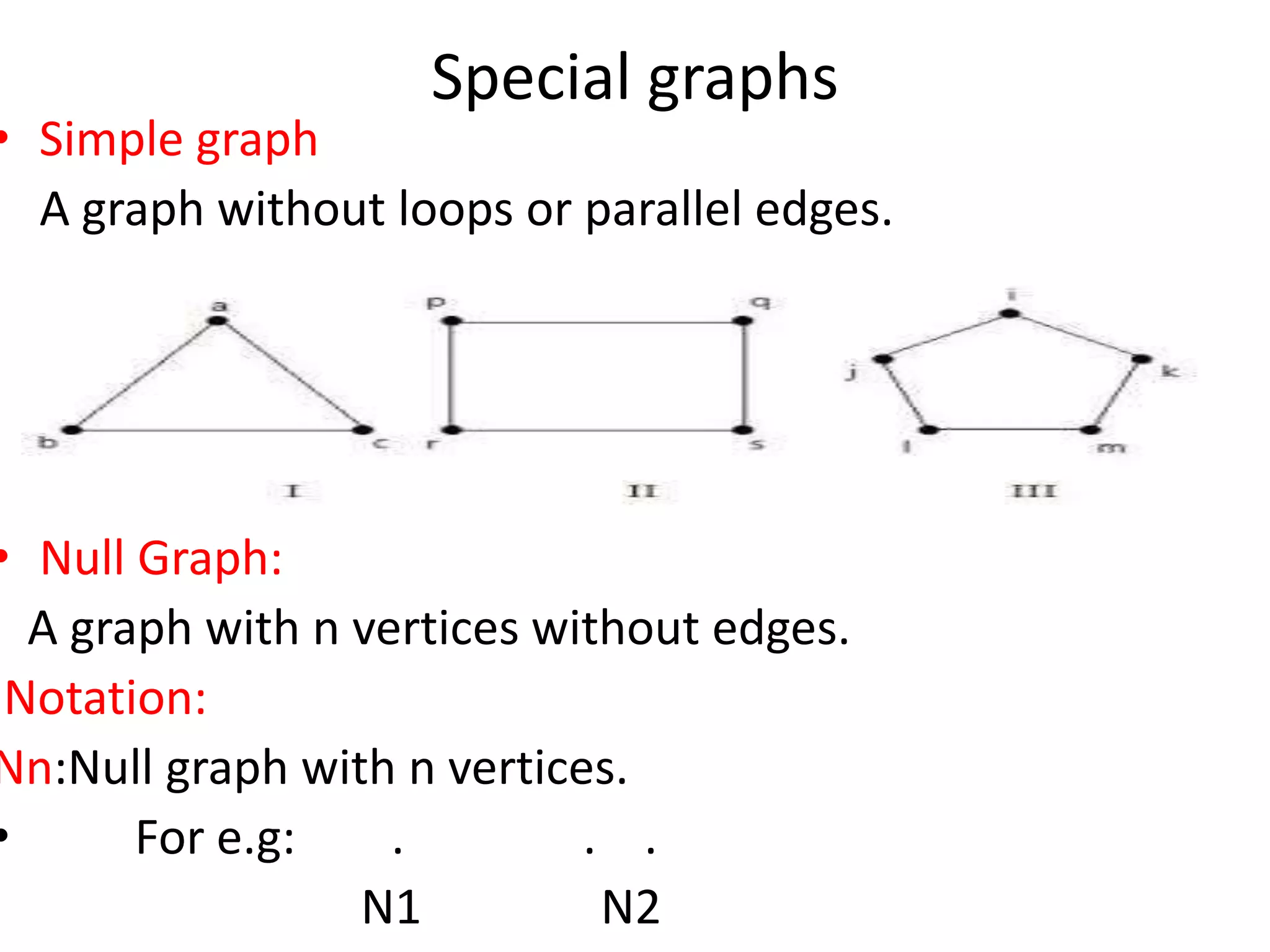
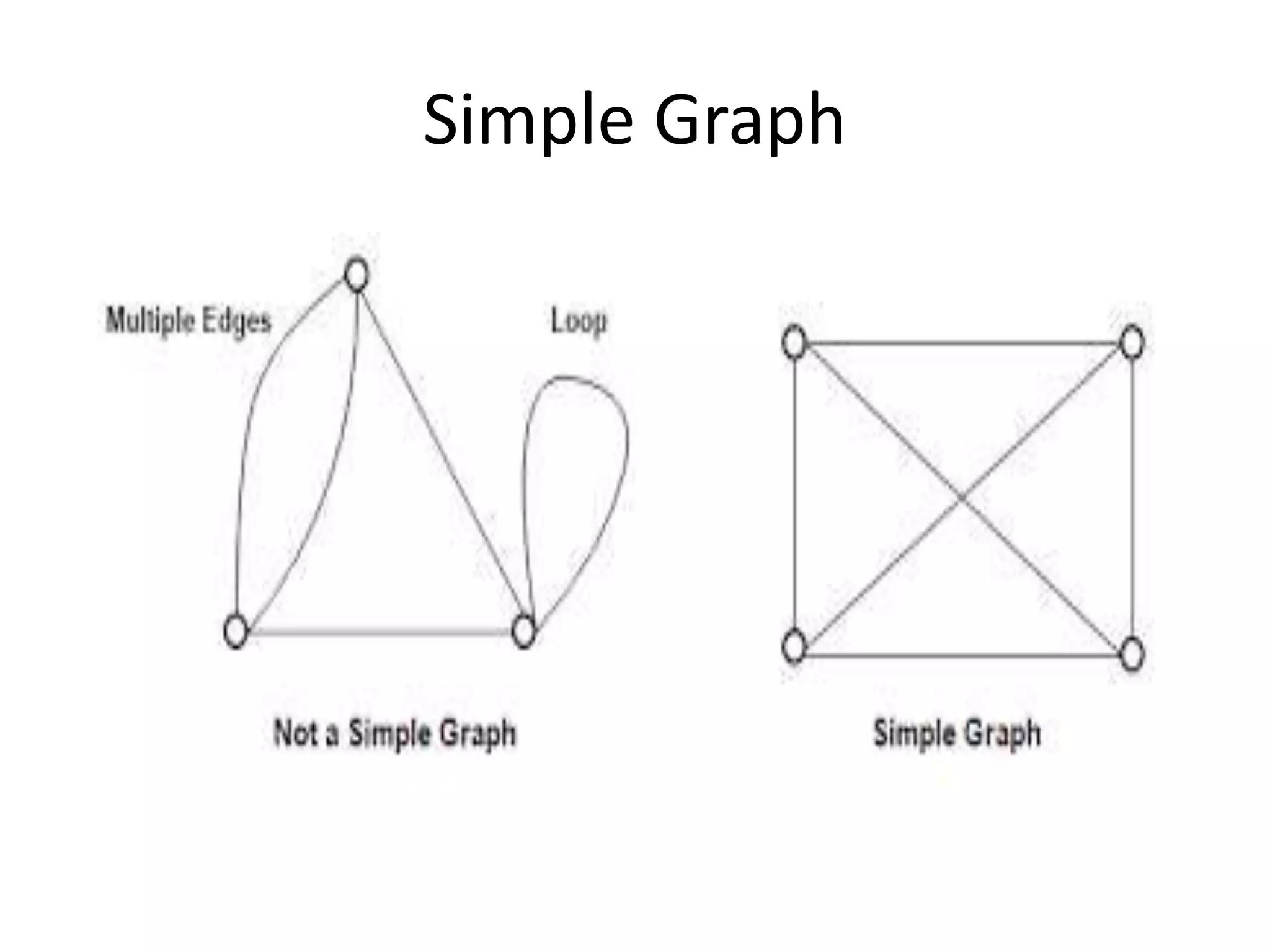
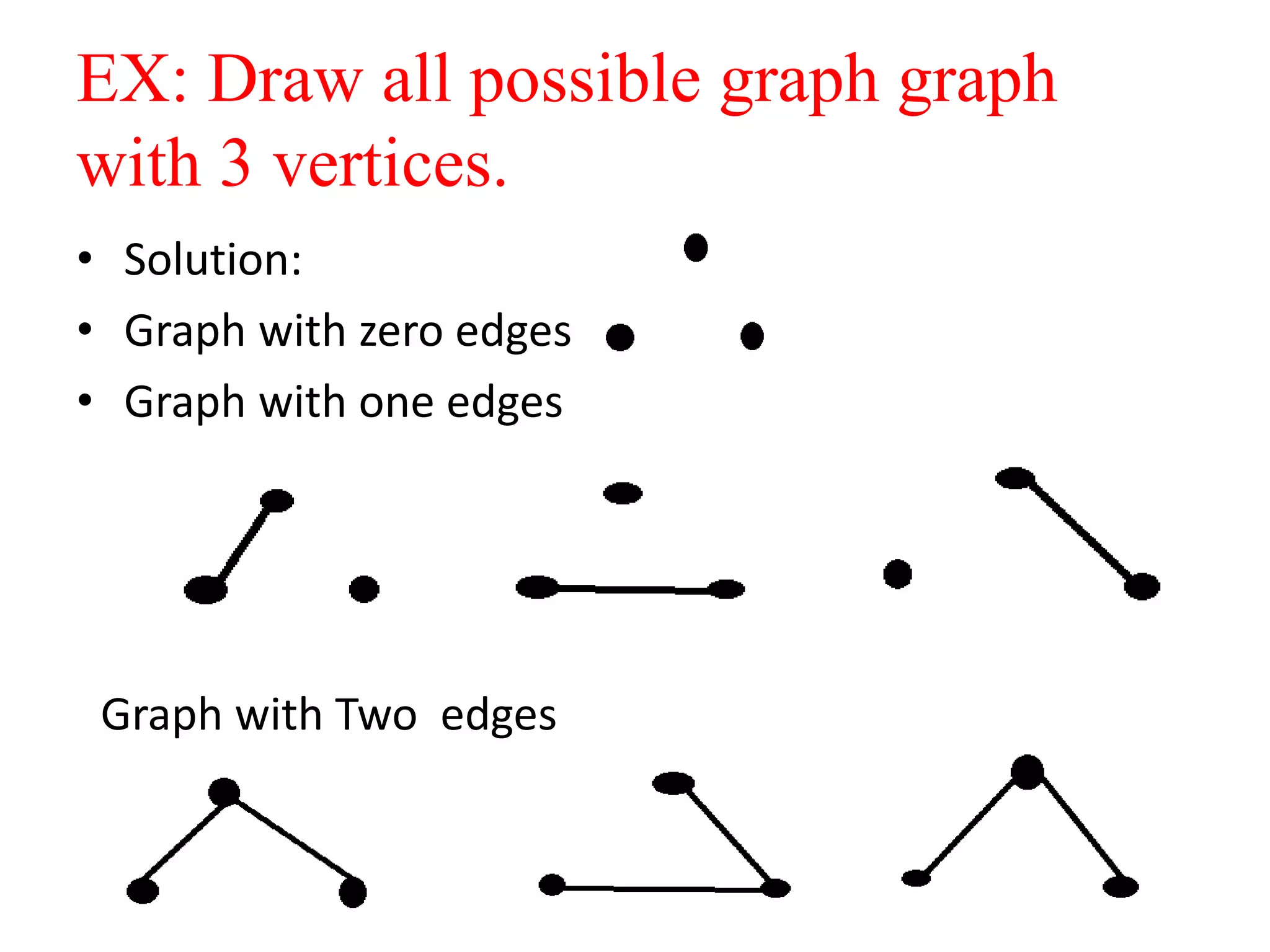
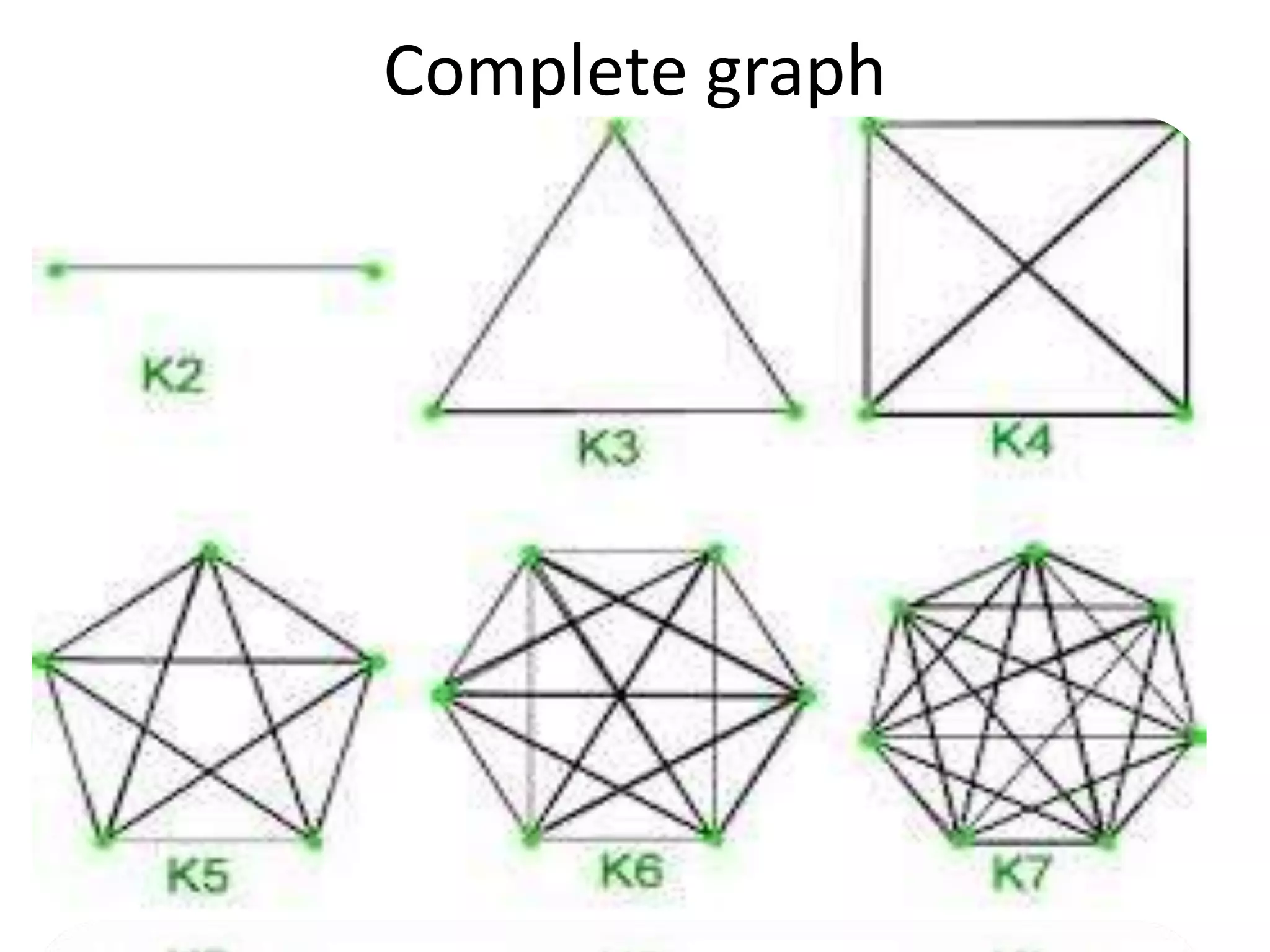
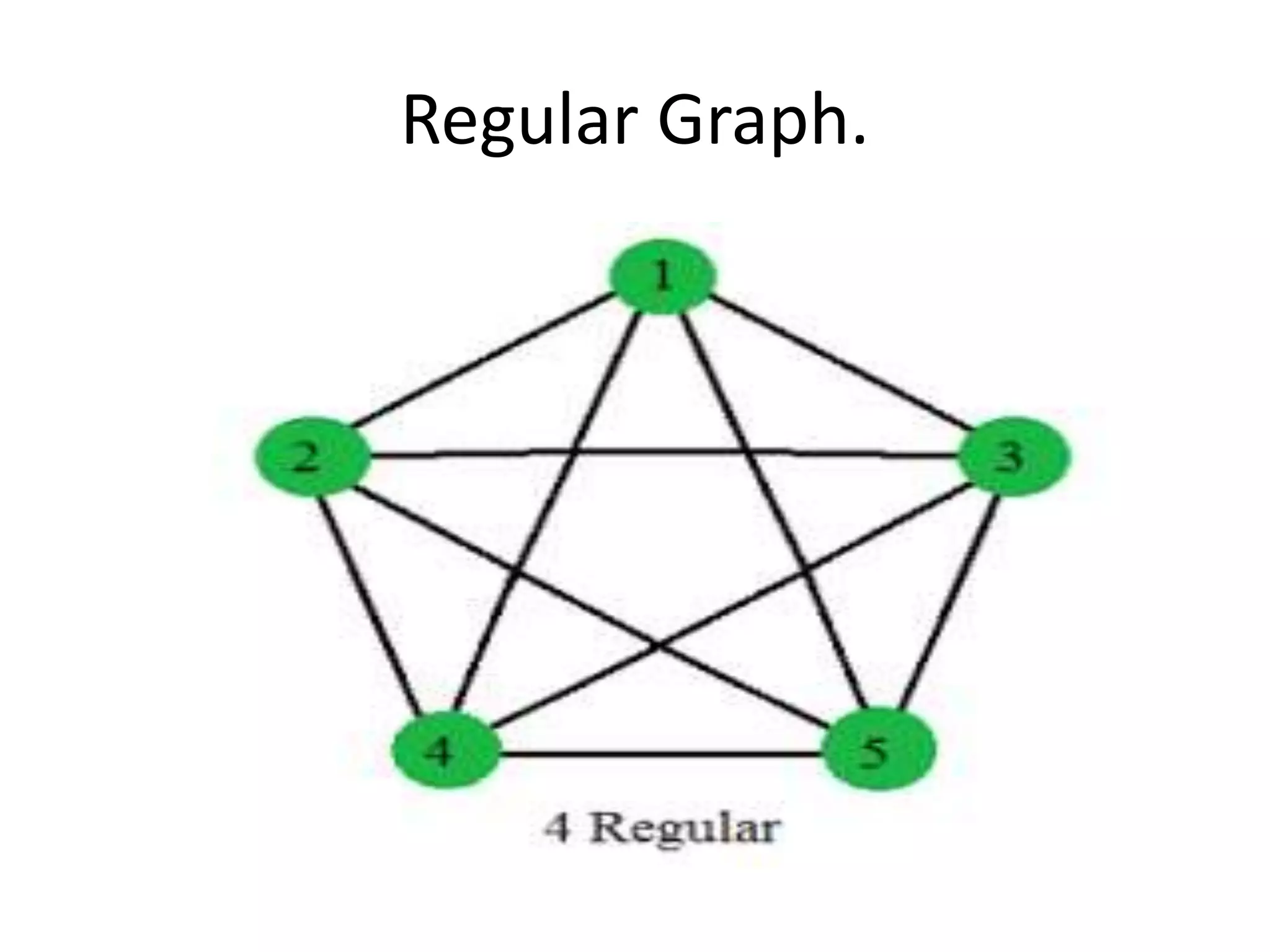
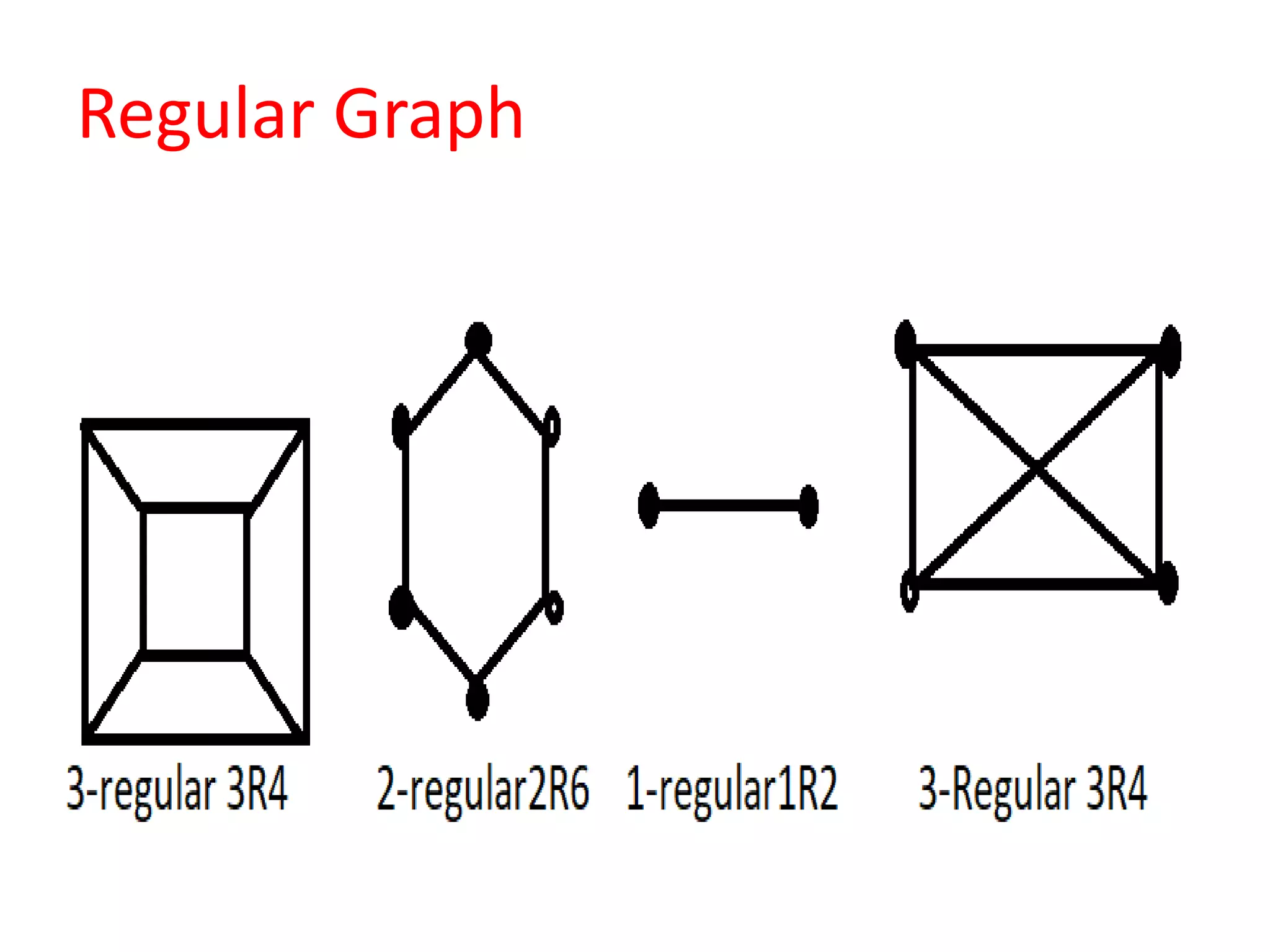
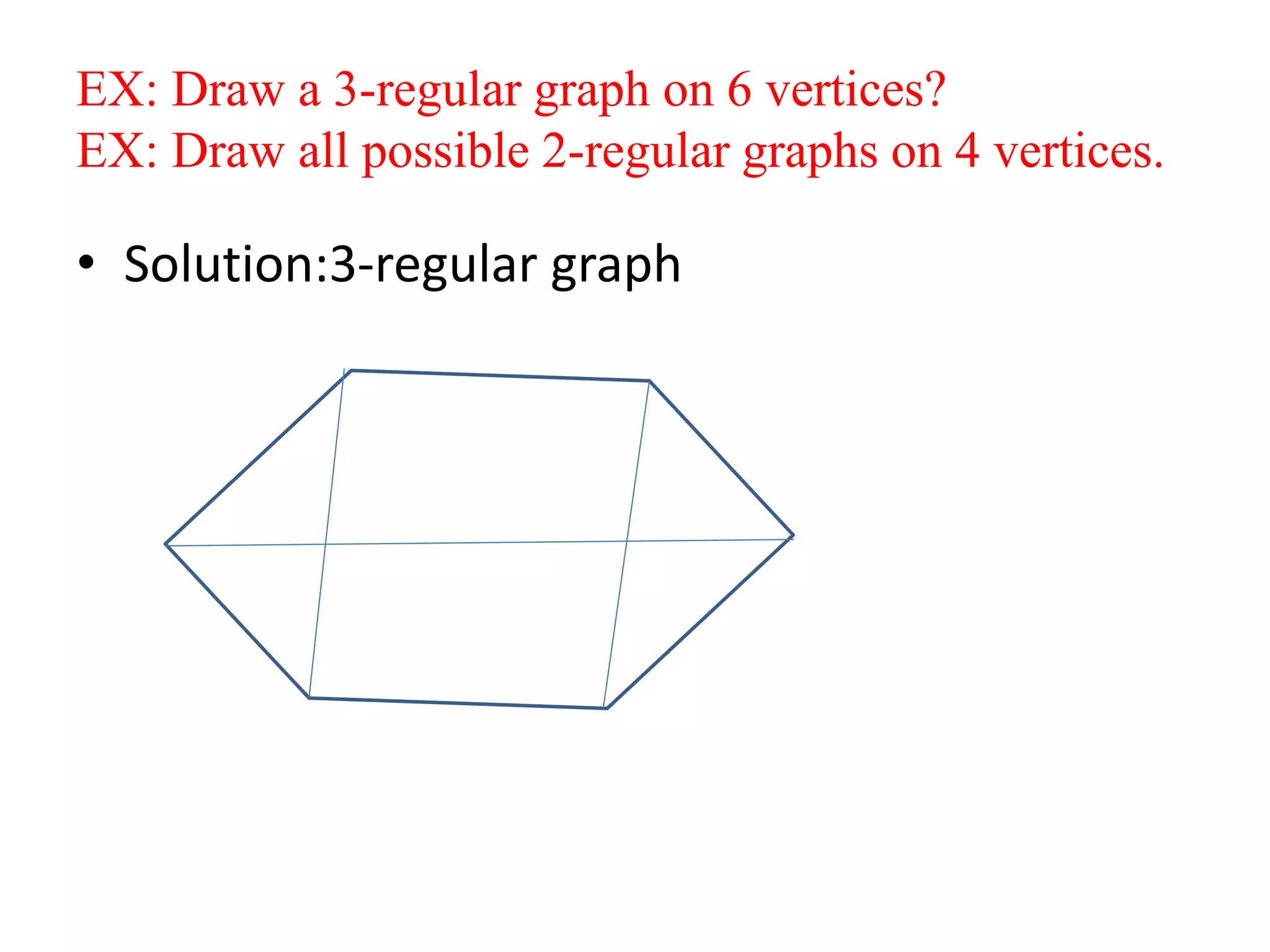
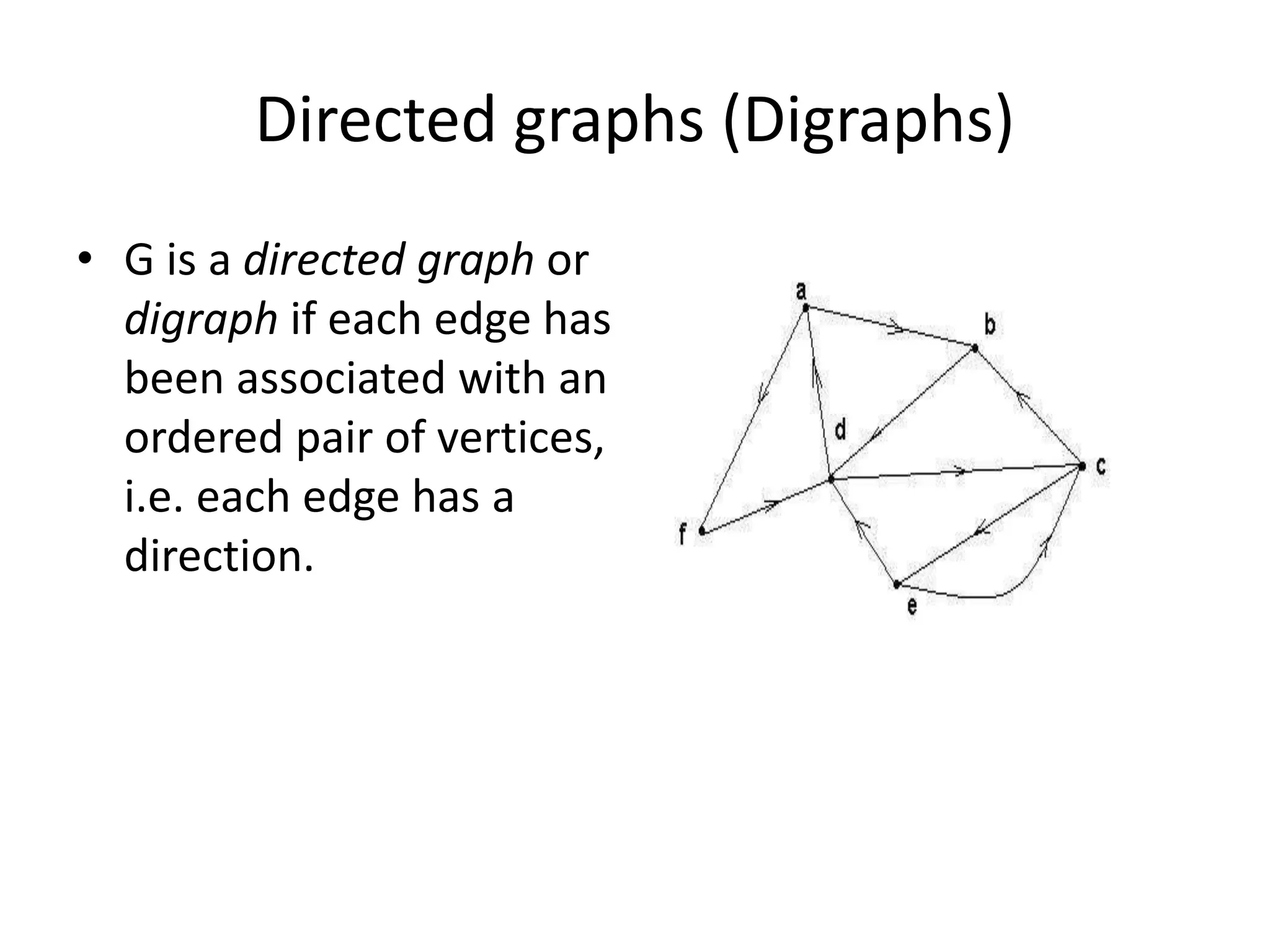
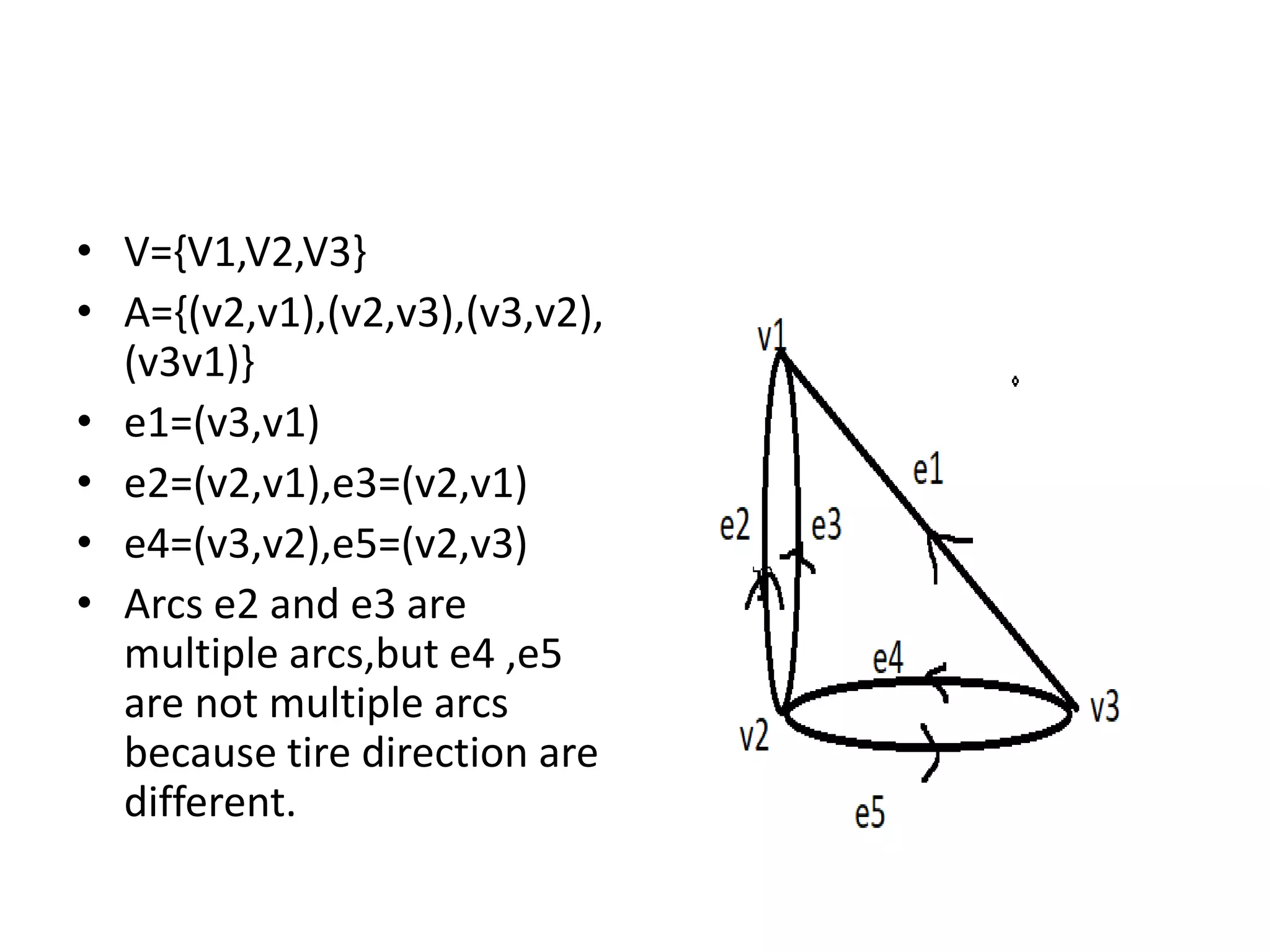
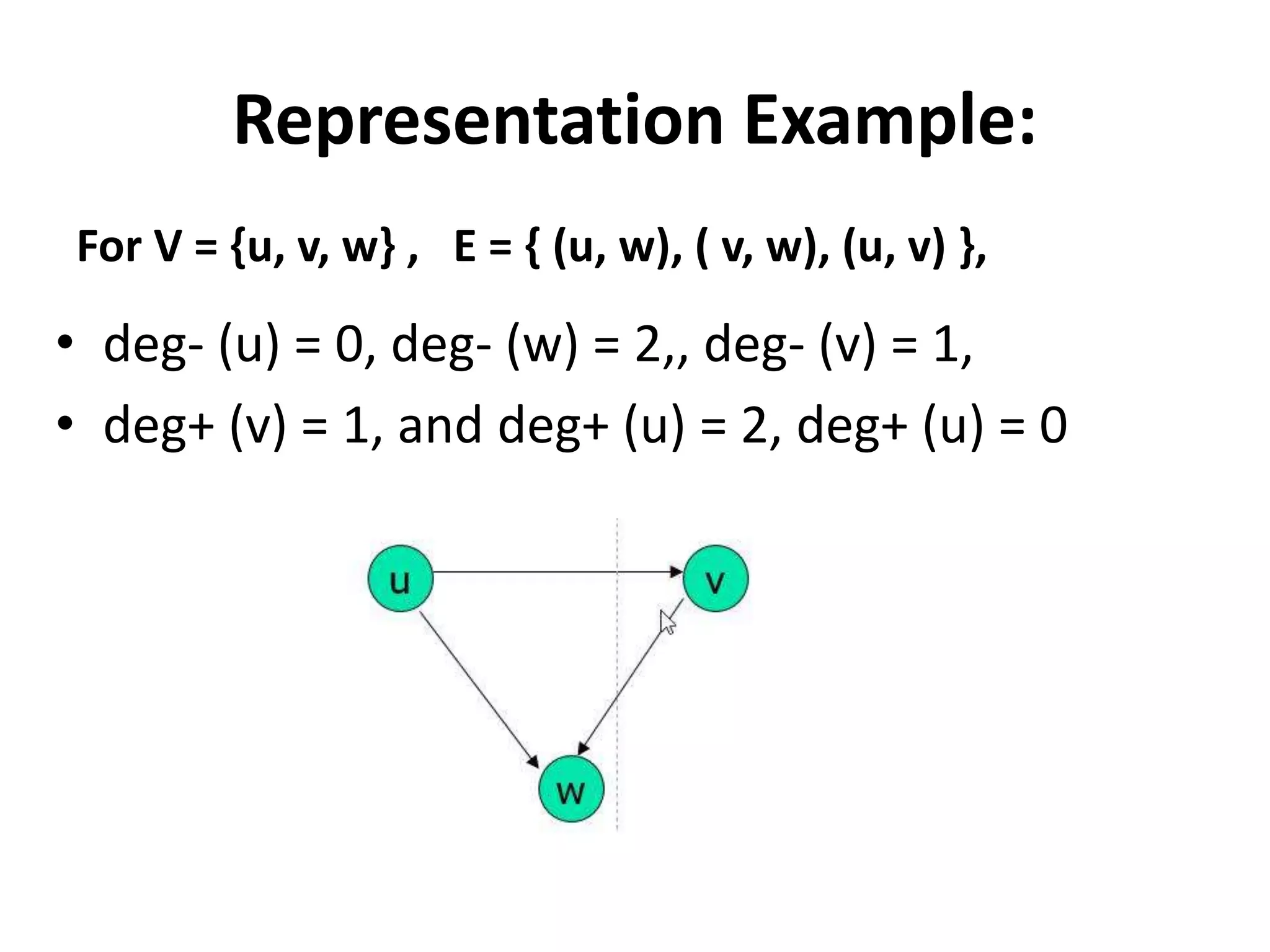
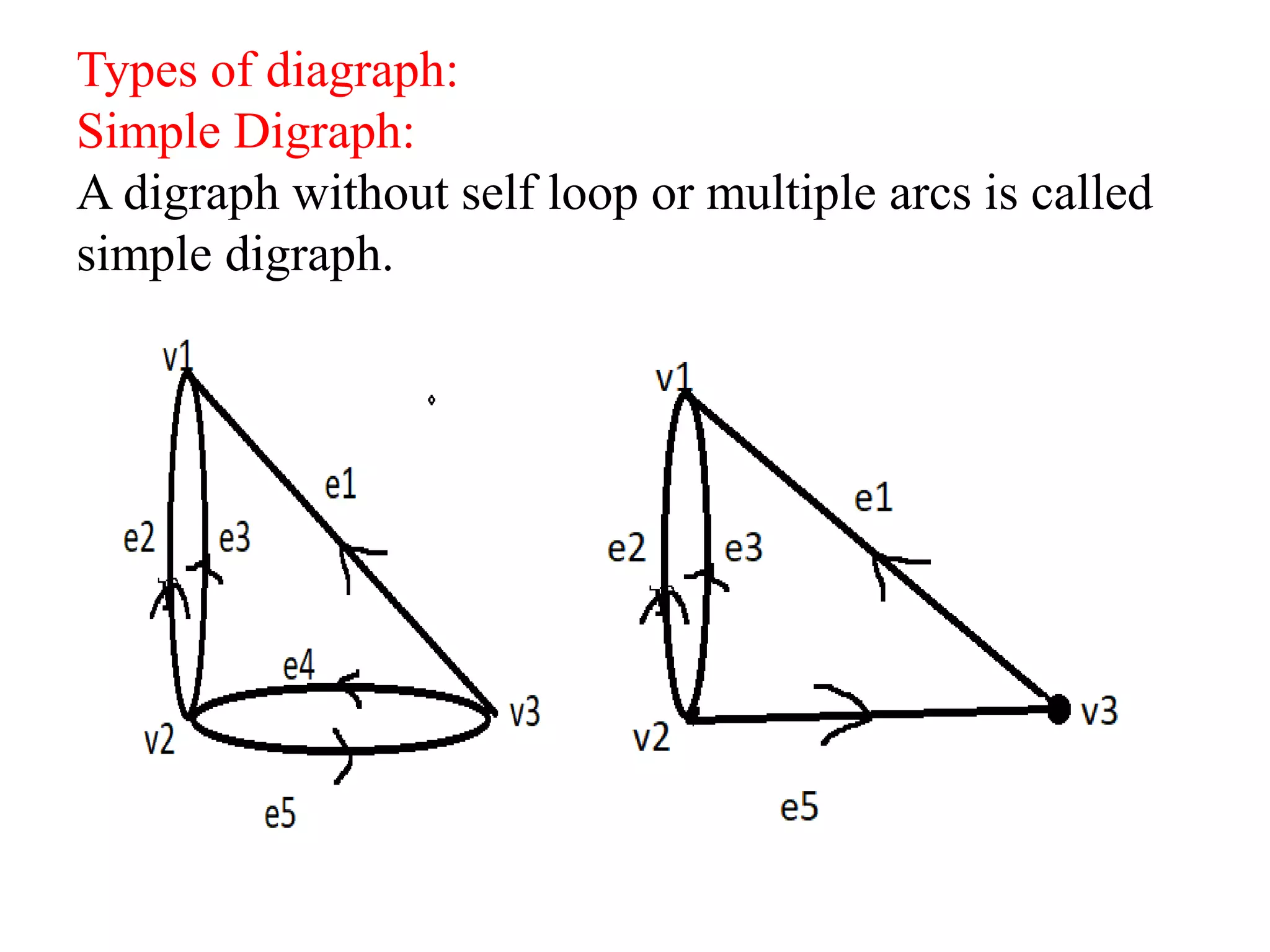
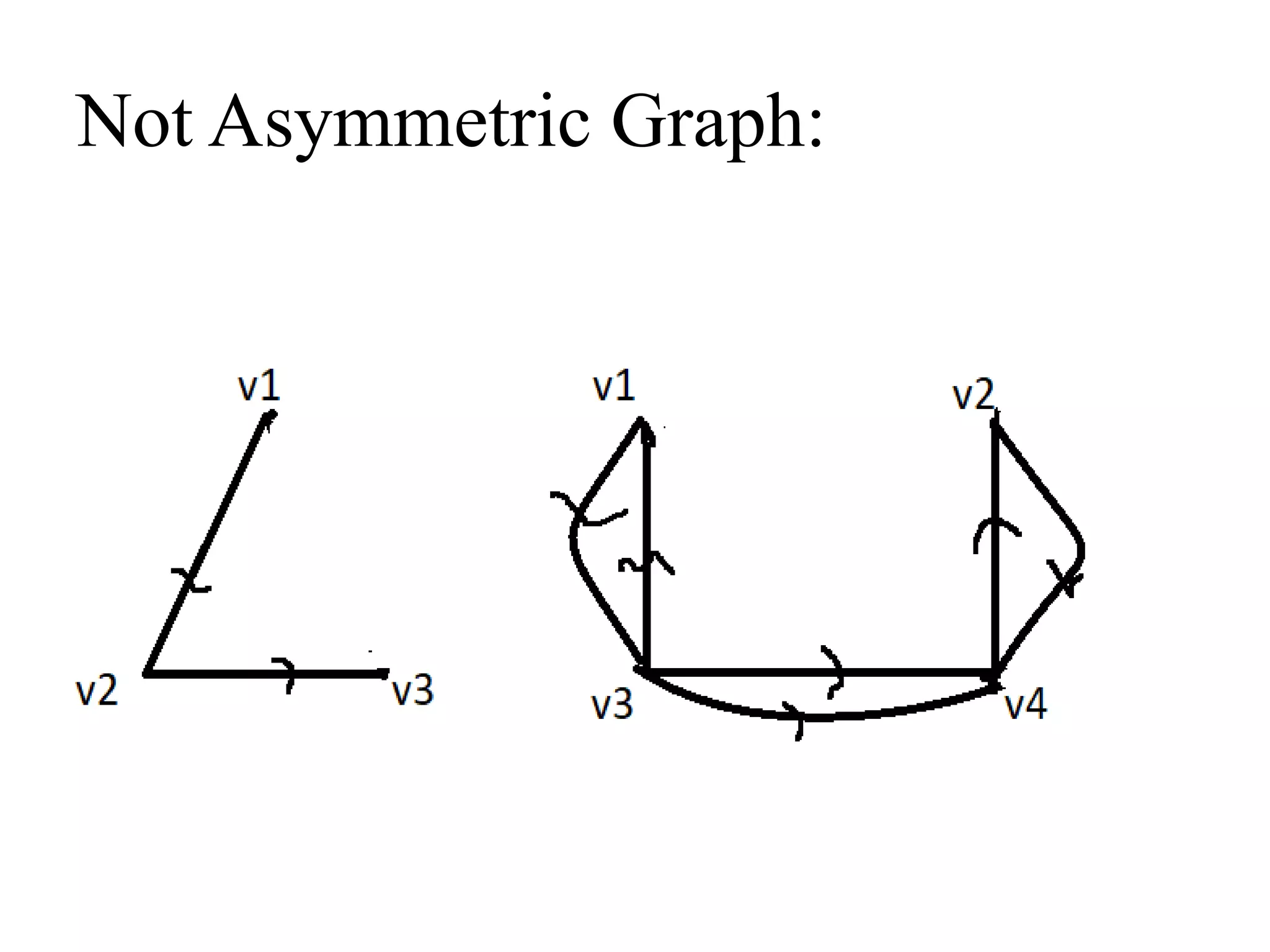
This document provides an introduction to graph theory through a presentation on the topic. It defines what a graph is by explaining that a graph G consists of a set of vertices V and edges E. It then gives examples and defines basic terminology like adjacency and incidence. The document also covers topics like degrees of vertices, regular and bipartite graphs, and representations of graphs through adjacency and incidence matrices.

1. Welcome to Mathematics
PRESENTATION
Sem II
Topics: An Introduction to Graph
Theory
Submited by:
Prof:Vidya P Bhoge.

2. Introduction
Graph
What is a graph G?
It is a pair G = (V, E),
where
V = V(G) = set of vertices
E = E(G) = set of edges
An elemnet of a set E is
generally
denoted as e=(u,v) or e=(v,u),
wherev u,v,ЄV.
Example:
V = {s, u, v, w, x, y, z}
E = {(x,s), (x,v), (x,u), (v,w), (s,v), (s,u), (s,w), (s,y), (w,y), (u,y),
(u,z),(y,z)}

3. Basic Terminology:
1)Adjacency:
-Two vertices v1 and v2 in a graph G are said to be
adjacent to each other iff they are end vertices of the
same edge e.
2) Incidence:
-If the vertex u is an end vertex of the edge e then the
edge e is said to be incident on vertex u .
Here, adjacent pairs of vertices:
{v2,v3},{v3,v4},{v2,v4} and
edge e1 is incident on vertices
v1 and v2.

4. Special edges
Parallel edges:
If Two or more edges have
same terminal vertices
then these edges are called as
parallel edges.
In the example, a and b are
joined by two parallel edges
Loop(Self loop):
If both the end vertices of an
edges are same then the edge is
called a loop.
In the example, vertex d has a
loop,e8 is loop.

5. Degree of a vertex
The degree of a vertex v, denoted by d(v), is the
number of edges incident on v
From example,
Degree of each vertex is
d(a)=4
d(b)=3
d(c)=4
d(d)=6
d(e)=4
d(f)=4
d(g)=3
Note:
If there is self loop then in the
definition of degree of vertex it is
counted twice

6. Pendant Vertex:
A vertex with degree one is called pendant vertex.
i.e deg (v) =1
Isolated Vertex:
A vertex with degree zero is called Isolated vertex.
deg (v) = 0
Representation Example:
For V = {u, v, w} ,
E = { {u, w}, (u, v) }},
deg (u) = 2, deg (v) = 1, deg
(w) = 1, deg (k) = 0,
w and v are pendant ,
k is isolated

7. Degree of the graph:
Sum of the degrees of all vertices in graph G is
called degree of the graph G.
Notation:
d(G)=degree of graph G.
d(G)= ∑ d(vi)
viЄG
i.e
d(v1)=5,d(v2)=5,d(v3)=3,
d(v4)=5,d(v5)=1,d(v6)=1
d(G)=20

8. EX: How many edges are there in a graph with
10 vertices each of degree 6?
Solution:
In graph of 10 vertices with each of degree 6.
d(G)=10X6=60
Each edge gives two degree.
Threfore,
Total number of edges in such graph=60/2=30
Therefore,G has 30 edges.

9. Hand shaking lemma:
Statement:
The sum of the degrees of all vertices
in any graph is always even number.
i.e ∑ d(v)=2.e,
vЄG
where, e= Total number of edges.

10. EX: Does there exists a party of 11
professors such that each one has exactly 7
friends in themselves?
Solution:
If we translate given situation of party in graph by
taking each professor as a vertex and thire
friendship by edges.
Then we get a graph G on 11 vertices with degree
of each vertex is 7.
i,e d(G)= 11X7=77 which is odd.
A contradiction to handshaking lemma
There does not exists such party.

11. EX: how many edges are there in the group with
8 vertices each of degree 5?
Solution : There are 8 vertices of degree 5 in a given graph
G.
Total degree of such 8 vertices
∑ d(G)= 8X5=40,
vЄG
By handshaking lemma,
∑ d(G) =2.e,
vЄG
40=2e
e=20
There are 20 edges int he graph.

12. Special graphs
• Simple graph
A graph without loops or parallel edges.
• Null Graph:
A graph with n vertices without edges.
Notation:
Nn:Null graph with n vertices.
• For e.g: . . .
N1 N2

13. Simple Graph

14. EX: Draw all possible graph graph
with 3 vertices.
• Solution:
• Graph with zero edges
• Graph with one edges
Graph with Two edges

15. Graph with 3 edges

16. Types of Graph.
Multigraph:
• A graph with parallel edges
but not loop is called Multi
graph.
Compound graph
(Pseudograph):
• A graph which contains
loops or parallel edges.

17. Fig1: Compound graph contaninig loop.
Fig:2 Compound graph contaninig loop and
parallel edges.
Fig:3Compound graph contaninig parallel
edges.

18. Complete Graph:
• Let n > 3
• A simple graph G
is called a complete graph
• if there is an edge between
every pair of vertices
• Notation:
• Kn = complete graph on n vertices
The figure represents K5

19. Properties of complete graph of n
vertices:
• Each vertex has degree (n-1).
• Number of edges=
𝑛(𝑛−1)
2

20. Complete graph

21. EX:Show that there does not exists a simple
graph with 8 vertices and 29 edges.
Solution:
Let G be a simple graph with 8 vertices.
Maximum number of edges with n vertices is
n(n-1)/2
Therefore,G has at most 8X7/2=28 edges.
Therefore,There does not exists a simple graph
with 8 vertices and 29 edges.

22. EX: Determine minimum number of vertices in a simple
graph with 30 edges.
Solution:
Let G be a simple graph with n vertices.
Maximum number of edges with n vertices are
𝑛(𝑛 − 1)
2
but G has exactly 30 edges
𝑛(𝑛−1)
2
≥30 for minimum value of n.
n(n-1)-60≥0
=>9.8-60≥0
Therefore n=9 is the minimum number of vertices for
simplegraph with 30 edges.

23. EX:Find the smallest integer n such that kn has at least
600 edges.
Solution:
Complete graph on n vertices has
𝑛(𝑛−1)
2
edges.
but the graph requires 600 edges.
𝑛(𝑛−1)
2
≥600
n(n-1)≥1200
36X35≥1200
n=36
Therefore, No of vertices of such required graph n=36

24. Regular Graph:
If all vertices of a graph G have same
degree then, G is called as a Regular
graph.
Remark: If every vertex has degree m
then G is said to be regular graph of
degree m or m- regular graph.
Notation:
mRn=-m Regular graph on n vertices

25. Regular Graph.

26. Regular Graph

27. Properties of Regular graph of n
vertices:
1) Each vertex is of same degree m
2) Number of edges= m*n/2.
3) Degree of graph d(G)= m*n.
4) Every complete graph is regular graph but
converse is not true.

28. EX: Does every regular graph
complete? Justify
Solution: Every regular graph is not complete.
Justification: We have
2R4-2regular graph with 4
vertices.But not complete graph

29. EX: Draw a 3-regular graph on 6 vertices?
EX: Draw all possible 2-regular graphs on 4 vertices.
• Solution:3-regular graph

30. Bipartite Graph
• A bipartite graph G is if the vertex set V can be
partitioned into two non empty disjoint
subsets V(G1) and V(G2) i.e such graph is
that

31. V(G1) V(G2)
• V(G) = V(G1)U V(G2),
|V( G1)| = m, |V(G2)| =n
V(G1) ∩V(G2) = φ
No edges exist between any two vertices in the same
subset
V(Gk), k =1,2

32. V={v1,v2,v3,v4}
V1={v1v3}
V2={v2,v4}

33. EX: Draw the bipartite graph which is
not regular graph.

34. Complete bipartite graph Km,n
• A bipartite graph is the
complete bipartite graph
Km,n
• if every vertex in V(G1) is
joined to a vertex in V(G2)
and conversely,
• |V(G1)| = m |V(G2)| = n
• then this bipartite graph
• complete bipartite graph
Km,n

35. Properties of complete bipertite graph
with vertex set V1 contains m vertices
and vertex set V2 contains n vertices
1) Each vertex of vertex set V1 has degree n and
each vertex of vertex set V2 has degree m.
2) Number of edges are mXn.
3) Every complete bipartite graph is bipartite but
converse is not true.i.e every bipartite graph may
not be complete bipartite.
4) d(G)=2*m*n

36. EX: Find number of edges is K5,8 graph.
Solution:
K5,8 graph is complete bipartite graph in which firest
vertex set V1 contains 5 vertices and second V2
contains 8 vertices.
Number of edges =5X8=40
EX: Find number of edges is K7,8 graph.

37. EX: Draw the following graphs
i)Non complete bipartite graph
ii) Complete graph which is complete bipartite graph.
iii)Regular graph but not complete.
iv) 3R6 i.e 3regular graph with 6 vertices.
• Solution:
Non complete bipartite
graph

38. • Complete graph which
is complete bipartite
graph
• 3R6 i.e 3regular graph
with 6 vertices.
• Regular graph but not
complete

39. EX: Daw the following graphs
i) Non complete bipartite graph
ii) Complete graph which is complete bipartite
• Solution:
• i) Non complete
bipartite graph
• Complete graph which
is complete bipartite

40. Cycle:
Graph of following structure are cycle graphs.
Notation: Cn

41. Wheels:
Wn, obtained by adding additional vertex to Cn and connecting
all vertices to this new vertex by new edges.
Representation Example: W3, W4

42. Star graph:
K1,n graph is called star graph i.e graphs of the
following form are called star graph.

43. Weighted graph:
A graph where each edge is assigned
a numerical label or “Weight”.

44. Directed graphs (Digraphs)
• G is a directed graph or
digraph if each edge has
been associated with an
ordered pair of vertices,
i.e. each edge has a
direction.

45. Terminology – Directed graphs
For the edge (u, v), u is adjacent to v OR v is
adjacent from u,
u – Initial vertex, v – Terminal vertex
In-degree (deg- (u)): The number of edges
incident into the vertex u.
Out-degree (deg+ (u)): The number of edges
incident out of a vertex u.

46. Arcs:
Directeg edges are called Arcs.
Initial Vertex:
Starting vertex of arc is called itial vertex.
Terminal Vertex:
Ending vertex of arc is called terminal vertex.
Multiple arcs:
If two vertices are joined by more than one arcs
with the same direction ,such arc are called
multiple arcs.

47. • V={V1,V2,V3}
• A={(v2,v1),(v2,v3),(v3,v2),
(v3v1)}
• e1=(v3,v1)
• e2=(v2,v1),e3=(v2,v1)
• e4=(v3,v2),e5=(v2,v3)
• Arcs e2 and e3 are
multiple arcs,but e4 ,e5
are not multiple arcs
because tire direction are
different.

48. Representation Example:
For V = {u, v, w} , E = { (u, w), ( v, w), (u, v) },
• deg- (u) = 0, deg- (w) = 2,, deg- (v) = 1,
• deg+ (v) = 1, and deg+ (u) = 2, deg+ (u) = 0

49. Remark:
1. Each arc gives one indegree to terminal vertex and
outdegree to initial vertex.
2. Sum of all indegrees of the digraph eqauls to sum
of all outdegress.
∑d-(u)=∑d+(u)
uЄv uЄv
Pendant vertex:
In a digraph a vertex having d+(u)+d-(u)=1 is called
pendant vertex.

50. Find Indegree and Outdegree of following
Digraph.
Solution:
Indegrees of v1,v2,v3 are
d-(v1)=3
d(v2)=1
d-(v3)=1
Outdegrees of v1,v2,v3 are
d+(v1)=0
d+(v2)=3
d+(v3)=2
V3 is pendant vertex.

51. Types of diagraph:
Simple Digraph:
A digraph without self loop or multiple arcs is called
simple digraph.

53. Non simple Digraphs:

54. Symmetric Digraph:
A digraph D is called symmetric if for every directed
edge (a,b) in D ,then there must be directed edge (b,a)
in D is called as symmetric digraph.
• For.e.g

55. Simple Symmetric digraph:
A digraph which is both simple and symmetric is called
simple symmetric digraph

56. Asymmetric digraph:
A digraph D in which there exists at the most one
directed edge between evry pair of vertices with may
or may not self-loop is called asymmetric digraph.

57. Not Asymmetric Graph:

58. Balanced Digraph:
Digraph D is balanced digraph if for every vertex ,the number
of indegrees equals to number of outdegress d+(v)=d-(v) for
all vertex is called Balanced digraph.
Regular Digraph:
A balanced digraph in which
outdegree and indegree of each
vertex is same then such digraph
is called regular digraph.
d-(v1)=1 d+(v1)=1
d+(v2)=1
d(v2)=1

59. Definitions – Graph Type

60. Representations of graphs
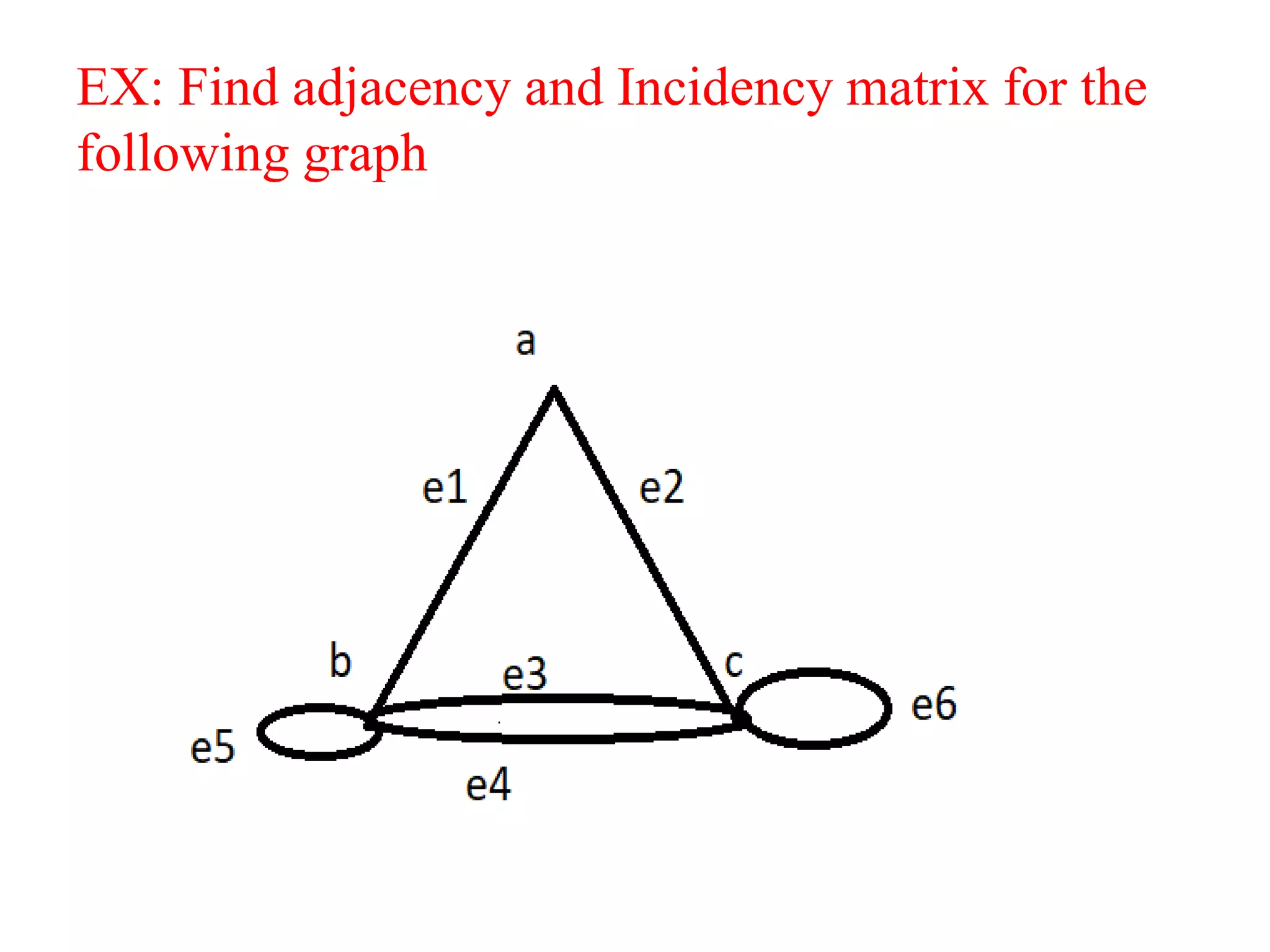
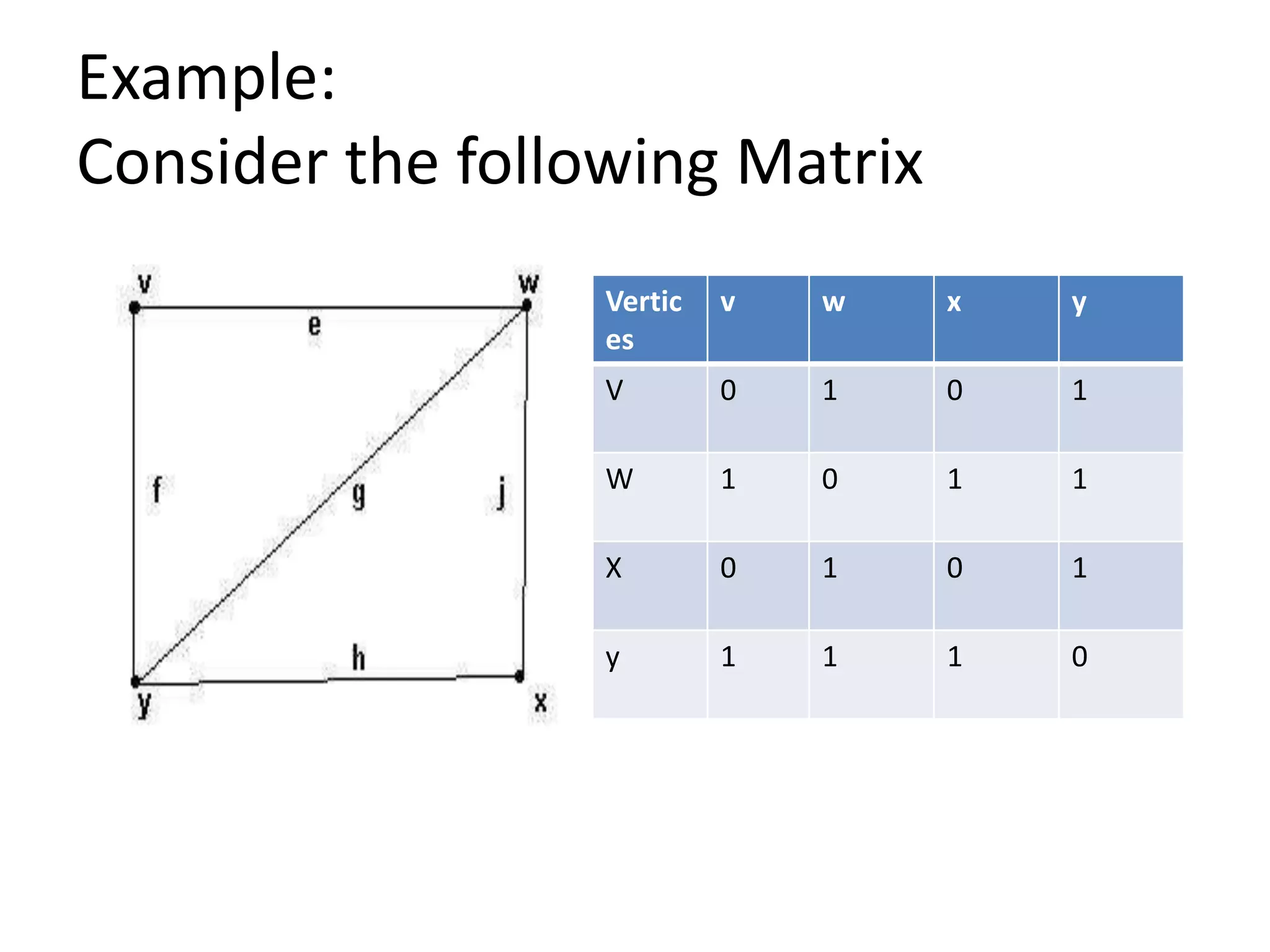
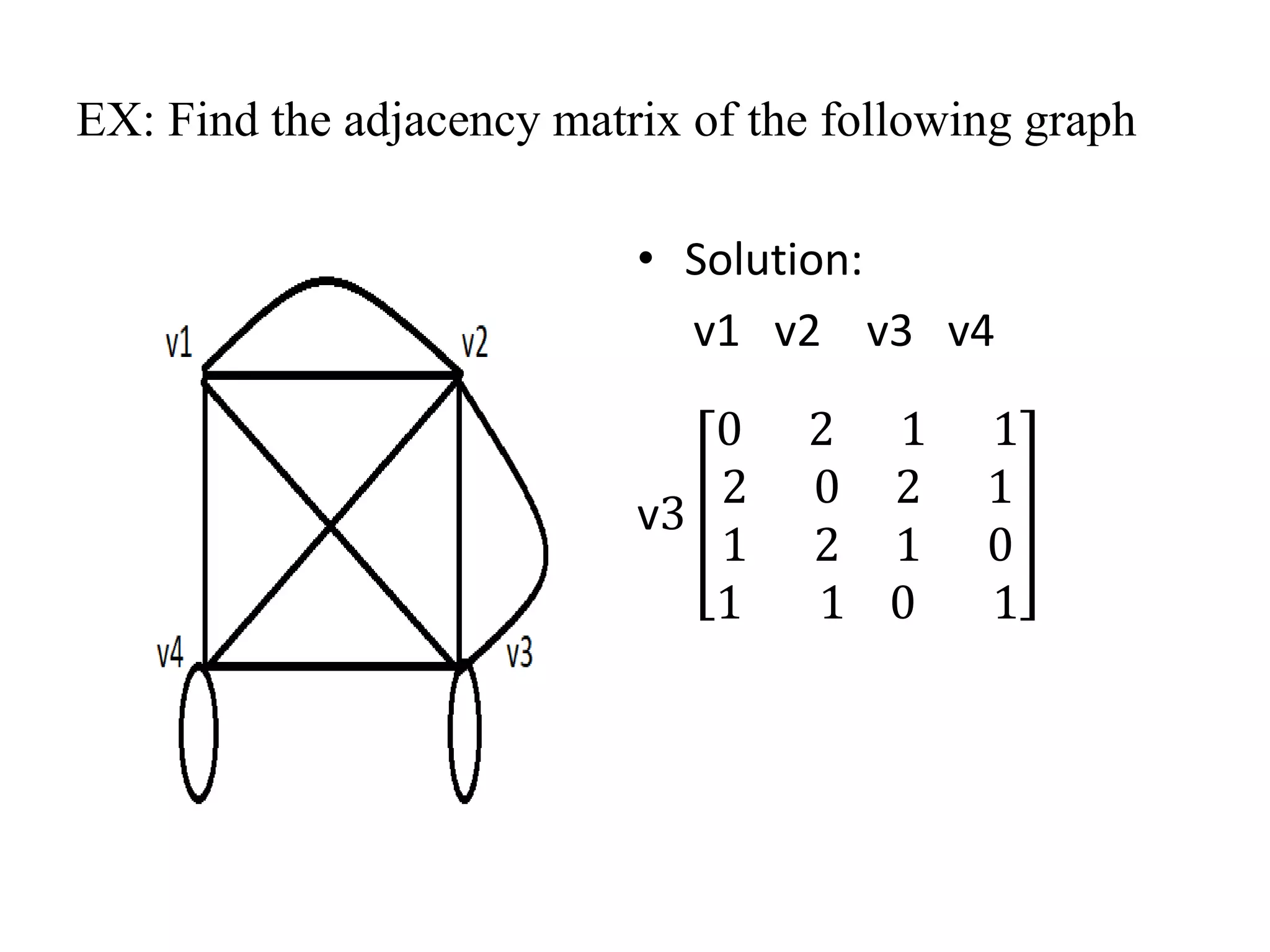
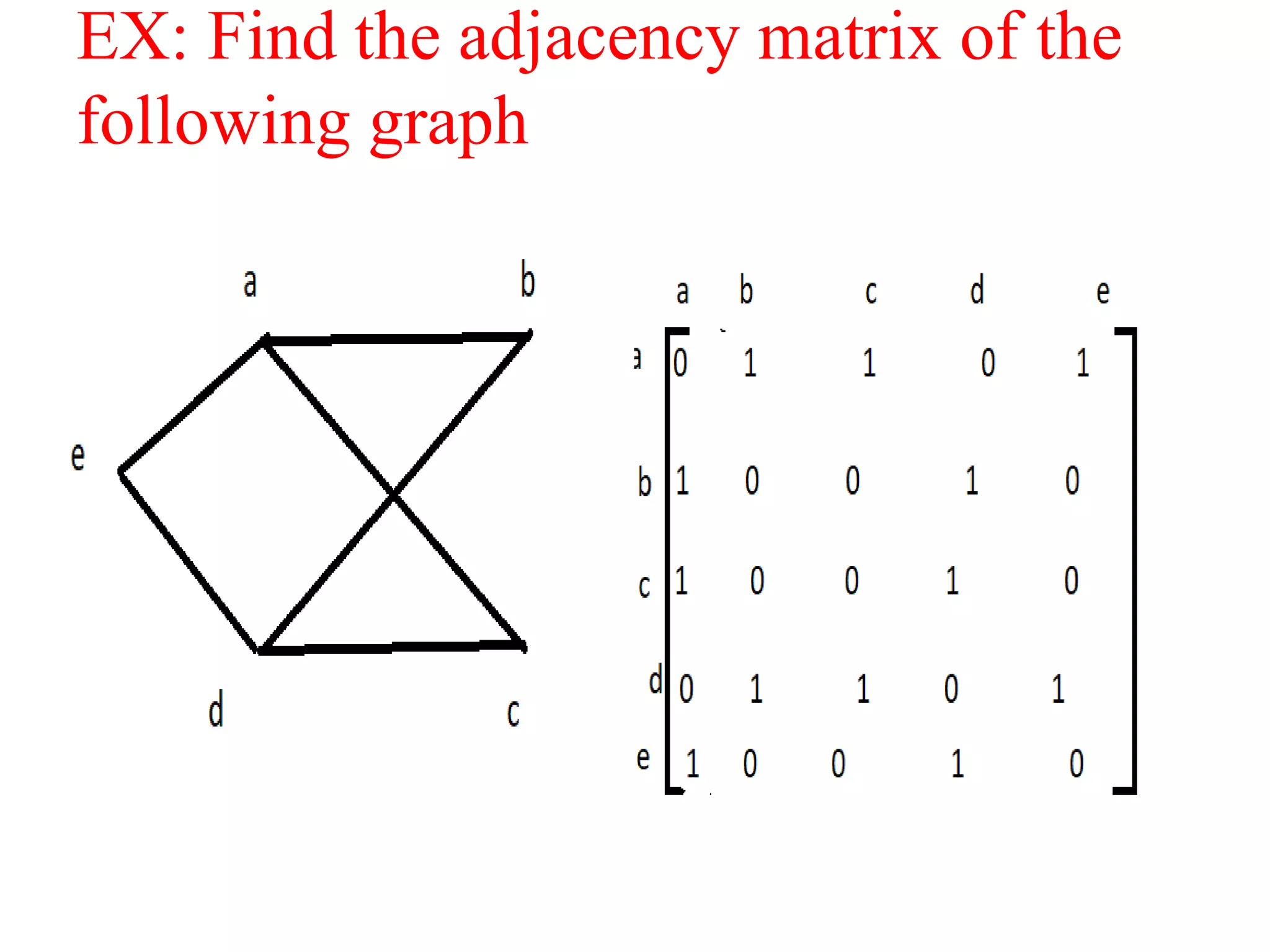
Adjacency matrix:
Definition:
If G is a graph on n vertices say v1,v2…vn then
adjacency matrix of G is the nXn matrix
A(G)=[aij]nxn
Where,
aij= number of edges between vi and vj.
=1 for self loop

61. -Rows and columns are labeled with
ordered vertices
-write a 1 if there is an edge between the
row vertex and the column vertex
and
0 if no edge exists between them

62. Example:
Consider the following Matrix
Vertic
es
v w x y
V 0 1 0 1
W 1 0 1 1
X 0 1 0 1
y 1 1 1 0

63. EX: Find the adjacency matrix of the following graph
• Solution:
v1 v2 v3 v4
v3
0 2 1 1
2 0 2 1
1 2 1 0
1 1 0 1

64. EX: Find the adjacency matrix of the
following graph

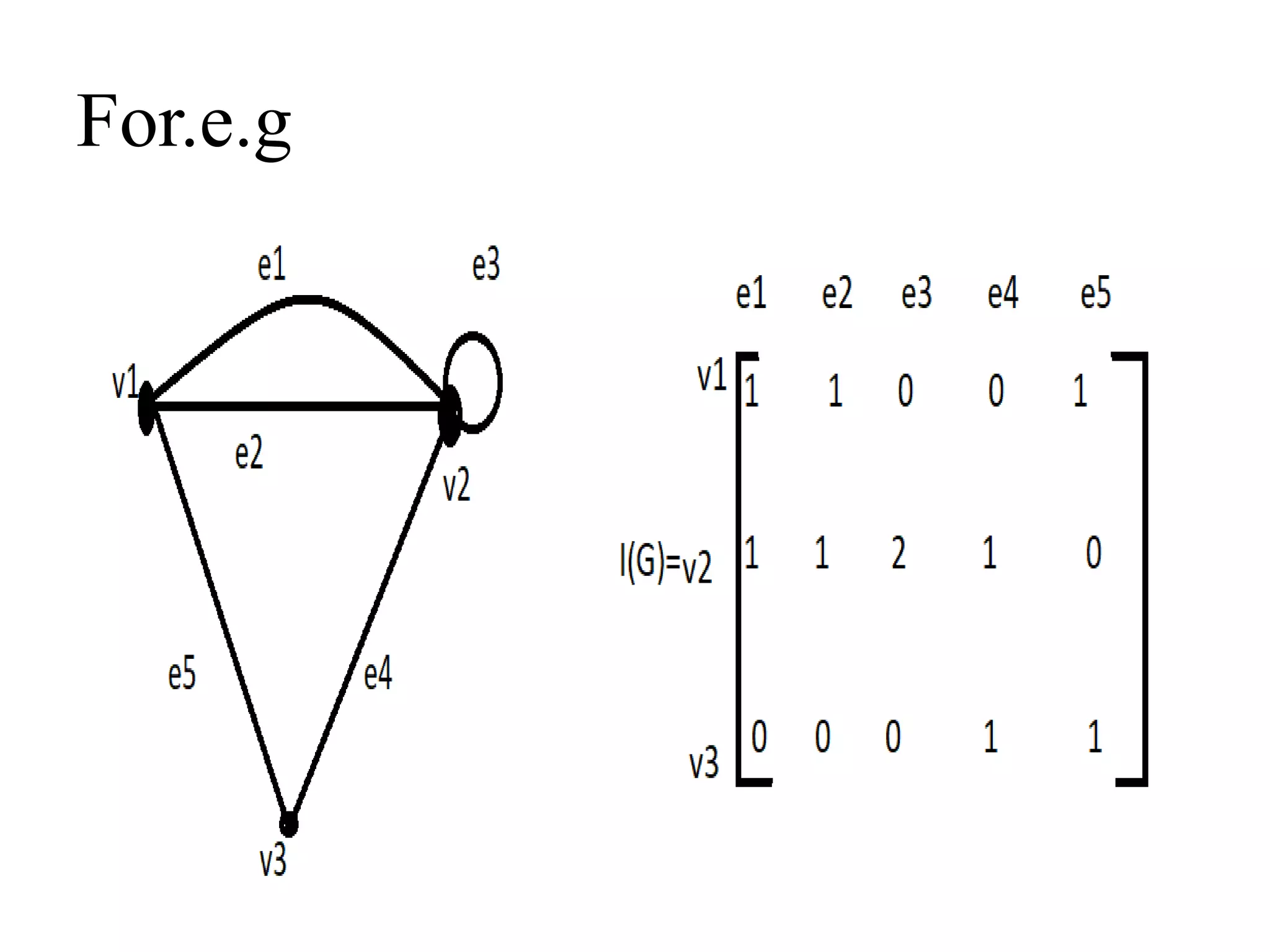
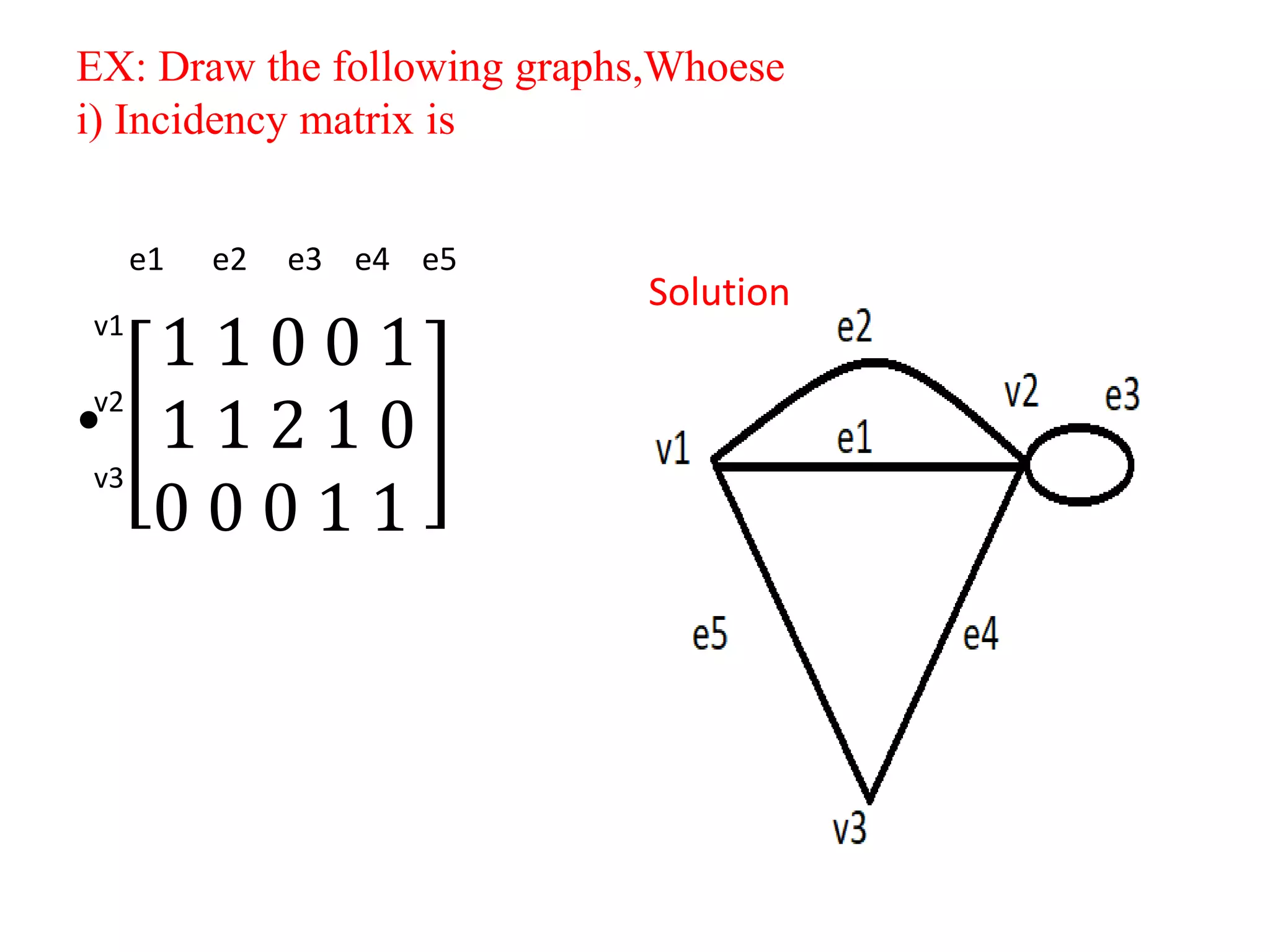
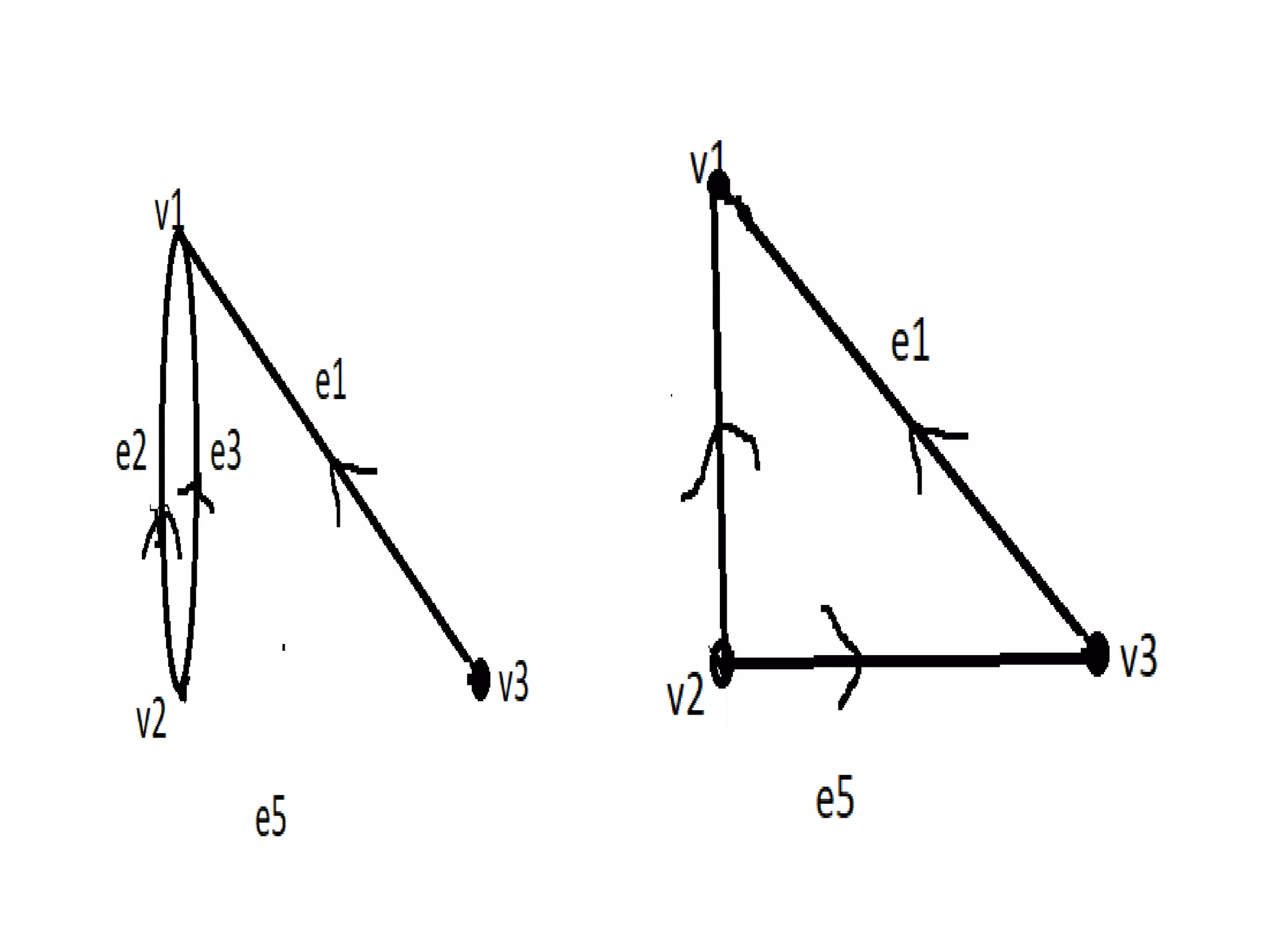
65. Incidence matrix:
Let G be a graph with n vertices v1,v2,v3...,vn and
m edges e1,e2,..,em then the incidencematrix G is
denoted by I(G) as,
I(G)=[aij]nXm where,
aij=
0 𝑖𝑓 𝑣𝑖 𝑖𝑠 𝑛𝑜𝑡 𝑖𝑛𝑐𝑖𝑑𝑒𝑛𝑡 𝑤𝑖𝑡ℎ 𝑒𝑗
1 𝑖𝑓 𝑣𝑗 𝑖𝑠 𝑖𝑛𝑐𝑖𝑑𝑒𝑛𝑡 𝑤𝑖𝑡ℎ 𝑒𝑗
2 𝑖𝑓 𝑒𝑗 𝑖𝑠 𝑎 𝑙𝑜𝑜𝑝 𝑎𝑡 𝑣𝑖

66. For.e.g

67. Observations:
• Each column contains exactly two 1’s.
• The sum of the entries in a row indicates the
degree of the corresponding vertex.
• If two columns are identical,then the
corrosponding edges are parrellel edges.
• If a row contains only zero’s then the
corrosponding vertex must be an isolated vertex.
• If a row contains a sing1,s the corresponding
vertex must be pendant vertex.
• If an edge is a loop there will be a single ‘2’ in the
column remaining entries being zero’s.

68. EX: Draw the following graphs,Whoese
i) adjacency matrix is
•
0 1 0 1 0 1
1 0 1 0 0 1
0 1 0 1 1 1
1 0 1 0 0 0
0 0 1 0 0 0
1 1 1 0 0 0

70. EX: Draw the following graphs,Whoese
i) Incidency matrix is
•
1 1 0 0 1
1 1 2 1 0
0 0 0 1 1
e1 e2 e3 e4 e5
v1
v2
v3
Solution

71. EX: Find adjacency and Incidency matrix for the
following graph

72. Isomorphism of graphs:
Definition:
Let G1(V1,E1) and G2(V2,E2) be two graphs.The
graphs G1 and G2 are said to be isomorphic if there is
bijective functions fV:V1->V2 and fE:E1->E2 such that
if u and v are end vertices of some edge e ЄE1 then
fv(u),fv(v) are end vertices of fE(e).
EX: Draw all posible non isomorphic simple graphs
with 4 vertices?
Solution:
Graph of zero edges:

73. Graph of 1 edges:
Graph of 2 edges:
Graph of 3 edges:
Graph of 4 edges:

74. Graph of 5 edges:
Graph of 6 edges:
Graph of 7 edges:

75. EX: Determine if the following are isomorphic.

76. Number of vertices in G1 =8=number of vertices in
G2
Number of Edges in G1 =10=number of Edges in G2
In graph G1
Vertex Degree Degree of adjacent
vertices
a 3 3,2,2
b 2 3,3
c 3 2,3,2
d 2 3,3
e 3 3,2,2
f 2 3,3
g 3 3,2,2
h 2 3,3

77. In graph G2
Vertex Degree Degree of
adjacent vertices
p 3 3,3,2
q 3 2,3,3
r 2 3,2
s 2 2,3
t 3 2,3
u 2 3,2
v 2 3,2
w 3 2,3,2

78. From above table we say that in G1 vertex with
degree 3 having degree of adjacent vertex are
3,2,2 does not exist in G2.
Therefor,G1 is not isomorphic to G2.

79. EX: Show that the following graphs are
isomorphic?

80. Number of vertices in G1 =8=number of vertices in
G2
Number of Edges in G1 =10=number of Edges in G2
In graph G1
Vert
ex
Degree Degree of
adjacent
vertices
v1 4 3,2,2,3
v2 3 4,2,2
v3 2 4,3
v4 2 3,3
v5 2 4,3
v6 3 4,2,2
Vert
ex
Degre
e
Degree of
adjacent
vertices
u1 4 2,2,3,3
u2 2 4,3
u3 2 4,3
u4 3 4,2,2
u5 3 4,2,2
u6 2 3,3

81. From above table a bijection between
vrtices of G1 and G2 is
f(v1)=u1
f(v2)=u4
f(v3)=u3
f(v4)=u6
f(v5)=u2
f(v6)=u5
Therefore,G1 and G2 are isomorphic.