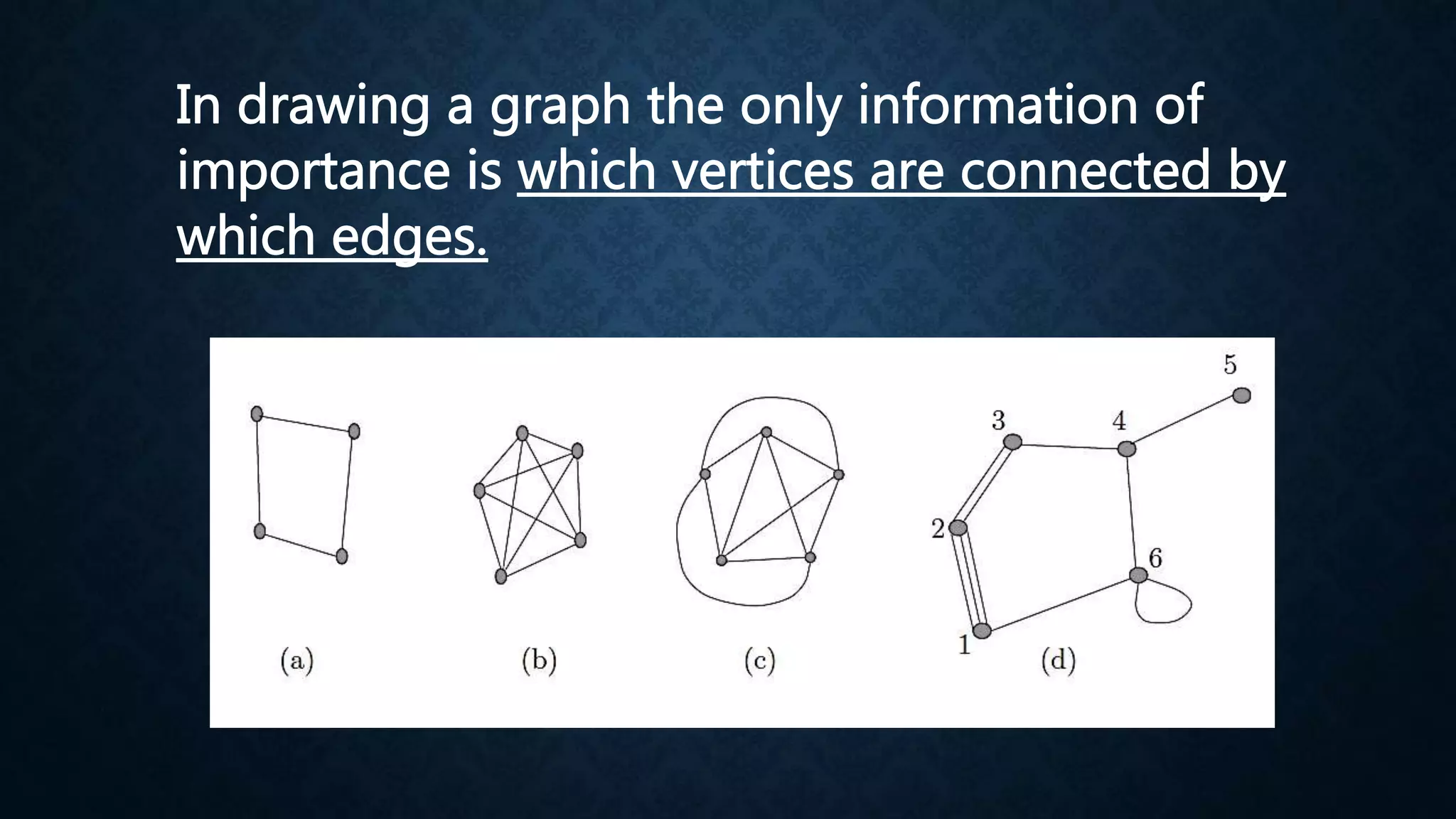
This document discusses graph theory and Leonhard Euler's solution to the Königsberg bridge problem in the 18th century. It explains that a graph will contain an Euler path if it contains at most two vertices of odd degree, and will contain an Euler circuit if all vertices have even degree. An example is given of a police officer wanting to patrol a neighborhood while walking as little as possible, which relates to finding an Euler circuit in a graph.

1. GRAPH
THEORY

5. THE SEVEN BRIDGES OF
KÖNIGSBERG, GERMANY

6. Leonhard Euler
Konigsberg Bridge Problem

10. A
B
C
D
A
B
C
D

11. A
BC
D E

12. Degree 0 Degree 1 Degree 2 Degree 3 Degree 4

13. A graph will contain an Euler path if it contains at most two vertices of odd degree.
A
B C D
EF F
A B C
DE

14. A graph will contain an Euler circuit if all vertices have even degree.
A
B C D
EF A
B C D
E
F
G

15. Why do we care an Euler circuit exist. For example the police officer wanted to
patrol on a neighborhood on walking as little as possible. The ideal would be a
circuit that covers every street with no repeats. That's an Euler circuit! Luckily Euler
solved the question of whether or not an Euler path or circuit will exist.

16. Thanks