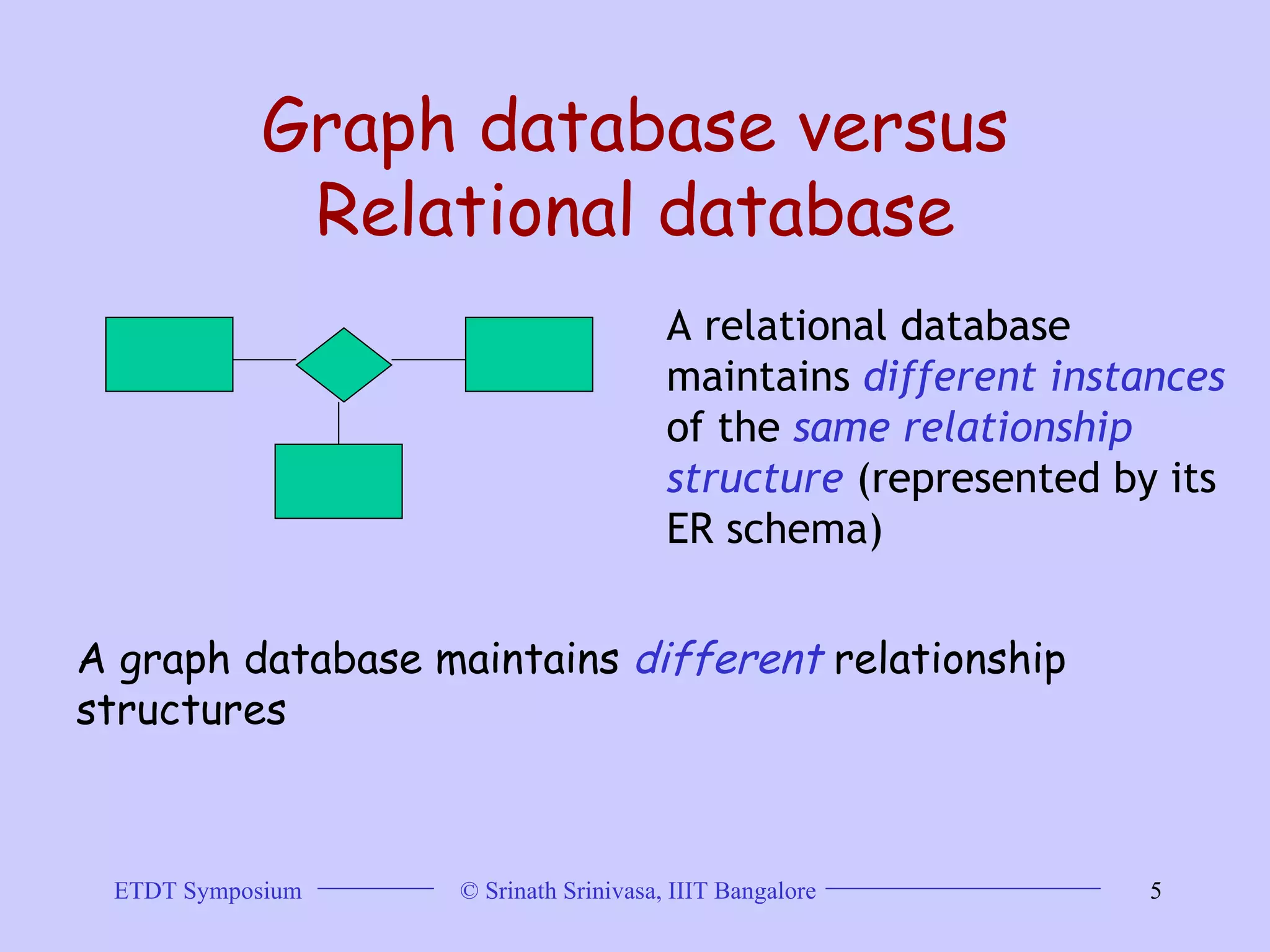
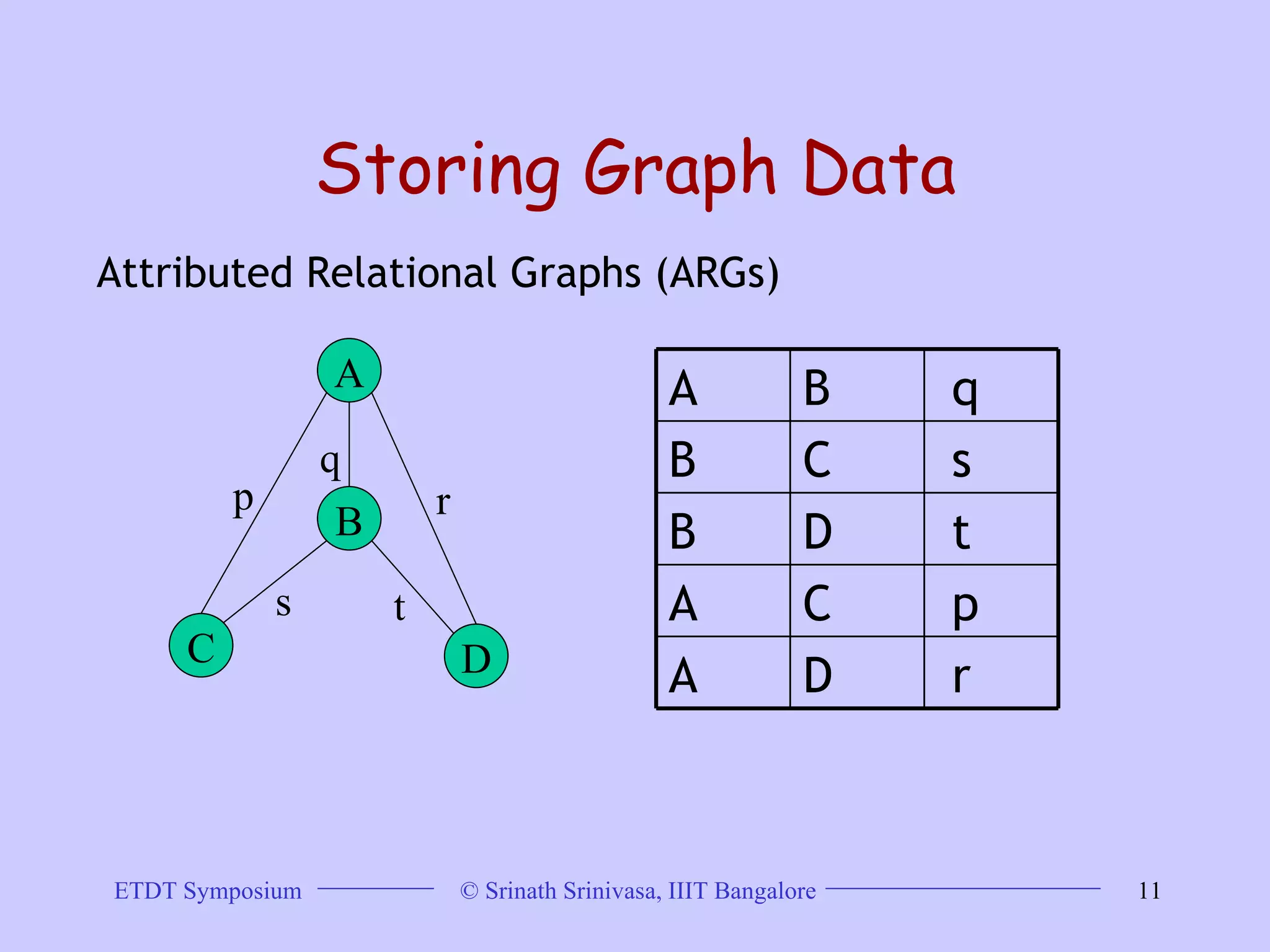
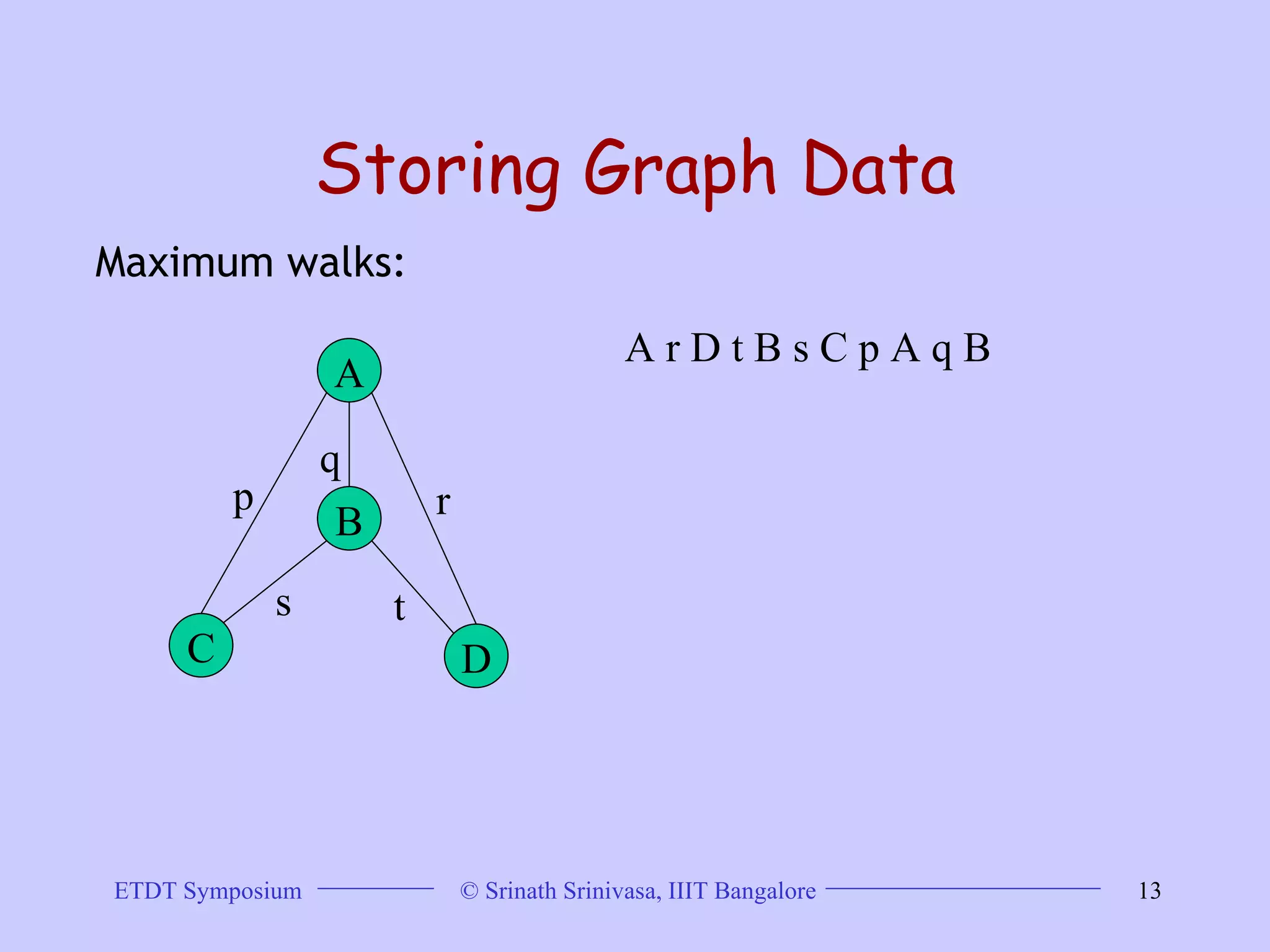
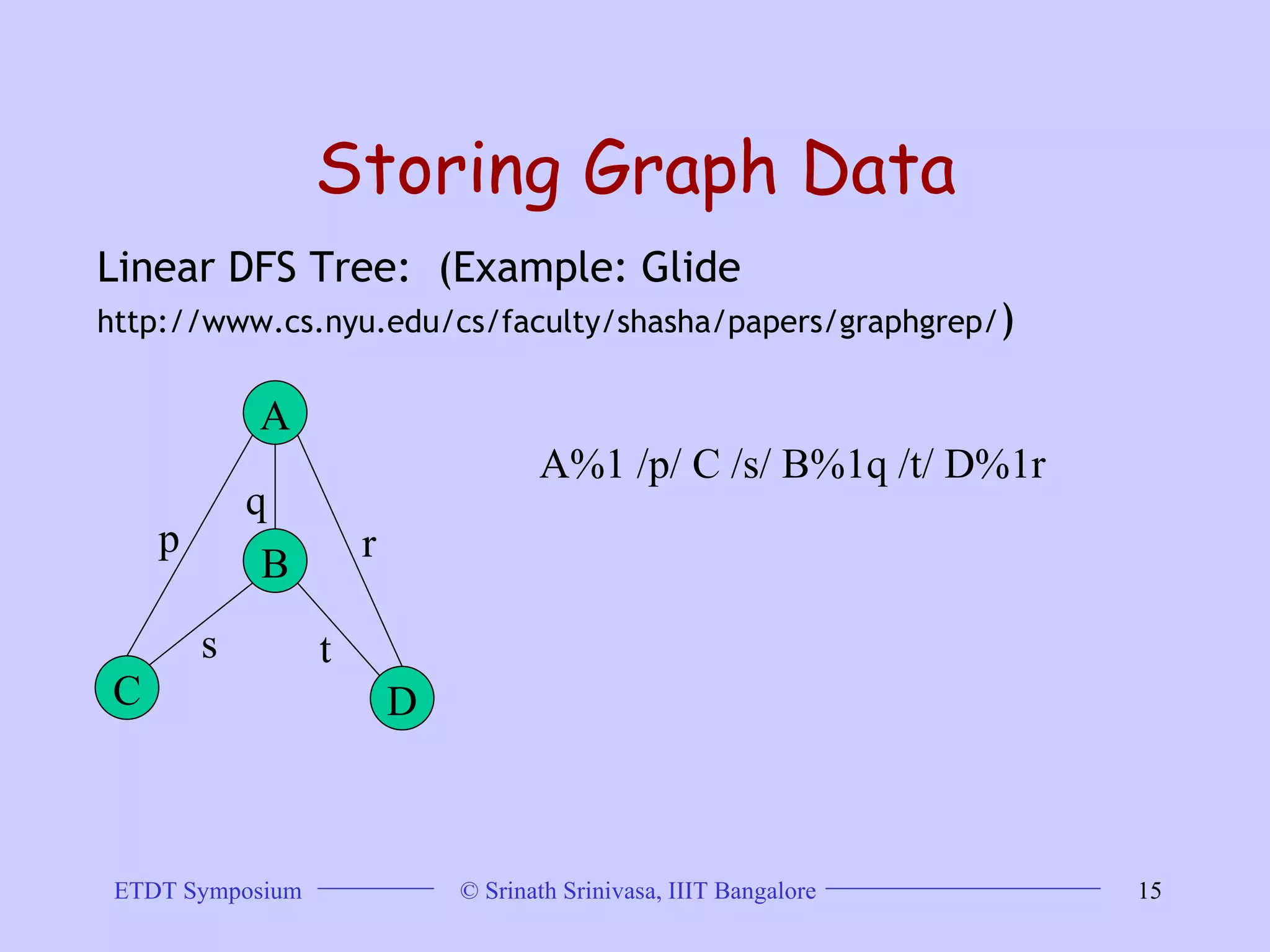
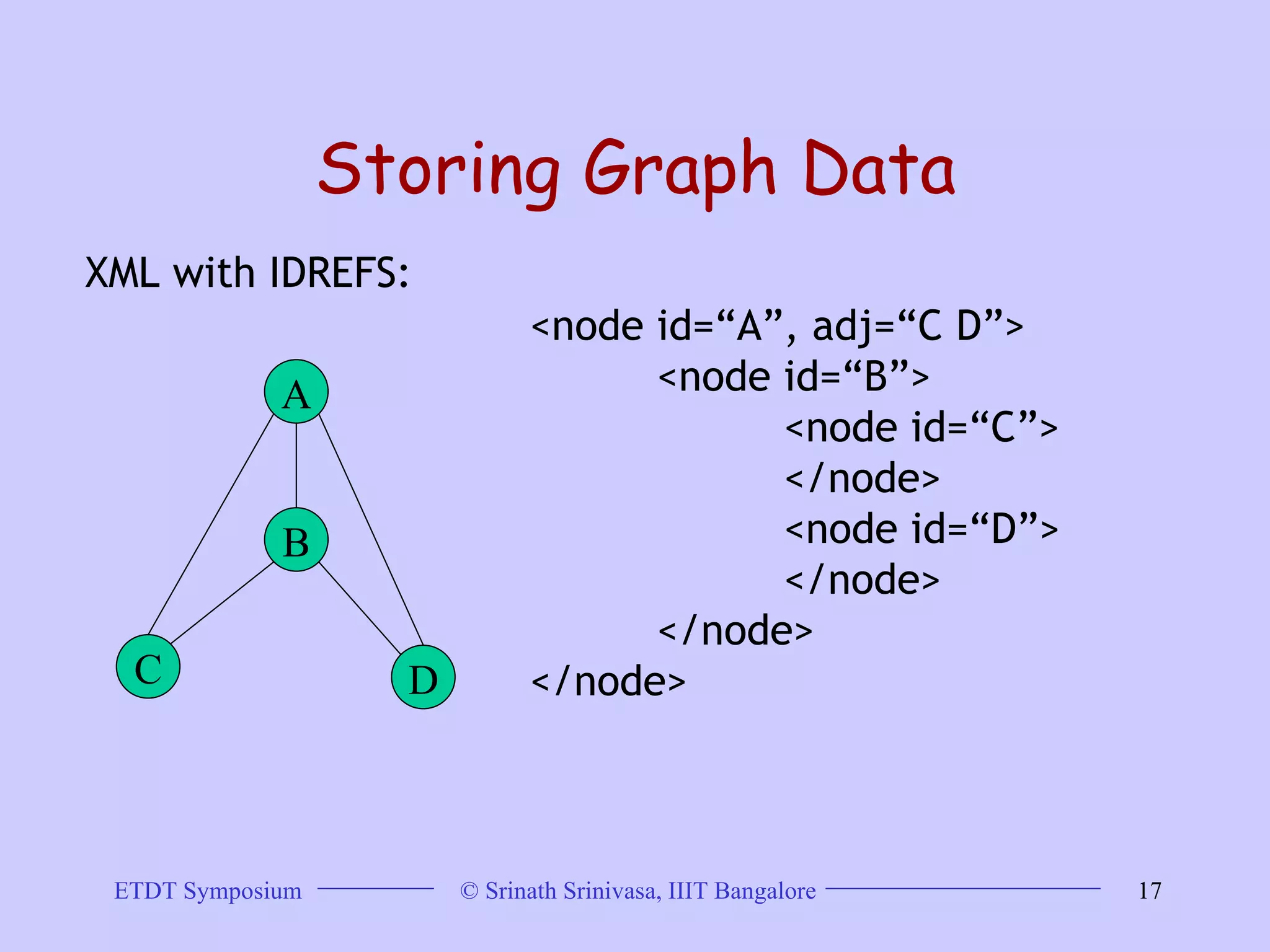
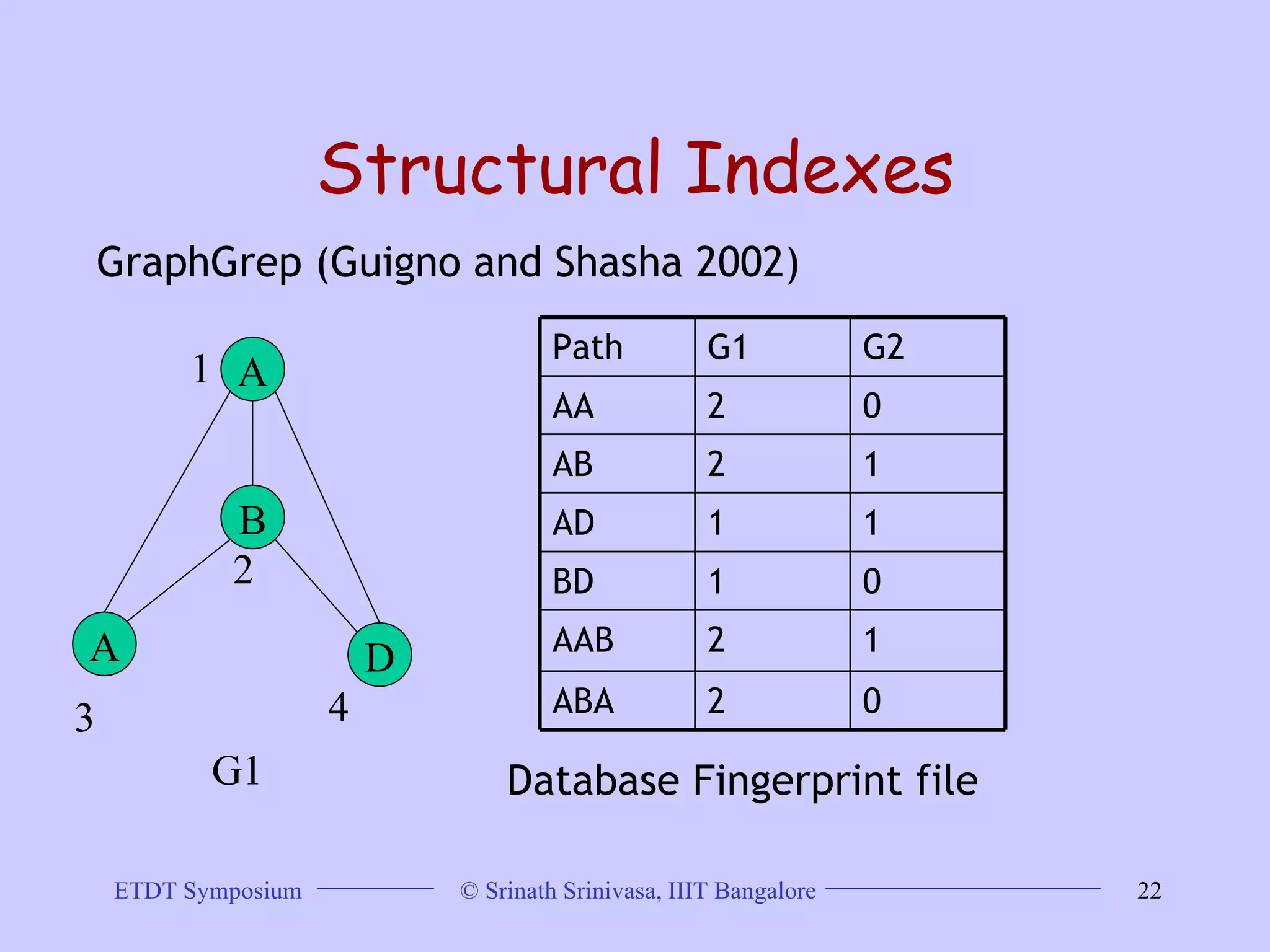
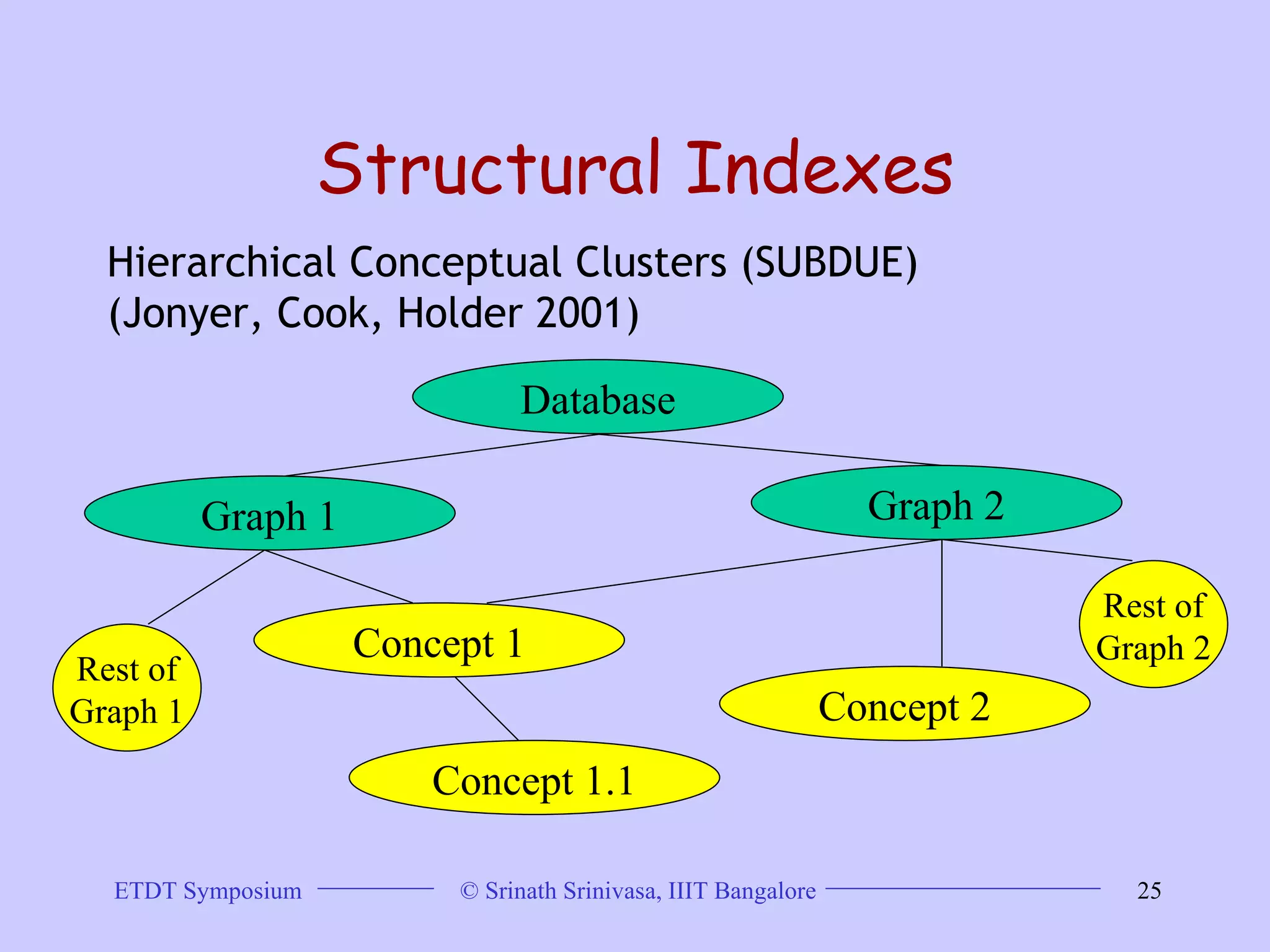
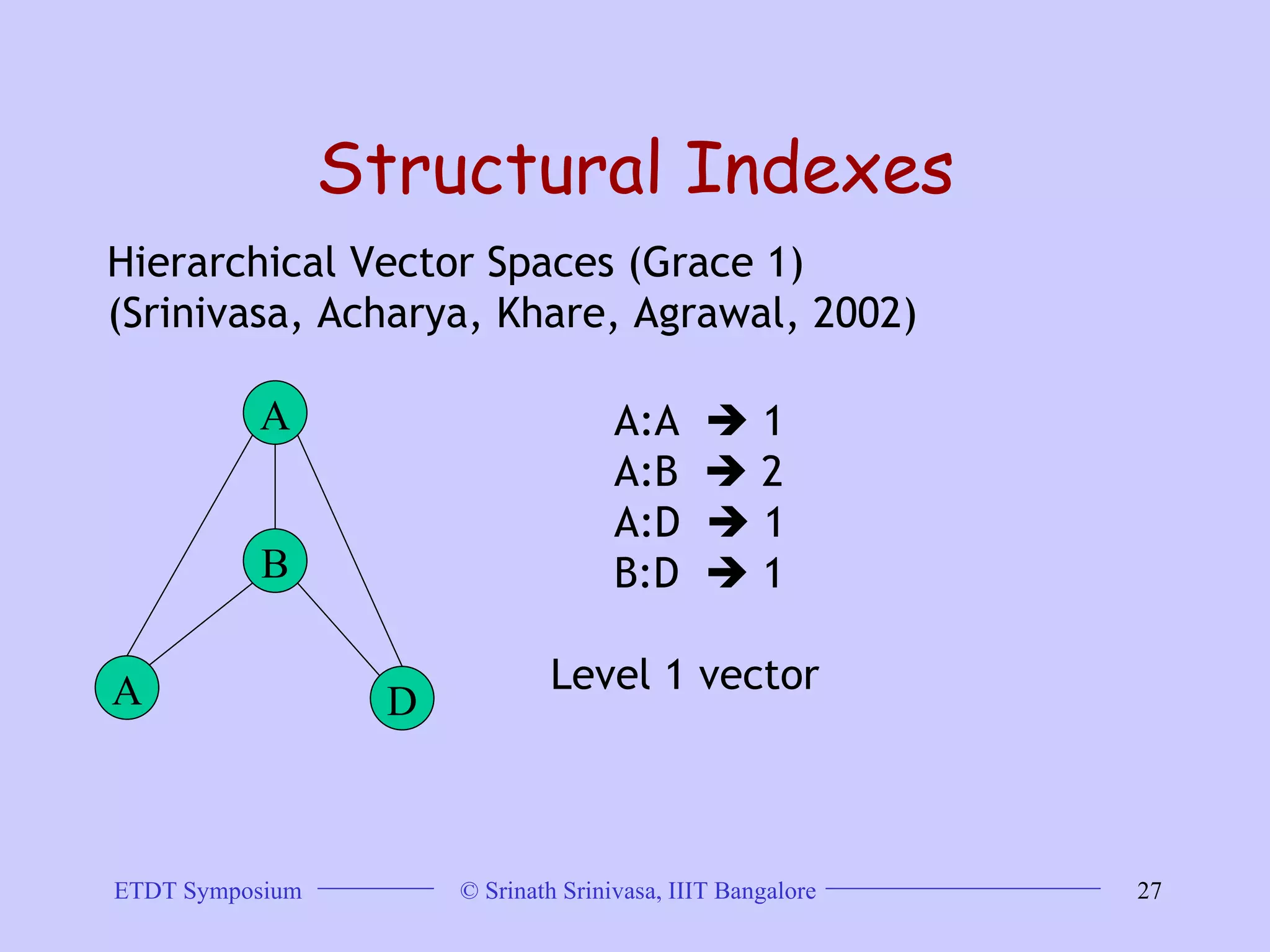
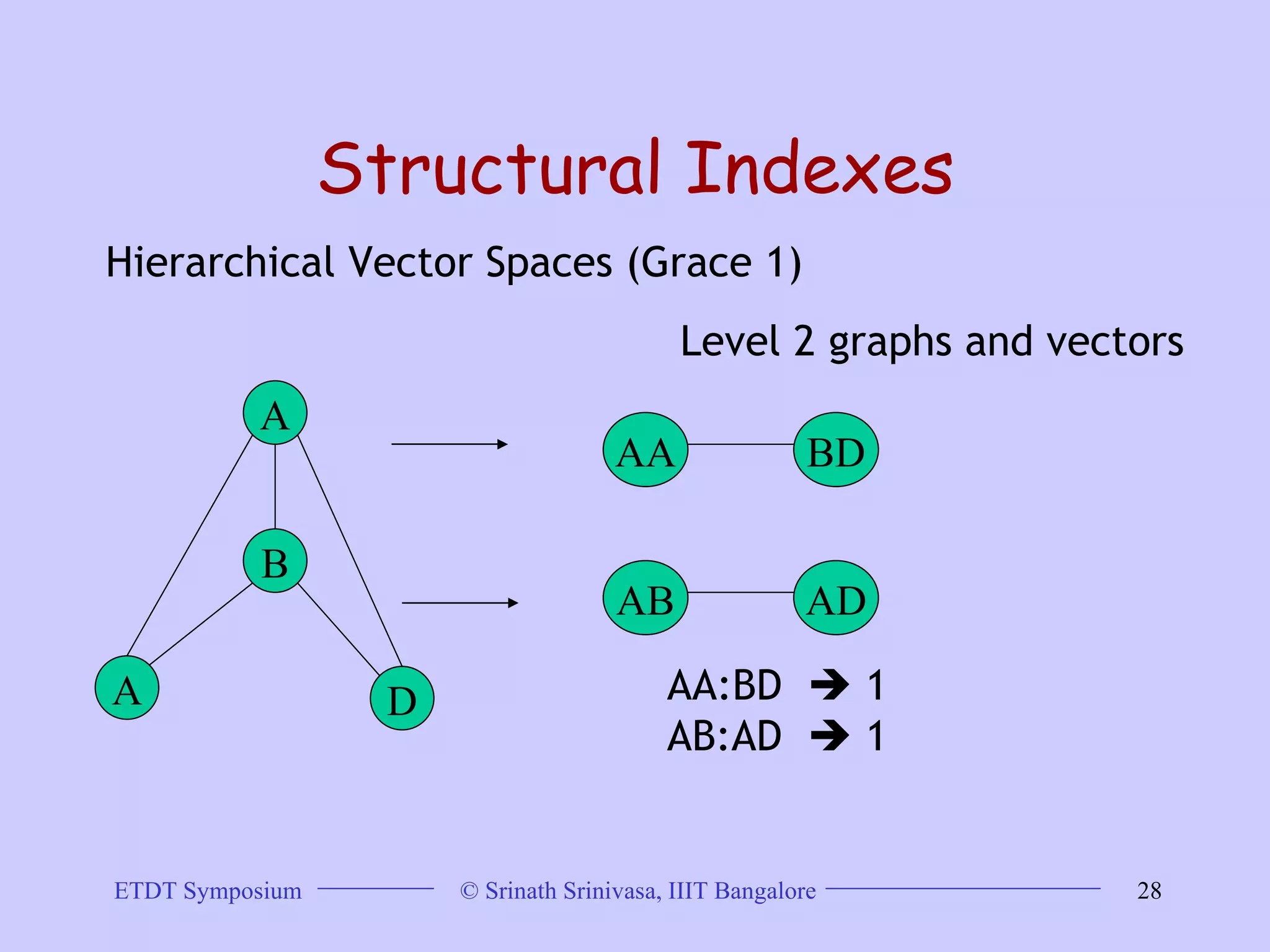
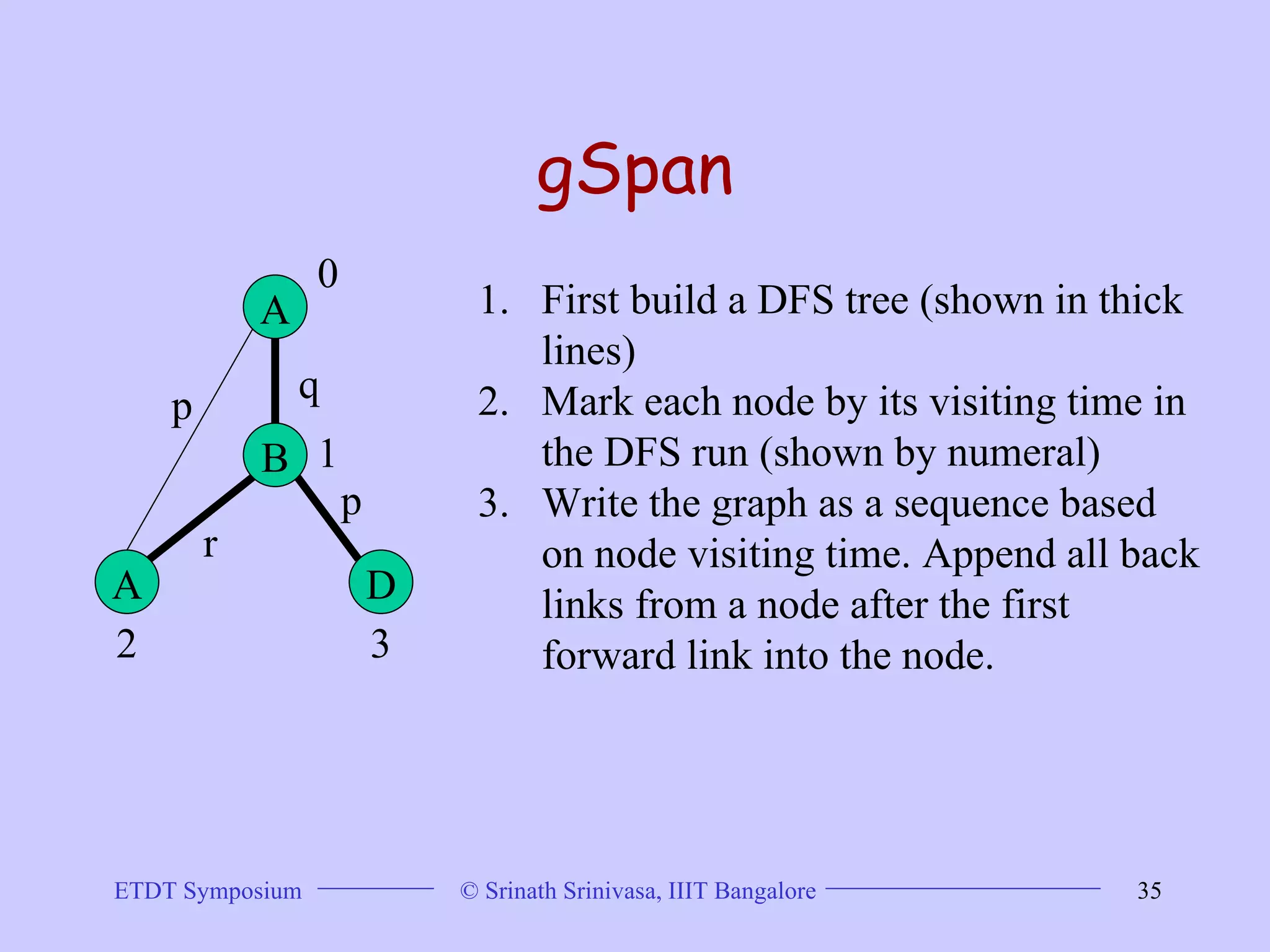
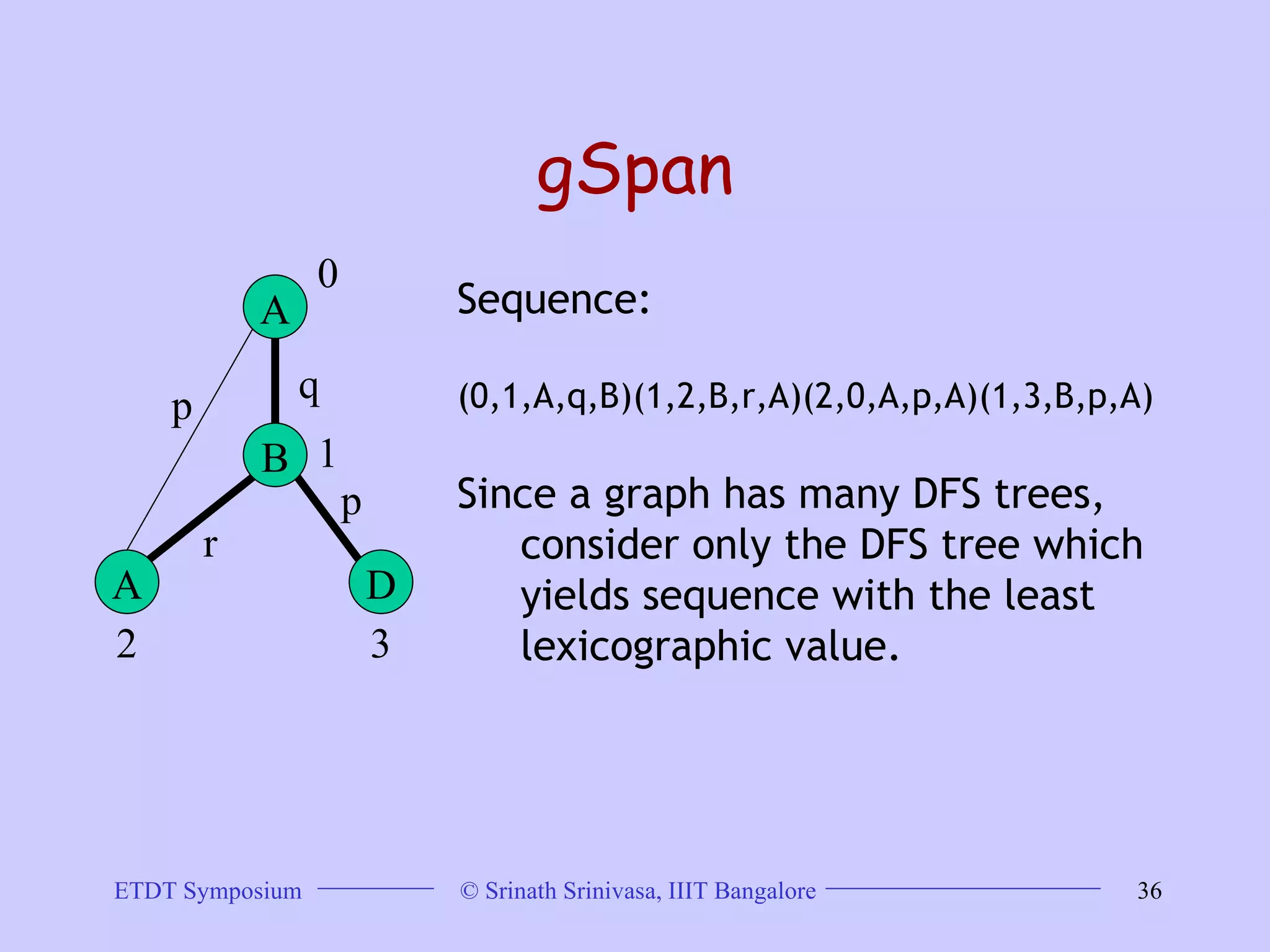
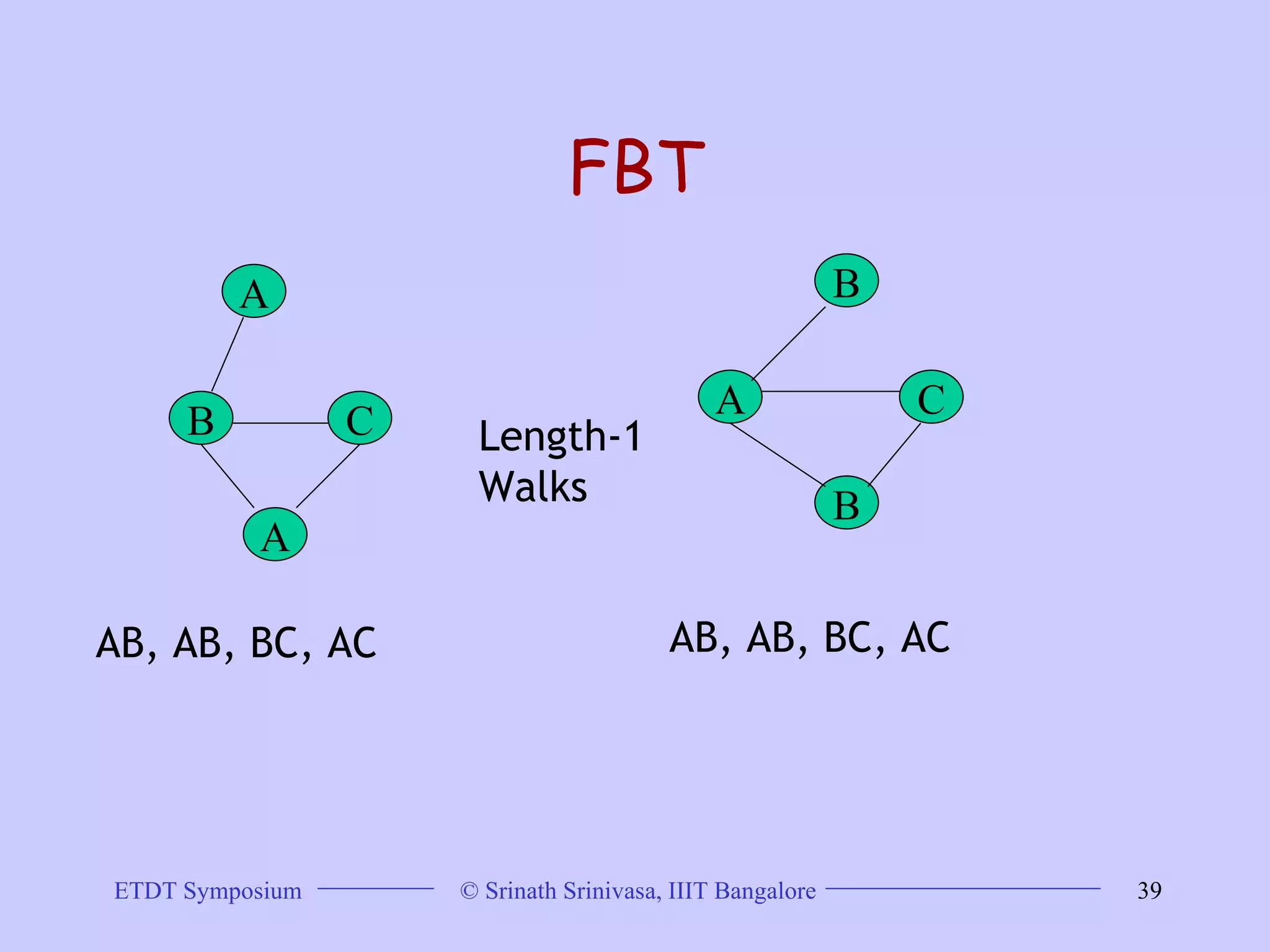
This document discusses trends in graph data management and mining, highlighting the characteristics of graph databases compared to relational databases. It covers various storage models, querying methods, and structural indexes for efficient data retrieval, along with mining frequent subgraphs using techniques like gspan and filtration-based approaches. Applications span various fields, including bioinformatics and software engineering, emphasizing the importance of effective graph representation and querying strategies.

1. Trends in Graph Data Management and Mining Srinath Srinivasa IIIT Bangalore [email_address]

2. No data is an island…

3. Outline Graph Data and its characteristics Structural Queries Storage Models for Graphs Data Models for Graph Databases Structural Indexes Mining Frequent Subgraphs gSpan FBT

4. Graph Data A graph G = (V,E) is a collection of nodes (vertices) and edges. A graph represents a “relationship structure” among different data elements. A graph database is a collection of different graphs representing different relationship structures.

5. Graph database versus Relational database A relational database maintains different instances of the same relationship structure (represented by its ER schema) A graph database maintains different relationship structures

6. Graph Database Applications Software Engineering UML diagrams, flowcharts, state machines, … Knowledge Management Ontologies, Semantic nets, … Bioinformatics Molecular structures, bio-pathways, … CAD Electrical circuits, IC designs, … Cartography, XML Bases, HTML Webs, …

7. Queries over Graph Databases Attribute Queries Queries over attributes and values in nodes and edges. Equivalent to a relational query within a given schema Structural Queries Queries over the relationship structure itself. Examples: Structural similarity, substructure, template matching, etc.

8. Structural Queries on Graph Data Undirected Graphs Structural similarity, substructure Directed Graphs Structural similarity, substructure, reachability Weighted Graphs Shortest paths, “best” matching substructure Labeled Graphs Labeled structural similarity, unlabeled structural similarity

9. Structural Queries Substructure query Given a graph database G = {G 1 , G 2 , … G n } and a query graph Q, return all graphs G i where Q is a subgraph of G i . Structural similarity Given a graph database G = {G 1 , G 2 , … G n } and a query graph Q and a threshold t, return all graphs G i where the edit distance between Q and G i is at most t. The edit distance between two graphs is the number of edge modifications (additions, deletions) required to rewrite one graph into the other

10. Structural Queries (Sub)graph isomorphism is believed to be neither in P nor in NP-complete In graph databases structure matching has to be performed against a set of graphs! Proper storage, pre-processing and index structures crucial if structural searches are to be practical

11. Storing Graph Data Attributed Relational Graphs (ARGs) A B C D p q r s t r D A p C A t D B s C B q B A

12. Storing Graph Data ARGs ARGs store a graph as a set of rows, each depicting an edge Amenable to storage in an RDBMS and easy attribute searches using SQL Costly structural searches, requiring complex nesting of SELECT statements Each graph needs a separate table

13. Storing Graph Data A B C D p q r s t Maximum walks: A r D t B s C p A q B

14. Storing Graph Data Maximum walks Stores all walks of maximum possible length in the graph Traversable graphs stored as a single sequence Easy to answer attribute queries and reachability queries Non-traversable graphs need multiple sequences Variable record length for sequences Significant pre-processing time for reducing graph to the best set of sequences

15. Storing Graph Data Linear DFS Tree: (Example: Glide http://www.cs.nyu.edu/cs/faculty/shasha/papers/graphgrep/ ) A B C D p q r s t A%1 /p/ C /s/ B%1q /t/ D%1r

16. Storing Graph Data Linear DFS Tree A sequence form of depth-first traversal of the graph Suitable for any kind of undirected graphs (but not necessarily for directed graphs) Suitable for attribute queries Some techniques proposed for substructure queries over linear DFS trees Large pre-processing time

17. Storing Graph Data XML with IDREFS: A B C D <node id=“A”, adj=“C D”> <node id=“B”> <node id=“C”> </node> <node id=“D”> </node> </node> </node>

18. Storing Graph Data XML with IDREFS Reduces graph database to an XML base Use XPath / XQuery engines for structural queries Widely supported by a variety of XML parsers Costly structure/sub-structure matching Needs distinction between IDREF edges and hierarchy edges

19. Graph Database Models “ Schema-less” collection of graphs Example: GraphGrep, Daylight ACD, gIndex Database as a graph Example: SUBDUE Database with schema and views Example: GRACE

20. Structural Indexes Used for fast structure-based retrieval of graphs Primarily meant for labeled undirected graphs Usually support substructure and structural similarity searches May either return exact matches (NP-complete) or inexact matches based on heuristics (P)

21. Structural Indexes GraphGrep (Guigno and Shasha 2002) Two index files: “ Fingerprint” file holding label-paths “ Path” file holding id-paths … paths from length 1 up to a maximum l p

22. Structural Indexes GraphGrep (Guigno and Shasha 2002) A B A D 1 2 3 4 G1 Database Fingerprint file 0 2 ABA 1 2 AAB 0 1 BD 1 1 AD 1 2 AB 0 2 AA G2 G1 Path

23. Structural Indexes GraphGrep (Guigno and Shasha 2002) A B A D 1 2 3 4 G1 Database Paths file {1-2-3, 3-2-1} ABA {1-3-2, 3-1-2} AAB {2-4} BD {1-4} AD {1-2, 3-2} AB {1-3, 3-1} AA G1 Path

24. Structural Indexes GraphGrep Stores all paths in member graphs up to a maximum length Signature file narrows search space Exact substructure matching possible when node id in query matches node id in member graphs Exponential preparation time Running time increases exponentially as max path length increases

25. Structural Indexes Hierarchical Conceptual Clusters (SUBDUE) (Jonyer, Cook, Holder 2001) Database Graph 1 Graph 2 Concept 1 Concept 2 Rest of Graph 1 Rest of Graph 2 Concept 1.1

26. Structural Indexes Hierarchical Conceptual Clusters Clusters the database into commonly occurring substructures Database is organized as a hierarchical index Clustering based on substructures that perform “best compression” by reducing graph description length Number of clusters may increase exponentially Compression / search time significant

27. Structural Indexes Hierarchical Vector Spaces (Grace 1) (Srinivasa, Acharya, Khare, Agrawal, 2002) A B A D A:A  1 A:B  2 A:D  1 B:D  1 Level 1 vector

28. Structural Indexes Hierarchical Vector Spaces (Grace 1) A B A D Level 2 graphs and vectors AA BD AB AD AA:BD  1 AB:AD  1

29. Structural Indexes Hierarchical vector spaces Hashes a graph onto vectors in a hierarchy of vector spaces Higher level graphs are formed by replacing edges (vectors) of lower level by nodes Compression of a graph may lead to several higher level graphs Fast structural similarity searches; but based on inexact matching View explosion anomaly during refinement

30. Structural Indexes gIndex (Yan, Yu, Han, 2004) Mine database for frequent substructures (using gSpan) Maintain index structure containing (size, substructure) pairs Increase minsup as the size of the indexed substructure increases

31. Structural Indexes gIndex (Yan, Yu, Han, 2004) Given a query graph q: Mine database along with q, and determine all frequent substructures F in q Reduce search space to all graphs containing all frequent substructures of F Perform graph matching against all graphs in the reduced search space

32. Graph Mining Given a database of graphs find all frequently occurring substructures in the database

33. Notes on Frequent Item-set Mining The Apriori algorithm is useful for mining frequent item-sets from transaction logs Apriori is based on the fact that in order to construct a frequent L item-set it is sufficient to know only the set of all frequent L-1 item-sets Apriori property holds for frequent subgraphs However, apriori algorithm on a graph database requires several sub-graph isomorphism checks!

34. Apriori Based Graph Mining Strategy for Apriori-based graph mining Use a re-write strategy to represent all graphs in the database as a unique sequence Substructure search reduces to a sub-sequence search Use AprioriAll (Apriori for sequences) to mine the database Best known rewrite mechanism to date is proposed in gSpan.

35. gSpan A B A D p q r p 0 1 2 3 First build a DFS tree (shown in thick lines) Mark each node by its visiting time in the DFS run (shown by numeral) Write the graph as a sequence based on node visiting time. Append all back links from a node after the first forward link into the node.

36. gSpan A B A D p q r p 0 1 2 3 Sequence: (0,1,A,q,B)(1,2,B,r,A)(2,0,A,p,A)(1,3,B,p,A) Since a graph has many DFS trees, consider only the DFS tree which yields sequence with the least lexicographic value.

37. Filtration Based Technique (FBT) Proposed by Srinivasa and BalaSundaraRaman (Submitted after first revision to IEEE TKDE) Opposite of Apriori construction on graphs but equivalent to Apriori on walks Starts with an assertion that all graphs in the database are isomorphic Filters away all edges that contradict such an assertion Algorithm converges to the maximal common (frequent) subgraph.

38. Filtration Based Technique (FBT) Filtration is based on enumerating label-walks in the graphs. Label walks accentuate differences between graphs as the length of the walks increase…

39. FBT A B C A B A C B Length-1 Walks AB, AB, BC, AC AB, AB, BC, AC

40. FBT A B C A B A C B Length-2 Walks ABA , ABC, BCA, BAC, ABA, ACB ABC, ACB, BCA, BAC, BAB , BAC

41. FBT i = 1 Enumerate walks of length i from member graphs and organize them into different buckets based on label sequence Discard buckets that don’t have minsup i++ Remove as intermediate results all graphs that don’t have walks of length i Go to step 2 until no more walks exist

42. FBT Very fast convergence, but can find only maximal common substructures If two or more common substructures overlap, FBT cannot separate the substructures Applied successfully to carcinogen dataset from US NTP, protein structures from PDB and Web traversal logs from Yahoo.

43. GRACE2 and Safari Second version of GRACE Supports a query algebra for graph queries, views, and dynamic schemas Query language called Safari

44. GRACE2 Data Model Member graphs Node, edge and graph attributes The “default” graph Schema graphs and meta-graphs

45. Safari Constructs selectin <cond> <graphref> Use graphref as a schema and return a view of the schema based on cond selecton <cond> <graphref> Search for cond within graph referred by graphref and return a subgraph selectgraph <cond> <graphref> Retrieve graph matching cond from the schema or meta-graph referred by graphref. If more than one graph matches cond, another view is returned.

46. References I. Jonyer, D.J. Cook, L.B. Holder. Graph-Based Hierarchical Conceptual Clustering. Journal of Machine Learning Research, Vol 2, 2001. Rosalba Guigno, Dennis Shasha. GraphGrep: A Fast and Universal Method for Substructure Searches. Proc of ICCV 2002. Srinath Srinivasa, Sumit Acharya, Rajat Khare, Himanshu Agrawal. Vectorization of Structure for Indexing Graph Databases. Proc of IASTED Int’l Conf on Information Systems and Databases, ISDB 2002, Tokyo, Japan. Srinath Srinivasa, Sujit Kumar. A Platform Based on the Multi-Dimensional Data Model for Analysis of Bio-Molecular Structures. Proc of VLDB 2003, Berlin, Germany.

47. References 5. Xifeng Yan, Jiawei Han. gSpan: Graph-Based Substructure Pattern Mining. 6. Xifeng Yan, Philip S. Yu, Jiawei Han. Graph Indexing: A Frequent Substructure Based Approach. Proc of SIGMOD 2004. 7. Srinath Srinivasa, Martin Meier, Mandar R. Mutalikdesai, Gopinath P.S., Gowrishankar K.A. LWI and Safari: A New Index Structure and Query Model for Graph Databases.

48. Thank You! For more interaction, contact me at [email_address]