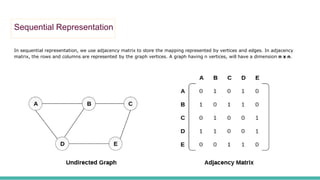
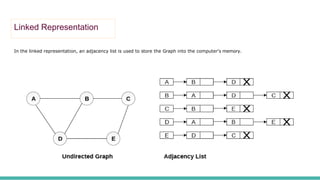
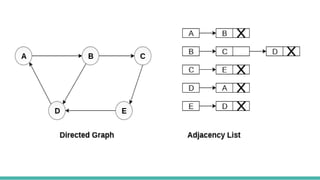
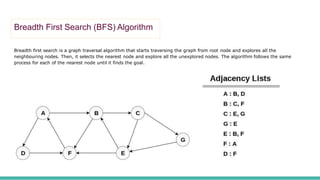
This document discusses graph representations and traversal algorithms. It describes two common ways to represent graphs: sequential representation using an adjacency matrix and linked representation using an adjacency list. It also explains two graph traversal algorithms - breadth-first search (BFS) and depth-first search (DFS). BFS explores all neighboring nodes first before moving to the next level, while DFS goes deeper first before backtracking. Pseudocode is provided to demonstrate the steps of each algorithm.

1. GraphRepresentations
RAMKRISHNA
BHAGAT

2. Contents
●
●
●
Introduction
Applications
Representations
➢ Sequential
➢ Linked
● TraversalAlgorithms

3. Introduction
A graph can be defined as group of vertices and edges that are used to connect these vertices. A graph can be seen as a cyclic
tree, where the vertices (Nodes) maintain any complex relationship among them instead of having parent child relationship.

4. Applications of Graph

5. Representations of graph
❖ Sequential Representation
❖ Linked Representation

6. Sequential Representation
In sequential representation, we use adjacency matrix to store the mapping represented by vertices and edges. In adjacency
matrix, the rows and columns are represented by the graph vertices. A graph having n vertices, will have a dimension n x n.

8. Linked Representation
In the linked representation, an adjacency list is used to store the Graph into the computer's memory.

10. Graph Traversal Algorithm
● Breadth First Search
● Depth First Search

11. Breadth First Search (BFS) Algorithm
Breadth first search is a graph traversal algorithm that starts traversing the graph from root node and explores all the
neighbouring nodes. Then, it selects the nearest node and explore all the unexplored nodes. The algorithm follows the same
process for each of the nearest node until it finds the goal.

12. Steps :
1. AddAtoQUEUE1andNULLtoQUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}
2.DeletetheNodeAfromQUEUE1andinsert all its neighbours.
InsertNodeAinto QUEUE2
QUEUE1 = {A}
QUEUE2 = {NULL}
3.DeletethenodeBfromQUEUE1andinsertall its neighbours.
InsertnodeBinto QUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}

13. :4.DeletethenodeDfromQUEUE1andinsertall its neighbours.
SinceFis theonlyneighbourofit whichhasbeen inserted,
wewill notinsertit again.InsertnodeDintoQUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}
5.DeletethenodeCfromQUEUE1andinsertall its neighbours.
AddnodeCtoQUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}
6.RemoveFfromQUEUE1andaddall its neighbours.Sinceall ofits neighbours
hasalready beenadded,wewill notaddthemagain.AddnodeFtoQUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}

14. 7. RemoveEfromQUEUE1,all ofE'sneighbourshasalready beenadded to
QUEUE1thereforewewill notaddthemagain.Allthenodesarevisited
andthetarget nodei.e.Eis encounteredintoQUEUE2.
QUEUE1 = {A}
QUEUE2 = {NULL}
Now, backtrack from E to A, using the nodes available in QUEUE2.
The minimum path will be A → B → C → E.

15. Depth First Search (BFS) Algorithm
Depth first search (DFS) algorithm starts with the initial node of the graph G, and then goes to deeper and deeper until we find
the goal node or the node which has no children. The algorithm, then backtracks from the dead end towards the most recent node
that is yet to be completely unexplored.

16. Steps :
1. PushHontothe Stack.
QUEUE1 = {A}
QUEUE2 = {NULL}
2.POPthetopelementofthestack i.e. H,printit andpushall the
neighboursofHontothestack that areis ready state.
QUEUE1 = {A}
QUEUE2 = {NULL}
3.Popthetopelementofthestack i.e.A,printit andpushall the
neighboursofAontothestack thatareinready state
QUEUE1 = {A}
QUEUE2 = {NULL}

17. :4.Popthetopelementofthestack i.e.D,printit andpushall theneighbours
ofDontothestack that areinready state.
QUEUE1 = {A}
QUEUE2 = {NULL}
5.Popthetopelementofthestack i.e.F,printit andpushall theneighbours
ofFontothestack that areinready state.
QUEUE1 = {A}
QUEUE2 = {NULL}
6.Pop the top of the stack i.e.Band pushall the neighbours
QUEUE1 = {A}
QUEUE2 = {NULL}

18. :
7. Popthetopofthestack i.e.Candpushall theneighbours.
QUEUE1 = {A}
QUEUE2 = {NULL}
8.Popthetopofthestack i.e.Gandpushall its neighbours.
QUEUE1 = {A}
QUEUE2 = {NULL}
9.Pop the top of the stack i.e.Eand pushall its neighbours.
QUEUE1 = {A}
QUEUE2 = {NULL}

19. Hence, the stack now becomes empty and all the nodes of the graph have been traversed.
The printing sequence of the graph will be :
H → A → D → F → B → C → G → E

20. Thank You….