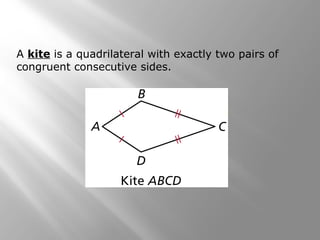
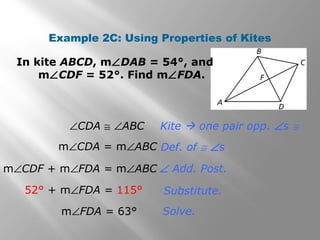
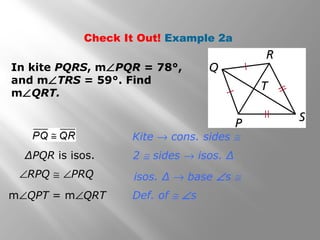
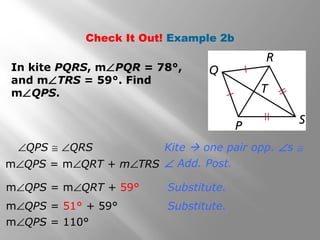
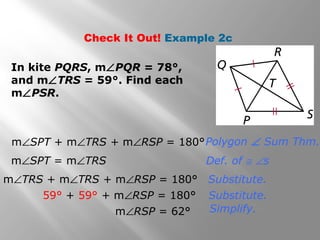
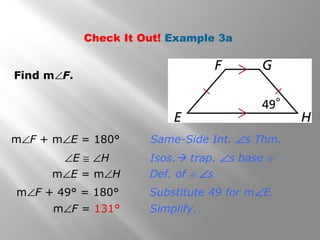
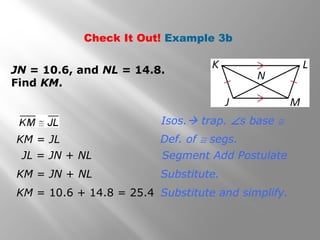
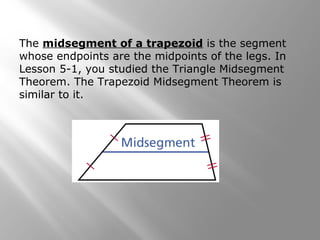
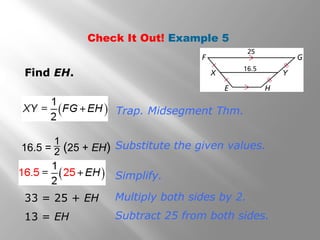
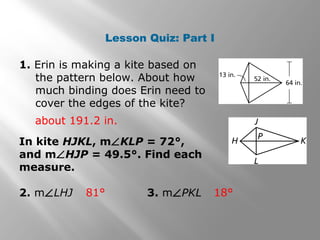
This document provides information about properties of kites and trapezoids. It includes examples of using properties of kites to solve problems involving finding missing angle measures. Examples also demonstrate using properties of isosceles trapezoids, such as the fact that base angles are congruent and legs are congruent. The document concludes with the trapezoid midsegment theorem and examples applying it to find missing segment lengths.

1. UUNNIITT 66..66 TTRRAAPPEEZZOOIIDDSS AANNDD KKIITTEESS

2. Poperties of Kites and Trapezoids
Warm Up
Solve for x.
1. x2 + 38 = 3x2 – 12
2. 137 + x = 180
3.
4. Find FE.
5 or –5
43
156

3. Objectives
Use properties of kites to solve
problems.
Use properties of trapezoids to solve
problems.

4. Vocabulary
kite
trapezoid
base of a trapezoid
leg of a trapezoid
base angle of a trapezoid
isosceles trapezoid
midsegment of a trapezoid

5. A kite is a quadrilateral with exactly two pairs of
congruent consecutive sides.

7. Example 1: Problem-Solving Application
Lucy is framing a kite with
wooden dowels. She uses two
dowels that measure 18 cm,
one dowel that measures 30
cm, and two dowels that
measure 27 cm. To complete
the kite, she needs a dowel to
place along . She has a dowel
that is 36 cm long. About how
much wood will she have left
after cutting the last dowel?

8. Example 1 Continued
11 Understand the Problem
The answer will be the amount of wood Lucy has
left after cutting the dowel.
22 Make a Plan
The diagonals of a kite are perpendicular, so the
four triangles are right triangles. Let N represent the
intersection of the diagonals. Use the Pythagorean
Theorem and the properties of kites to find ,
and . Add these lengths to find the length of .

9. 33 Solve
Example 1 Continued
N bisects JM.
Pythagorean Thm.
Pythagorean Thm.

10. Example 1 Continued
Lucy needs to cut the dowel to be 32.4 cm long.
The amount of wood that will remain after the
cut is,
36 – 32.4 » 3.6 cm
Lucy will have 3.6 cm of wood left over after the
cut.

11. Example 1 Continued
44 Look Back
To estimate the length of the diagonal, change the
side length into decimals and round. , and
. The length of the diagonal is
approximately 10 + 22 = 32. So the wood
remaining is approximately 36 – 32 = 4. So 3.6 is a
reasonable answer.

12. Check It Out! Example 1
What if...? Daryl is going to make
a kite by doubling all the measures
in the kite. What is the total
amount of binding needed to cover
the edges of his kite? How many
packages of binding must Daryl
buy?

13. Check It Out! Example 1 Continued
11 Understand the Problem
The answer has two parts.
• the total length of binding Daryl needs
• the number of packages of binding Daryl must
buy

14. Check It Out! Example 1 Continued
22 Make a Plan
The diagonals of a kite are perpendicular, so the
four triangles are right triangles. Use the
Pythagorean Theorem and the properties of
kites to find the unknown side lengths. Add
these lengths to find the perimeter of the kite.

15. Check It Out! Example 1 Continued
33 Solve
Pyth. Thm.
Pyth. Thm.
perimeter of PQRS =

16. Check It Out! Example 1 Continued
Daryl needs approximately 191.3 inches of binding.
One package of binding contains 2 yards, or 72 inches.
packages of binding
In order to have enough, Daryl must buy 3 packages
of binding.

17. Check It Out! Example 1 Continued
44 Look Back
To estimate the perimeter, change the side lengths
into decimals and round.
, and . The perimeter of the
kite is approximately
2(54) + 2 (41) = 190. So 191.3 is a reasonable
answer.

18. Example 2A: Using Properties of Kites
In kite ABCD, mÐDAB = 54°, and
mÐCDF = 52°. Find mÐBCD.
Kite  cons. sides @
ΔBCD is isos. 2 @ sides isos. Δ
isos. Δ base Ðs @
Def. of @ Ð s
Polygon Ð Sum Thm.
ÐCBF @ ÐCDF
mÐCBF = mÐCDF
mÐBCD + mÐCBF + mÐCDF = 180°

19. Example 2A Continued
Substitute mÐCDF
for mÐCBF.
Substitute 52 for
mÐCBF.
Subtract 104
from both sides.
mÐBCD + mÐCBF + mÐCDF = 180°
mÐBCD + mÐCBF + mÐCDF = 180°
mÐBCD + 52° + 52° = 180°
mÐBCD = 76°

20. Example 2B: Using Properties of Kites
In kite ABCD, mÐDAB = 54°, and
mÐCDF = 52°. Find mÐABC.
Kite  one pair opp. Ðs @
Def. of @ Ðs
Polygon Ð Sum Thm.
ÐADC @ ÐABC
mÐADC = mÐABC
mÐABC + mÐBCD + mÐADC + mÐDAB = 360°
Substitute mÐABC for mÐADC.
mÐABC + mÐBCD + mÐABC + mÐDAB = 360°

21. Example 2B Continued
mÐABC + mÐBCD + mÐABC + mÐDAB = 360°
mÐABC + 76° + mÐABC + 54° = 360°
Substitute.
Simplify.
2mÐABC = 230°
mÐABC = 115° Solve.

22. Example 2C: Using Properties of Kites
In kite ABCD, mÐDAB = 54°, and
mÐCDF = 52°. Find mÐFDA.
Kite  one pair opp. Ðs @
Def. of @ Ðs
Ð Add. Post.
Substitute.
Solve.
ÐCDA @ ÐABC
mÐCDA = mÐABC
mÐCDF + mÐFDA = mÐABC
52° + mÐFDA = 115°
mÐFDA = 63°

23. Check It Out! Example 2a
In kite PQRS, mÐPQR = 78°,
and mÐTRS = 59°. Find
mÐQRT.
Kite ® cons. sides @
ΔPQR is isos. 2 @ sides ® isos. Δ
isos. Δ ® base Ðs @
Def. of @ Ðs
ÐRPQ @ ÐPRQ
mÐQPT = mÐQRT

24. Check It Out! Example 2a Continued
Polygon Ð Sum Thm.
Substitute 78 for
mÐPQR.
mÐPQR + mÐQRP + mÐQPR = 180°
78° + mÐQRT + mÐQPT = 180°
78° + mÐQRT + mÐQRT = 180° Substitute.
78° + 2mÐQRT = 180°
2mÐQRT = 102°
mÐQRT = 51°
Substitute.
Subtract 78 from
both sides.
Divide by 2.

25. Check It Out! Example 2b
In kite PQRS, mÐPQR = 78°,
and mÐTRS = 59°. Find
mÐQPS.
Kite  one pair opp. Ðs @
Ð Add. Post.
Substitute.
Substitute.
ÐQPS @ ÐQRS
mÐQPS = mÐQRT + mÐTRS
mÐQPS = mÐQRT + 59°
mÐQPS = 51° + 59°
mÐQPS = 110°

26. Check It Out! Example 2c
Polygon Ð Sum Thm.
Def. of @ Ðs
Substitute.
Substitute.
Simplify.
In kite PQRS, mÐPQR = 78°,
and mÐTRS = 59°. Find each
mÐPSR.
mÐSPT + mÐTRS + mÐRSP = 180°
mÐSPT = mÐTRS
mÐTRS + mÐTRS + mÐRSP = 180°
59° + 59° + mÐRSP = 180°
mÐRSP = 62°

27. A trapezoid is a quadrilateral with exactly one pair of
parallel sides. Each of the parallel sides is called a
base. The nonparallel sides are called legs. Base
angles of a trapezoid are two consecutive angles
whose common side is a base.

28. If the legs of a trapezoid are congruent, the trapezoid
is an isosceles trapezoid. The following theorems
state the properties of an isosceles trapezoid.

30. Reading Math
Theorem 6-6-5 is a biconditional statement. So it
is true both “forward” and “backward.”

31. Example 3A: Using Properties of Isosceles
Trapezoids
Isos. trap. Ðs base @
Find mÐA.
Same-Side Int. Ðs Thm.
Substitute 100 for mÐC.
Subtract 100 from both sides.
Def. of @ Ðs
Substitute 80 for mÐB
mÐC + mÐB = 180°
100 + mÐB = 180
mÐB = 80°
ÐA @ ÐB
mÐA = mÐB
mÐA = 80°

32. Example 3B: Using Properties of Isosceles
Trapezoids
KB = 21.9m and MF = 32.7.
Find FB.
Isos.  trap. Ðs base @
Def. of @ segs.
Substitute 32.7 for FM.
Seg. Add. Post.
Substitute 21.9 for KB and 32.7 for KJ.
Subtract 21.9 from both sides.
KJ = FM
KJ = 32.7
KB + BJ = KJ
21.9 + BJ = 32.7
BJ = 10.8

33. Example 3B Continued
Same line.
Isos. trap.  Ðs base @
Isos. trap.  legs @
SAS
CPCTC
Vert. Ðs @
ÐKFJ @ ÐMJF
ΔFKJ @ ΔJMF
ÐBKF @ ÐBMJ
ÐFBK @ ÐJBM

34. Example 3B Continued
Isos. trap.  legs @
AAS
CPCTC
Def. of @ segs.
Substitute 10.8 for JB.
ΔFBK @ ΔJBM
FB = JB
FB = 10.8

35. Check It Out! Example 3a
Same-Side Int. Ðs Thm.
Isos. trap. Ðs base @
Def. of @ Ðs
Substitute 49 for mÐE.
mÐF + mÐE = 180°
ÐE @ ÐH
mÐE = mÐH
mÐF + 49° = 180°
mÐF = 131°
Simplify.
Find mÐF.

36. Check It Out! Example 3b
JN = 10.6, and NL = 14.8.
Find KM.
Isos. trap. Ðs base @
Def. of @ segs.
Segment Add Postulate
Substitute.
Substitute and simplify.
KM = JL
JL = JN + NL
KM = JN + NL
KM = 10.6 + 14.8 = 25.4

37. Example 4A: Applying Conditions for Isosceles
Trapezoids
Find the value of a so that PQRS
is isosceles.
a = 9 or a = –9
Trap. with pair base
Ðs  @ isosc. trap.
Def. of @ Ðs
Substitute 2a2 – 54 for mÐS and
a2 + 27 for mÐP.
Subtract a2 from both sides and add
54 to both sides.
Find the square root of both sides.
ÐS @ ÐP
mÐS = mÐP
2a2 – 54 = a2 + 27
a2 = 81

38. Example 4B: Applying Conditions for Isosceles
Trapezoids
AD = 12x – 11, and BC = 9x – 2. Find
the value of x so that ABCD is
isosceles.
Diags.  @ isosc. trap.
Def. of @ segs.
Substitute 12x – 11 for AD and
9x – 2 for BC.
Subtract 9x from both sides and add
11 to both sides.
Divide both sides by 3.
AD = BC
12x – 11 = 9x – 2
3x = 9
x = 3

39. Check It Out! Example 4
Find the value of x so that
PQST is isosceles.
Trap. with pair base
ÐQ @ ÐS Ðs  @ isosc. trap.
Def. of @ Ðs
Substitute 2x2 + 19 for mÐQ
and 4x2 – 13 for mÐS.
Subtract 2x2 and add
13 to both sides.
mÐQ = mÐS
2x2 + 19 = 4x2 – 13
32 = 2x2
x = 4 or x = –4 Divide by 2 and simplify.

40. The midsegment of a trapezoid is the segment
whose endpoints are the midpoints of the legs. In
Lesson 5-1, you studied the Triangle Midsegment
Theorem. The Trapezoid Midsegment Theorem is
similar to it.

42. Example 5: Finding Lengths Using Midsegments
Find EF.
Trap. Midsegment Thm.
Substitute the given values.
EF = 10.75 Solve.

43. Check It Out! Example 5
Find EH.
Trap. Midsegment Thm.
Substitute the given values.
Simplify.
16.5 = 1 (25 + EH) 2
33 = 25 + EH Multiply both sides by 2.
13 = EH Subtract 25 from both sides.

44. Lesson Quiz: Part I
1. Erin is making a kite based on
the pattern below. About how
much binding does Erin need to
cover the edges of the kite?
about 191.2 in.
In kite HJKL, mÐKLP = 72°,
and mÐHJP = 49.5°. Find each
measure.
2. mÐLHJ 3. mÐPKL
81° 18°

45. Lesson Quiz: Part II
Use the diagram for Items 4 and 5.
4. mÐWZY = 61°. Find mÐWXY.
119°
5. XV = 4.6, and WY = 14.2. Find VZ.
9.6
6. Find LP.
18

46. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.