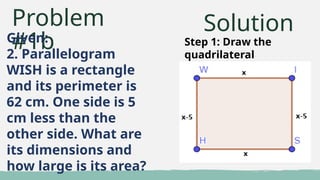
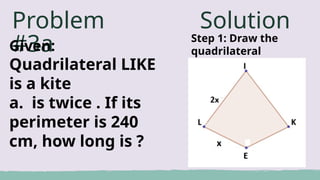
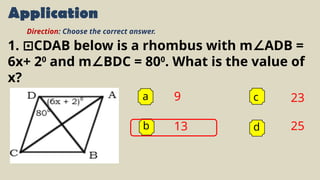
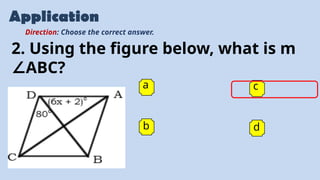
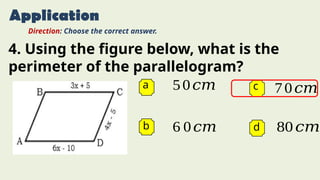
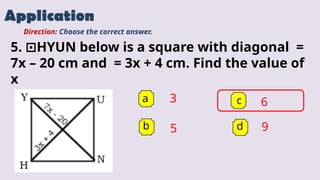
The document provides an overview of solving problems related to parallelograms, trapezoids, and kites, detailing various properties and theorems relevant to these shapes. It includes multiple practice problems with step-by-step solutions and tips for analysis. Additionally, there are applications with multiple-choice questions to test understanding of the concepts presented.

1. PROBLEMS
INVOLVING
PARALLELOGRAM,
TRAPEZOID AND

2. OBJECTIV
ES
1. Analyze
problems
involving
parallelog
rams,
trapezoids
and kites
2. Applies tips to
consider in
solving problems
involving
parallelograms,
trapezoids and
kites
3. Show
accuracy in
solving problem
involving
parallelograms,
trapezoid and
kites

3. Step 1 Step 2 Step 3
Boy or Girl
Choose Boy
If the answer
is FALSE
Choose Girl
if the answer
is TRUE
If your answer is
correct, you may
take your seat,
but if your
answer is wrong,
please remain
standing until
your classmate
save you!

4. 1. If a quadrilateral is an
isosceles trapezoid, then the
diagonals are congruent.
TRUE

5. 2. If a quadrilateral is an isosceles
trapezoid, then the consecutive
angles are supplementary.
FALSE

6. 3. An isosceles trapezoid is a
trapezoid with congruent
bases.
FALSE

7. 4. If a quadrilateral is a kite, then
it has one diagonal that bisects a
pair of opposite angles.
TRUE

8. 5. If a quadrilateral is a kite, then
its area is half the product of the
lengths of its diagonals.
TRUE

9. PROBLEMS
INVOLVING
PARALLELOGRAM,
TRAPEZOID AND

10. Tips to consider in solving problems
involving parallelograms, trapezoids and
kites:
1.Draw the quadrilateral with the given
values.
2.Analyze the problem (Think of all the
properties and theorems that could be
helpful in solving the problem).
3.Solve the problem.

11. Problem
#1a
Given:
1. Quadrilateral
WISH is a
parallelogram.
a. If m W = x + 15
∠
and m S = 2x + 5,
∠
what is m W?
∠
Solution
Step 1: Draw the
quadrilateral

12. The relationship between
∠W and S in
∠
parallelogram WISH is
that they are congruent
as they are opposite
angles. Equate the two
expressions to solve for x
and eventually the
measure of W.
∠
Step 3: Solve
the Problem
x + 15 = 2x + 5
15 – 5 = 2x - x
x = 10
Therefore,
m W = x + 15
∠
= 10 + 15
= 25o
Step 2: Analyze
the Problem

13. Problem
#1b
Given:
2. Parallelogram
WISH is a rectangle
and its perimeter is
62 cm. One side is 5
cm less than the
other side. What are
its dimensions and
how large is its area?
Solution
Step 1: Draw the
quadrilateral

14. Since it’s a rectangle, let x be
the longer side and x-5 the
other side and the opposite
sides are congruent. To find
the value of x and eventually
the dimensions, use the
formula in finding the
perimeter as this is already
given. Then, find the area
(A=LW) .
Step 3: Solve
the Problem
Step 2: Analyze
the Problem
𝑃 = 2( + )
𝐿 𝑊
62 = 2 (x – 5 + x)
62 = 2(2x - 5)
62 = 4 10
𝑥 −
62 + 10 = 4𝑥
72 = 4𝑥
= x
x = 𝟏𝟖

15. Step 3: Solve
the Problem
𝑃 = 2( + )
𝐿 𝑊
62 = 2 (x – 5 + x)
62 = 2(2x - 5)
62 = 4 10
𝑥 −
62 + 10 = 4𝑥
72 = 4𝑥
= x
x = 𝟏𝟖
Therefore,
the width(x) is
18cm, length(x-5)
is 13cm and the
area(L times
width) is 234 cm2
.

16. Problem
#2a
Given:
1. Quadrilateral POST is
an isosceles trapezoid
and ER is its midline.
a. If ST = 2x, PO = x-5
and ER = 38cm, how
long is each base?
Solution
Step 1: Draw the
quadrilateral

17. To find the value of
x, we need to use the
equation in finding
the midline of a
trapezoid.
ER =
Step 3: Solve
the Problem
Step 2: Analyze
the Problem
ER =
38 =
76 = 3x - 5
76 + 5 = 3x
81 = 3x
x =
x = 27

18. Step 3: Solve the
Problem ER =
38 =
76 = 3x - 5
76 + 5 = 3x
81 = 3x
x =
x = 27
Therefore, the bases
PO = x – 5
= 27 – 5
= 22 cm
TS = 2x
= 2(27)
= 54 cm

19. Problem
#2b
Given:
If m T = 2x + 5
∠
and m S= 3x-
∠
10, what is m
O?
∠
Solution
Step 1: Draw the
quadrilateral

20. The relationship between
∠T and S in trapezoid POST is that
∠
they are congruent. We need to
equate the given expressions to find
the value of x, eventually the m T and
∠
m O as they are supplementary.
∠
Step 2: Analyze the
Problem

21. Step 3: Solve the
Problem
2 + 5 = 3 10
𝑥 𝑥 −
10 + 5 = 3x-2x
x = 15
∠T = 2x + 5
=2(15) + 5
= 30 + 5
∠T = 35°
∠T + O = 180
∠
35 + O = 180
∠
∠O = 180 35
−
∠O = °
𝟏𝟒𝟓
∠T + O= 180
∠
35° + ° = 180°
𝟏𝟒𝟓

22. Problem
#3a
Given:
Quadrilateral LIKE
is a kite
a. is twice . If its
perimeter is 240
cm, how long is ?
Solution
Step 1: Draw the
quadrilateral

23. The perimeter of the kite will
be used to find the value of x
and eventually the length of .
P = 2 ( + )
Step 2: Analyze the
Problem

24. Step 3: Solve the
Problem
240 = 2(x + 2x)
240 = 2(3x)
240 = 6x
= x
𝒙 = 40
Therefore,
= 2x
= 2(40)
= 80 cm

25. Application
a 9
13
23
25
b
c
d
Direction: Choose the correct answer.
1. CDAB below is a rhombus with m ADB =
⊡ ∠
6x+ 20
and m BDC = 80
∠ 0
. What is the value of
x?

26. Application
a
b
c
d
Direction: Choose the correct answer.
2. Using the figure below, what is m
ABC?
∠

27. Application
a 5 𝑐𝑚
b
c
d
Direction: Choose the correct answer.
3. ABCD below is a parallelogram with = 3x+
⊡
5 cm, = 4x – 5 cm, and = 6x – 10 cm. What is
length of ?
11𝑐𝑚
15𝑐𝑚
20𝑐𝑚

28. Application
a 50𝑐𝑚
b
c
d
Direction: Choose the correct answer.
4. Using the figure below, what is the
perimeter of the parallelogram?
6 0𝑐𝑚
70𝑐𝑚
80𝑐𝑚

29. Application
a 3
b
c
d
Direction: Choose the correct answer.
5. HYUN below is a square with diagonal =
⊡
7x – 20 cm and = 3x + 4 cm. Find the value of
x
5
6
9