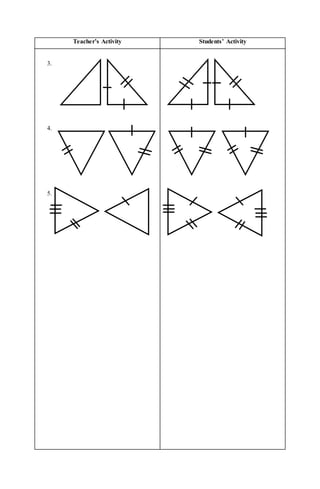
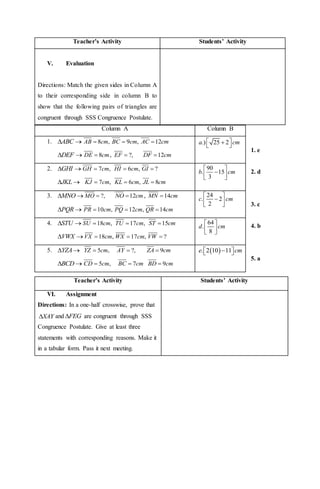
The document outlines a lesson plan for teaching the SSS (Side-Side-Side) congruence postulate in a teacher education department. It includes objectives, procedures, materials needed, and a detailed classroom activity to engage students in understanding triangle congruence through drawing and analysis. The lesson emphasizes the importance of teamwork and cooperation in geometry and real-life applications of congruent triangles.

1. Gov. Alfonso D. Tan College
Teacher Education Department
Maloro, Tangub City
Demonstrator : Elton John B. Embodo
Subject Matter : SSS (Side-Side-Side) Congruence Postulate
Cooperating School : Sta. Maria National High School
Critic Teacher : Mr. Roland B. Amora
Principal : Mrs. Efleda D. Enerio

2. I. Objectives: At the end of the lesson, students are expected to:
a. complete the congruent marks to illustrate that the
triangles are congruent through SSS Congruence
Theorem;
b. match the given sides of triangles to show that the
triangles are congruent through SSS Congruence
Postulate;
c. illustrate the importance of being part of the group by
citing an example.
II. Subject Matter: SSS (Side-Side-Side) Congruence Postulate
Reference: Mathematics Learner’s Module for Grade 8 page (357)
Skills: drawing, analyzing and solving
Values: unity and cooperation
III. Materials: ruler, pencil, bond paper and cardboard
IV. Procedure: 4A’s Method
Teacher’s Activity Students’ Activity
A. Preparation
a. Review
(prayer)
(greetings)
(announcing of classroom rules)
(checking of attendance)
(collecting of assignment)
Before we proceed to our new lesson for today,
let’s have first a review about our lesson last
meeting
What did we discuss last meeting?
Yes Joyce!
Very good!
Who can recall what ASA Congruence
Postulate is?
Yesterday, we discussed about ASA
Congruence Postulate.

3. Teacher’s Activity Students’ Activity
Yes Evan!
Absolutely!
Who wants to go to the board and illustrate the
ASA Congruence Postulate?
Yes Rodan!
Very good!
The ABC and XYZ are congruent since
,A X   AC XZ and C Z   it refers
to ASA Congruence Postulate.
a. Motivation
Now class, I have here two triangles made
from cardboard material. One is colored blue
and the other one is colored yellow.
Class, do you know on how to determine that
these two triangles colored blue and colored
yellow are congruent by dealing only on their
sides not the angles?
ASA Congruence Postulate states that, “If the
two angles and the included side of one
triangle are congruent to the corresponding two
angles and the included side of another
triangle, then the triangles are congruent.
(student does as told)
No, Sir!
A
B
C
X
Y Z

4. Teacher’s Activity Students’ Activity
B. Activity
So be with me this morning as I’ll discuss to
you the “SSS Congruence Postulate.”
Everybody read!
a. Statement of the Aim
*complete the congruent marks to illustrate
that the triangles are congruent through SSS
Congruence Postulate;
*match the given sides of triangles to show
that the triangles are congruent through SSS
Congruence Postulate;
*illustrate the importance of being part of a
group by citing an example.
Now, I’ll group you into 4 groups and form a
circle with your group. All you have to do
class is to draw the desired figure through the
following procedures being flashed on the
screen.
Do you get me class?
When you are already finished, you have to say
with action, “Clap, clap, clap Champion”! The
group which can finish first will be the winner
and will receive a secret price.
I’ll give you five minutes to do it and your
time will start now.
“SSS Congruence Postulate”
Yes Sir.
Students do as told.

5. Teacher’s Activity Students’ Activity
C. Analysis
I want somebody from the group 1 to draw
their figure on the board.
Yes Lovely
Somebody from the group 2 to draw their
figure on the board.
Yes Apple
Any representative from the group 3 to discuss
the work of group 1.
Yes Adrian
Any representative from the group 4 to discuss
the work of the group 2.
Yes Rodan
Very good!
Let’s name the other triangle as OMN .
Do the following in your group:
(student does as told)
(student does as told)
(student does as told)
(student does as told)
1. Draw a straight horizontal
line segment and name it as
ST having a length of
15cm.
2. On the Point S of the line
segmentST , draw a
vertical line segment and
name it as SU having a
length of 20cm.
3. Connect the point U and T
to form a new diagonal line
segment named UT having
a measure of 25cm.
4. Name the newly formed
triangle as STU and
indicate the measures of the
three sides of STU .

6. Teacher’s Activity Students’ Activity
What side of STU that corresponds to the
side MO of MNO ?
Yes Aaron
Very good!
Since the two sides are corresponding, then
what have you observed about their measures?
Yes Cheyenne
That’s right
When they have the same measures, what are
we going to call them?
Yes Annie
That’s correct
What side of STU that corresponds to the
side MN of MNO ?
Yes Sunshine
Very good!
How are you going to describe the two sides:
MN and ST .
Yes Panfy
Exactly!
How are you going to describe the last pair of
sides; UT and NO?
It is the side SU .
SU and MO have the same measures.
The two sides are congruent.
It is the side ST .
MN and ST are corresponding and congruent
because they have the same measures.
U
S
T
O
M N
20cm20cm
25cm
25cm
15cm 15cm

7. Teacher’s Activity Students’ Activity
Yes Ellajane
Absolutely!
D. Abstraction
Based on the information, can we now
determine that the STU and MNO are
congruent?
Then, why did you say “yes”?
Any idea?
Yes Evan!
Amazing!
Based on Evan’s answer, how are you going to
state the SSS (Side-Side-Side) Congruence
Postulate?
Exactly!
What else?
Yes Sunshine
Very good!
UT and NO are corresponding and they are also
congruent because they have the same
measures which are both 25cm.
Yes Sir
We can now determine that the STU and
MNO are congruent because the three sides
of STU are corresponding and congruent to
the three sides of MNO .
SSS Congruence Postulate
If the three sides of a traingle are
conrresponding and congruent to the three
sides of the other triangle, th the two triangles
are congruent.
SSS Congruence Postulate
If the three sides of a traingle are congruent to
the three sides of another triangle, then they are
congruent.

8. Teacher’s Activity Students’ Activity
For your better understanding, here is now the
exact statement for SSS Congruence Postulate.
Everybody read!
Values Integration
In a triangle, there are three are three sides,
they serve as a group, what if one of the three
sides is missing, can we still form a triangle?
That’s right; we cannot form a triangle with the
two sides left. They should be complete.
In real life situation class, how would you
value a certain member in your group?
Yes Arnie Glenn!
SSS (Side-Side-Side) Congruence Postulate
If the three sides of one triangle are congruent
to the corresponding three sides of another
triangle, then the triangles are conguent.
Example:
IfOT UN ,OS PN and ST UP then
OST PNU   .
No sir
In a group, each memeber has an important
role or function so if one member will be
missing then a group cannot fucntion well.
Example in a certain band, if the vocalist or
guitarist will be missing then that certain
cannot perform well because they are not
T
S
O N
P
U

9. Teacher’s Activity Students’ Activity
Absolutely!
E. Application
How important are congruent triangles in real
world class? How are they being applied?
Yes Evan!
Amazing!
What a nice answer!
Activity 1
Directions: Complete the congruent marks of
the following pairs of triangles to illustrate that
they are congruent through SSS Congruence
Postulate.
1.
2.
complete. So they should value each member,
they should have unity and cooperation within
their group.
Traingles are ver important since they are
useful in constructing geometric structures like
bridges, houses, hospitals, buildings and other
establishements that involve triagles. They
served as the basic foundation to make the
structures strong, balance and safe.

10. Teacher’s Activity Students’ Activity
3.
4.
5.

11. 1. e
2. d
3. c
4. b
5. a
Teacher’s Activity Students’ Activity
VI. Assignment
Directions: In a one-half crosswise, prove that
XAY and FEG are congruent through SSS
Congruence Postulate. Give at least three
statements with corresponding reasons. Make it
in a tabular form. Pass it next meeting.
Teacher’s Activity Students’ Activity
V. Evaluation
Directions: Match the given sides in Column A
to their corresponding side in column B to
show that the following pairs of triangles are
congruent through SSS Congruence Postulate.
Column A Column B
1. ABC  8 ,AB cm 9 ,BC cm 12AC cm
DEF  8DE cm , ?,EF  12DF cm
.) 25 2a cm  
2. GHI  7 ,GH cm 6 ,HI cm ?GI 
JKL  7 ,KJ cm 6 ,KL cm 8JL cm
90
. 15
3
b cm
 
  
3. MNO  ?,MO  12NO cm , 14MN cm
PQR  10 ,PR cm 12 ,PQ cm 14QR cm
24
. 2
2
c cm
 
  
4. STU  18 ,SU cm 17 ,TU cm 15ST cm
VWX  18 ,VX cm 17 ,WX cm ?VW 
64
.
8
d cm
 
  
5. YZA  5 ,YZ cm ?,AY  9ZA cm
BCD  5 ,CD cm 7BC cm 9BD cm
 . 2 10 11e cm  