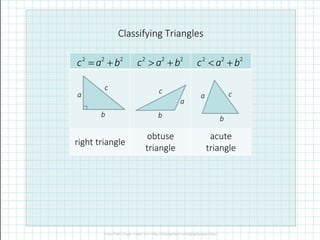
This document discusses classifying triangles using Pythagorean theorem and inequalities. It states that if a2 + b2 = c2, the triangle is right. If a2 + b2 > c2, the triangle is obtuse, and if a2 + b2 < c2, the triangle is acute. Examples are then given to classify triangles as right, obtuse or acute based on their side lengths.

1. 6.3 More Classifying Triangles
The student is able to (I can):
• Use Pythagorean inequalities to classify triangles.

2. Converse of the Pythagorean Theorem
If a2 + b2 = c2, then the triangle is a right triangle.
Another way to think of this is
Pythagorean Inequalities Theorem
If then the triangle is an obtuseobtuseobtuseobtuse triangle.
If then the triangle is an acuteacuteacuteacute triangle.
2 2 2
,c a b> +
2 2 2
,c a b< +
2 2 2
.c a b= +

3. Classifying Triangles
right triangle
obtuse
triangle
acute
triangle
2 2 2
c a b> + 2 2 2
c a b< +2 2 2
c a b= +
a
b
c
a
b
c
a
b
c

4. Examples
Classify the following triangle measures as right, obtuse, or
acute.
1. 5, 7, 10
2. 30, 16, 34
3. 3.8, 4.1, 5.2

5. Examples
Classify the following triangle measures as right, obtuse, or
acute.
1. 5, 7, 10
102 = 100, 52 + 72 = 74 ObtuseObtuseObtuseObtuse
2. 30, 16, 34
342 = 1156, 162 + 302 = 1156 RightRightRightRight
3. 3.8, 4.1, 5.2
5.22 = 27.04, 3.82 + 4.12 = 31.25 AcuteAcuteAcuteAcute