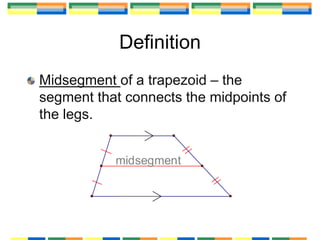
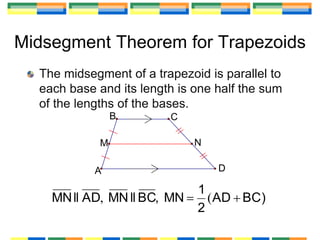
This document defines and discusses properties of trapezoids and kites. It begins by defining a trapezoid as a quadrilateral with one pair of parallel sides, and a kite as a quadrilateral with two pairs of consecutive congruent sides and perpendicular diagonals. The document then presents several theorems about trapezoids and kites, such as: the base angles of an isosceles trapezoid are congruent; the midsegment of a trapezoid is parallel to the bases and half the sum of the base lengths; and the diagonals of a kite are perpendicular and one pair of opposite angles are congruent. Examples demonstrate using these properties to find missing side lengths and angle measures of

1. Trapezoids and Kites

2. Essential Questions
How do I use properties of trapezoids?
How do I use properties of kites?

3. Vocabulary
Trapezoid – a quadrilateral with exactly one
pair of parallel sides.
A trapezoid has two pairs of base angles. In
this example the base angles are A & B
and C & D
A
D C
B
leg leg
base
base

4. Base Angles Trapezoid Theorem
If a trapezoid is isosceles, then each
pair of base angles is congruent.
A
D C
B
 A   B,  C   D

5. Diagonals of a Trapezoid Theorem
A trapezoid is isosceles if and only if its
diagonals are congruent.
A
D C
B
BD
AC
if
only
and
if
isosceles
is
ABCD 

6. Example 1
PQRS is an isosceles trapezoid. Find m P,
m Q and mR.
50
S R
P Q
m R = 50 since base angles are congruent
mP = 130 and mQ = 130 (consecutive angles
of parallel lines cut by a transversal are )

7. Definition
Midsegment of a trapezoid – the
segment that connects the midpoints of
the legs.
midsegment

8. Midsegment Theorem for Trapezoids
The midsegment of a trapezoid is parallel to
each base and its length is one half the sum
of the lengths of the bases.
N
M
A D
B C
BC)
AD
2
1
MN
,
BC
ll
MN
AD
ll
MN (
, 


9. A B
C
D
F G
For trapezoid ABCD, F and G
Are midpoints of the legs.
If AB = 12 and DC = 24,
Find FG.
DC)
AB
2
1
FG ( 

12
24

10. A B
C
D
F G
For trapezoid ABCD, F and G
Are midpoints of the legs.
If AB = 7 and FG = 21,
Find DC.
DC)
AB
2
1
FG ( 

7
21
42 = 12 +DC
30 = DC
Multiply both sides by 2 to get rid of fraction:

11. Definition
Kite – a quadrilateral that has two pairs of
consecutive congruent sides, but opposite
sides are not congruent.

12. Theorem: Perpendicular
Diagonals of a Kite
If a quadrilateral is a kite, then its diagonals
are perpendicular.
D
C
A
B
BD
AC 

13. Theorem:
Opposite Angles of a Kite
If a quadrilateral is a kite, then exactly one
pair of opposite angles are congruent
D
C
A
B
A  C, B  D

14. Example 2
Find the side lengths of the kite.
20
12
12
12
U
W
Z
Y
X

15. Example 2 Continued
WX = 4 34
likewise WZ = 4 34
20
12
12
12
U
W
Z
Y
X
We can use the Pythagorean Theorem to
find the side lengths.
122 + 202 = (WX)2
144 + 400 = (WX)2
544 = (WX)2
122 + 122 = (XY)2
144 + 144 = (XY)2
288 = (XY)2
XY =12 2
likewise ZY =12 2

16. Example 3
Find mG and mJ.
60
132
J
G
H K
Since GHJK is a kite G  J
So 2(mG) + 132 + 60 = 360
2(mG) =168
mG = 84 and mJ = 84

17. Try This!
RSTU is a kite. Find mR, mS and mT.
x
125
x+30
S
U
R T
x +30 + 125 + 125 + x = 360
2x + 280 = 360
2x = 80
x = 40
So mR = 70, mT = 40 and mS = 125
125

18. TEST ON FRIDAY!
QUADRILATERALS!
OH MY!