This document provides information about polygons and quadrilaterals, including:
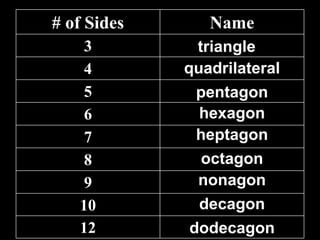
1) It defines different types of polygons based on their number of sides, such as triangles, quadrilaterals, pentagons, etc.
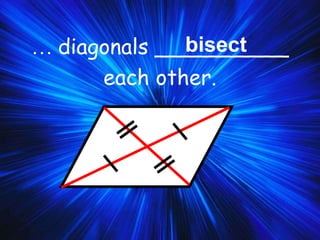
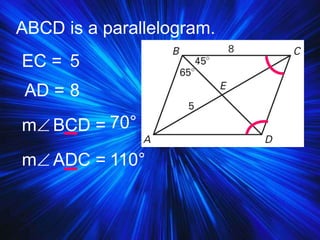
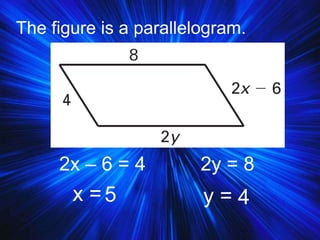
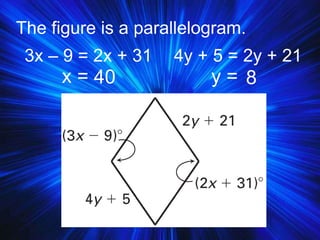
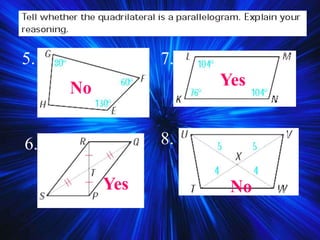
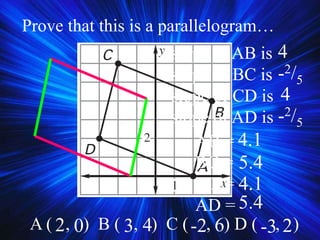
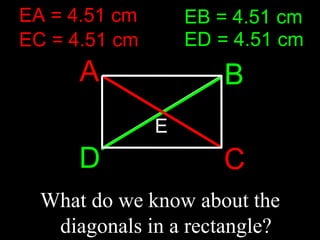
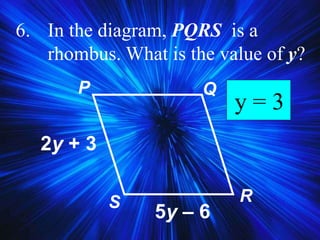
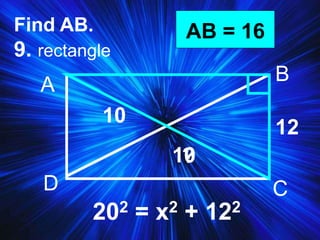
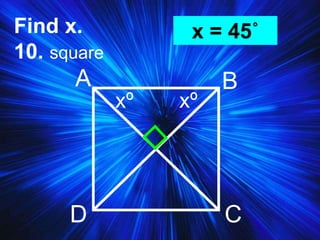
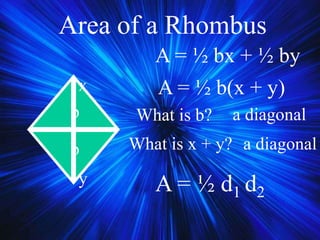
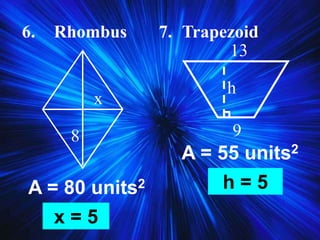
2) It covers properties and theorems about quadrilaterals such as the sum of interior angles of a quadrilateral equaling 360°, properties of parallelograms, and properties of special types of parallelograms like rectangles and squares.
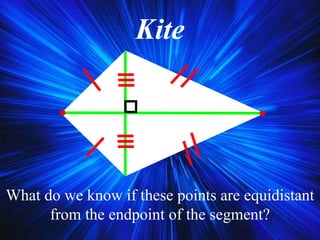
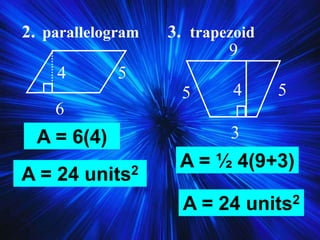
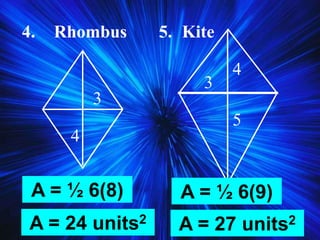
3) It discusses trapezoids and kites, providing their definitions and properties like leg angles of trapezoids being supplementary and diagonals of kites bisecting opposite angles.